Baekjoon Online Judge

algorithm practice

- 단계별 문제풀기

26. 투 포인터

투 포인터 알고리즘과 meet in the middle 알고리즘을 배워 봅시다.

Java / Python

4. 소수의 연속합

1644번

한 쪽에서 두 포인터를 이동시키는 문제 2

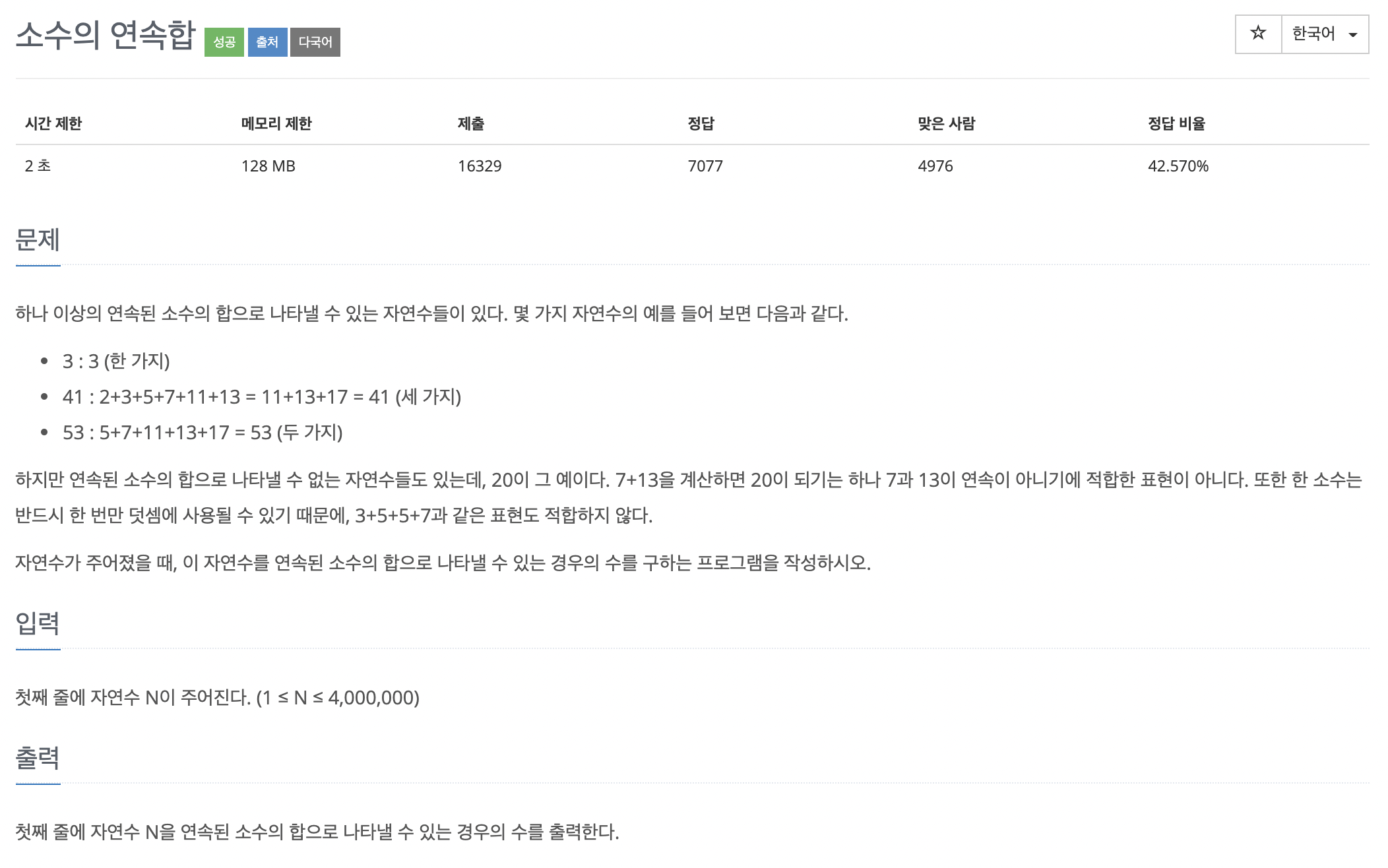
이번 문제는 자연수가 주어졌을 때, 이 자연수를 연속된 소수의 합으로 나타낼 수 있는 경우의 수를 구하는 프로그램을 작성하는 문제입니다.

에라토스테네스의 체를 이용해 소수를 구하고 투 포인터 알고리즘으로 연속되는 합들의 부분합을 확인하는 방식으로 풀었습니다.

• Java

import java.io.*;
import java.util.*;

public class Main {  
	static boolean[] prime;
	static ArrayList<Integer> primeNums = new ArrayList<>();
    
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));   
        
		int N = Integer.parseInt(br.readLine()); 
        
		prime = new boolean[N+1]; 
		prime[0] = prime[1] = true; 
        
		for(int i = 2; i*i <= N; i++){
			if(!prime[i]) {
				for(int j = i*i; j <= N; j += i) 
					prime[j] = true;
			} 
		}
		for(int i = 1; i <= N; i++){
			if(!prime[i]) primeNums.add(i);     
		}
        
		int start = 0, end = 0, sum = 0, cnt = 0;
		while(true){
			if(sum >= N) sum -= primeNums.get(start++);
			else if(end == primeNums.size()) break;
			else sum += primeNums.get(end++);       	
			if(N == sum) cnt++;   
		}
        
		bw.write(cnt + "\n");
        
		bw.flush();
		br.close();
		bw.close();
	}
}

• Python

import sys

N = int(sys.stdin.readline())
primeNums = []
arr = [False, False] + [True] * (N - 1)

for i in range(2, N + 1):
    if arr[i]:
        primeNums.append(i)
    for j in range(i * i, N + 1, i):
        arr[j] = False

start, end, sumN, cnt = 0, 0, 0, 0
        
while True:
    if sumN >= N: 
        if sumN == N:
            cnt += 1
        sumN -= primeNums[start]
        start += 1
    elif end == len(primeNums):
        break
    else:
        sumN += primeNums[end]
        end += 1
        
print(cnt)