Baekjoon Online Judge

algorithm practice

단계별 문제풀기

15. 동적 계획법1

기초적인 동적 계획법 문제들을 풀어봅시다.

Java / Python

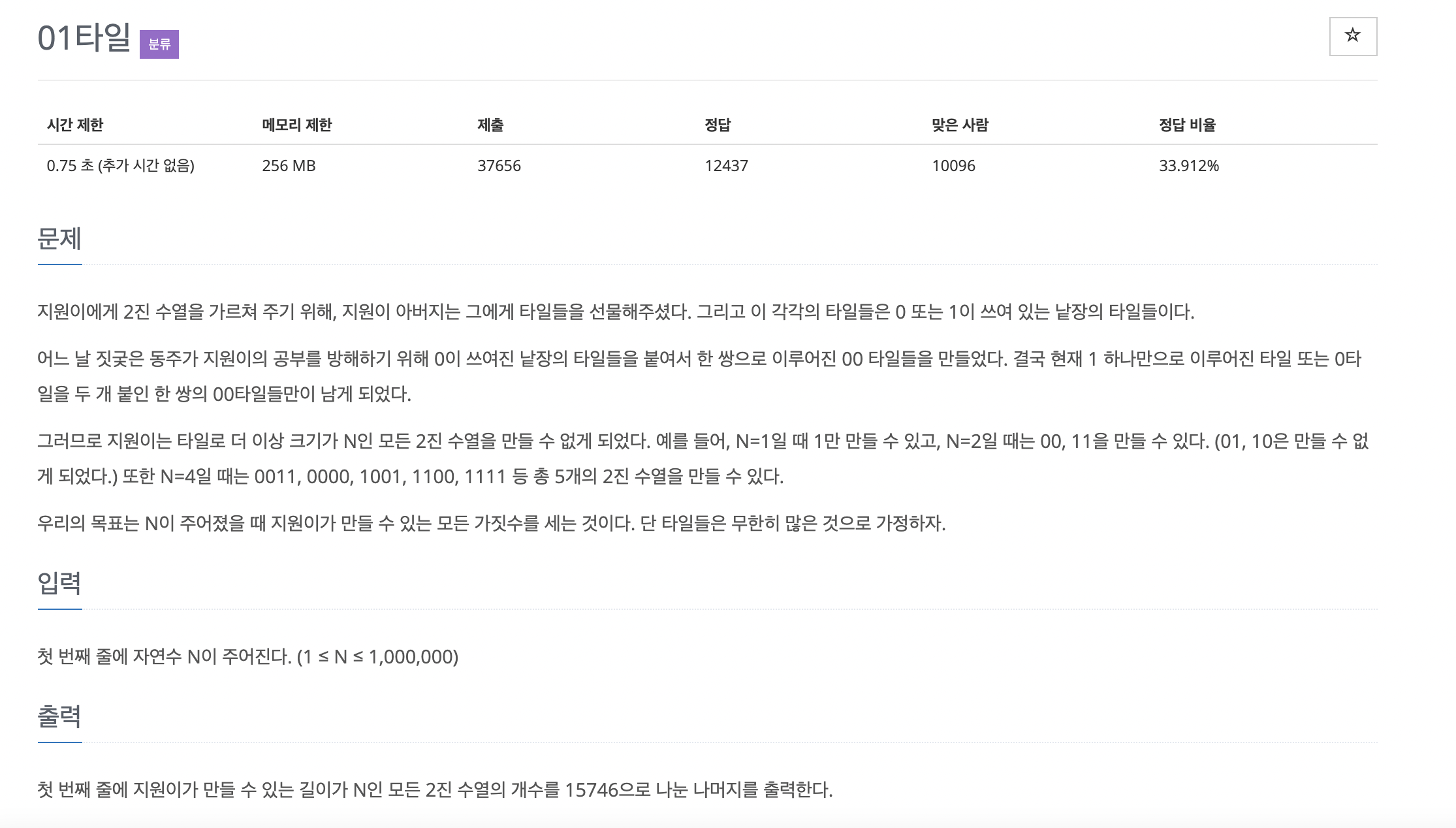
3. 01타일

1904번

점화식의 값을 특정 상수로 나눈 나머지를 구하는 문제

• Java
  
  

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
 
public class Main {
 
	public static int[] dp = new int[1000001];;
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
		int N = Integer.parseInt(br.readLine());
		
		dp[0] = 0;
		dp[1] = 1;
		dp[2] = 2;
 
		for(int i = 3; i < dp.length; i++) {    //비어있을 때 -1
			dp[i] = -1;
		}
		
		System.out.println(Tile(N));
	}
	
	public static int Tile(int N) {
		
		if(dp[N] == -1) {
			dp[N] = (Tile(N - 1) + Tile((N - 2))) % 15746;
		}
		return dp[N];
	}
 
}

• Java ver.2_반복문을 이용한 방법

  앞의 코드가 재귀를 이용한 코드 였다고 하면, 이 방법은 동적 계획법을 변형하여 단순 반복문으로 풀이하는 방법이라고 합니다. N=1, N=2 일 때의 초기 값을 변수로 두고, N이 2보다 큰 값일 경우 반복문을 통해 두 변수를 합해주는 방식으로 작성할 수 있다고 해서 따라 작성해보았습니다..!

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
 
public class Main {
 
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
 
		int N = Integer.parseInt(br.readLine());
 
		System.out.println(Tile(N));
 
	}
 
	public static int Tile(int n) {
         
		int num1 = 1;
		int num2 = 2;
		int sum = 0;
 
		if (n == 1) {
			return 1;
		} 
 
		if (n == 2) {
			return 2;
		}

		for (int i = 2; i < n; i++) {
			sum = (num2 + num1) % 15746;	// 이전 값과 이전의 이전 값의 합 
			num1 = num2;	// 이전의 이전 값은 이전 값으로 변경 
			num2 = sum;		// 이전 값은 현재 합 값으로 변경 
		}
 
		return sum;
	}
}

• Python

import sys 
N = int(sys.stdin.readline()) 
dp = [0] * 1000001 
dp[1] = 1 
dp[2] = 2 

for i in range(3,N+1): 
    dp[i] = (dp[i-1]+ dp[i-2])%15746 
    
print(dp[N])