Baekjoon Online Judge

algorithm practice

단계별 문제풀기

15. 동적 계획법1

기초적인 동적 계획법 문제들을 풀어봅시다.

Java / Python

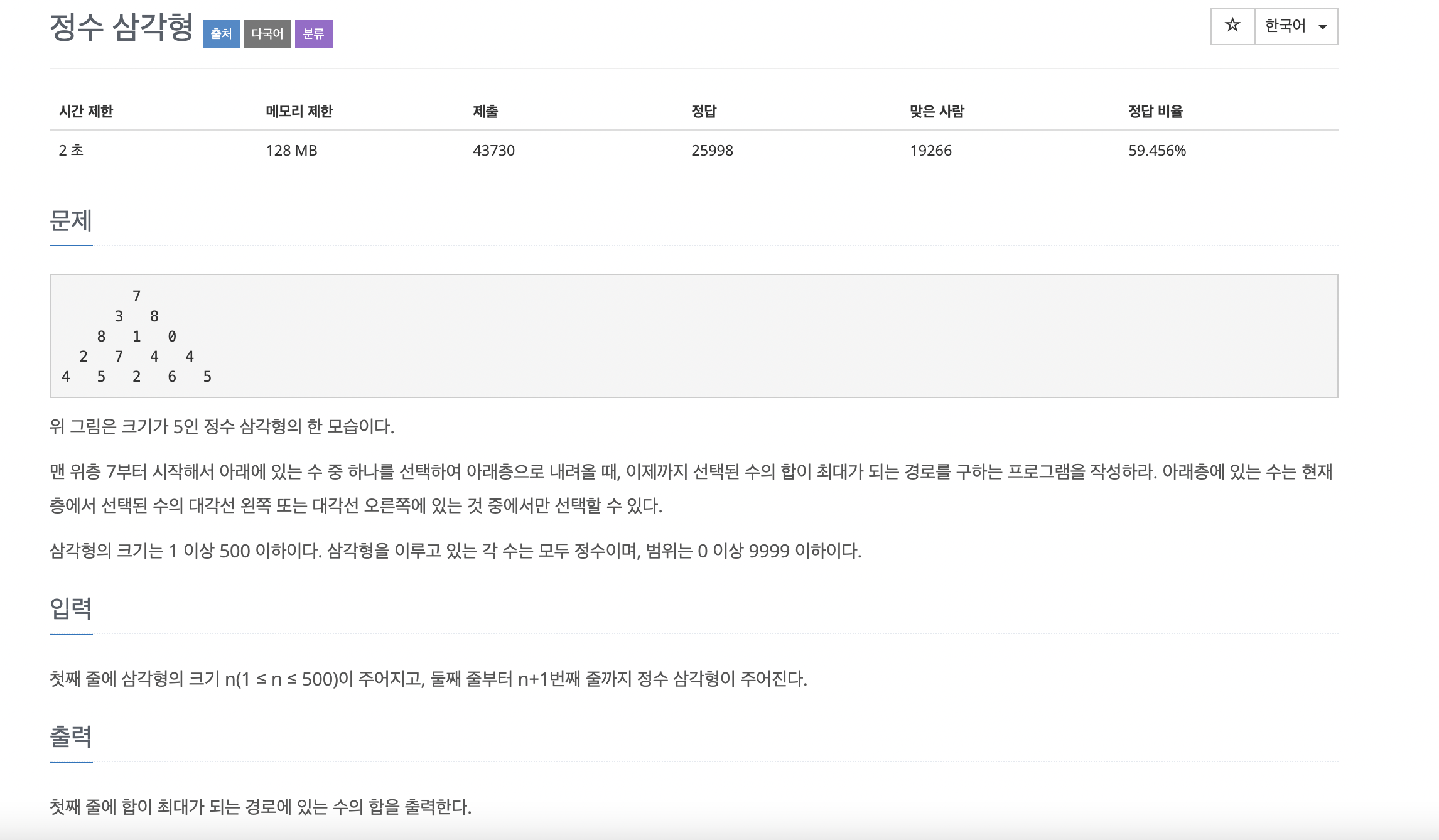
6. 정수 삼각형

1932번

각 층의 모든 칸마다 최댓값을 저장하면서 동적 계획법으로 푸는 문제

• Java

BufferedReader는 문자열을 한 줄로 읽기 때문에, 공백을 기준으로 문자열을 분리하기 위해서 StringTokenizer을 사용했습니다.

DP 배열의 경우 Integer라는 객체를 통해 객체배열로 활용했습니다. int[] 배열로 쓰면 0이라는 값이 default로 초기화가 되는데 문제에서 주어진 값의 범위가 0~9999이기 때문에, 초기값과 저장되는 값으로 0이 겹치게 됩니다. 따라서 객체배열의 default값인 null을 활용하는게 좀 더 편하기 때문에 DP 배열의 경우 Integer[] 배열을 이용하는 분들이 많다고 합니다.

단, Integer[] 배열이 int[] 배열의 4배정도의 메모리가 소모되기 때문에, 재귀가 매우 깊어지거나 입력 값이 많은 경우에는 메모리가 초과될 수 있어서, 객체배열을 피하는게 좋다고 합니다.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
 
public class Main {
 
	static int[][] arr;
	static Integer[][] DP;
	static int N;
 
	public static void main(String[] args) throws IOException {
 
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
 
		N = Integer.parseInt(br.readLine());
 
		arr = new int[N][N];
		DP = new Integer[N][N];
		StringTokenizer st;
        
		// 삼각형 수 입력 받기
		for (int i = 0; i < N; i++) {
			st = new StringTokenizer(br.readLine(), " ");
 
			for (int j = 0; j < i + 1; j++) {
				arr[i][j] = Integer.parseInt(st.nextToken());
			}
		}
        
		// (삼각형) arr 배열의 마지막 행의 값들을 DP의 마지막 행에 똑같이 복사
		for (int i = 0; i < N; i++) {
			DP[N - 1][i] = arr[N - 1][i];
		}
 
		System.out.println(find(0, 0));
 
	}
 
	static int find(int depth, int index) {
		// 마지막 행일 경우 현재 위치 DP값 반환
		if(depth == N - 1) return DP[depth][index];
 
		// 탐색하지 않았던 값이면 다음 행의 양쪽 값 비교
		if (DP[depth][index] == null) {
			DP[depth][index] = Math.max(find(depth + 1, index), find(depth + 1, index + 1)) + arr[depth][index];
		}
		return DP[depth][index];
 
	}
}

• Python

import sys 
T = int(sys.stdin.readline()) 
arr = [list(map(int,sys.stdin.readline().split())) for _ in range(0,T)] 
for i in range(1,T): 
    for j in range(len(arr[i])): 
        if j == 0 : 
            arr[i][j] += (arr[i-1][j]) 
        elif j==i: 
            arr[i][j] +=(arr[i-1][j-1]) 
        else : 
            arr[i][j] += (max(arr[i-1][j],arr[i-1][j-1])) 
print(max(arr[T-1]))