Baekjoon Online Judge

algorithm practice

- 단계별 문제풀기

17. 정수론 및 조합론

정수론과 조합론을 배워 봅시다.

Java / Python

3. 최대공약수와 최소공배수

2609번

최대공약수와 최소공배수를 구하는 문제

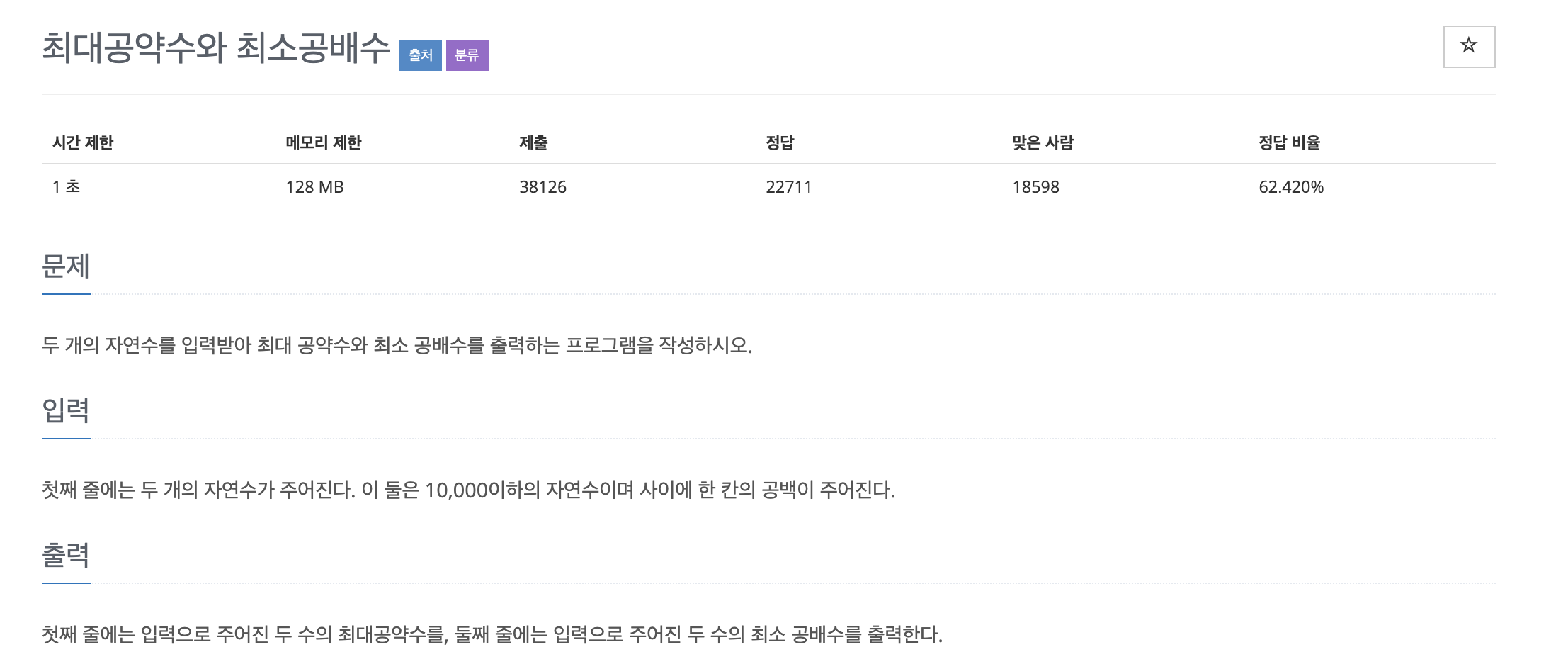
두 개의 자연수를 입력받아 최대 공약수와 최소 공배수를 출력하는 문제입니다.
최대 공약수 GCD를 이용하여 풀 수 있습니다. 조금 더 자세히 정리해보면,
최대 공약수 GCD(Greatest Common Divisor)는 가장 큰 공통된 약수라는 뜻입니다. 최대 공약수를 정확히 구하는 방법은 다음과 같이 정리할 수 있습니다.
"A와 B 두 수가 주어지면 A의 약수들을 모두 구하고, B의 약수들을 모두 구한 뒤 공통 된 약수들만 찾아내어 약수들의 곱으로 다시 나타내준다."
단, 어떤 수가 약수가 매우 많을 경우 인수분해하고 비교해서 곱하는데 시간이 많이 필요로 하게 됩니다. 따라서 '유클리드 호제법' 알고리즘 방식을 많이 사용합니다.
유클리드 호제법 (Euclidean algorithm)이란
2개의 자연수 또는 정식(整式)의 최대공약수를 구하는 알고리즘의 하나이며, 정리는 다음과 같습니다.

• Java

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;

public class Main{
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine(), " ");
        
		int number1 = Integer.parseInt(st.nextToken());
		int number2 = Integer.parseInt(st.nextToken());
		int result1 = gcd(number1, number2);
		
		System.out.println(result1);
		System.out.println(number1 * number2 / result1);
	}
    
	public static int gcd(int n1, int n2){    // 최대 공약수
		if(n2 == 0) return n1;
		return gcd(n2, n1 % n2);
	}
}

• Python

import sys
num1, num2 = map(int, sys.stdin.readline().split())

# gcd
def gcd(n1, n2):
    if n2 == 0 : 
        return n1
    else : 
        return gcd(n2, n1 % n2)
    
result = gcd(num1, num2)
print(result) 
#lcm 
print(num1 * num2 // result)