Baekjoon Online Judge
algorithm practice
- 단계별 문제풀기
37. 강한 연결 요소
Strongly connected component를 다뤄 봅시다.
4. ATM
각각의 SCC를 하나로 묶은 다음 각 묶음마다 답을 계산하는 문제

이번 문제는 출발 장소에서 어떤 레스토랑까지 이동하면서 인출할 수 있는 현금의 최대 액수가 얼마인지를 계산하는 프로그램을 작성하는 문제이다.
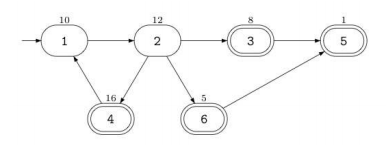
( 예를 들어, 아래 그림처럼 도시에 6개의 교차로가 있다고 하자. 교차로는 원으로 표시되어 있고, 화살표는 도로를 나타낸다. 이중 원으로 표시된 교차로에는 레스토랑이 있다. 각 ATM 기기가 갖고 있는 현금의 액수는 교차로 위에 표시된 숫자이다. 이 예에서 현금 인출을 1번 교차로부터 시작한다면, 반디치는 1-2-4-1-2-3-5의 경로를 통해서 총 47의 현금을 인출할 수 있다. )
SCC를 찾는 알고리즘은 크게 이 두가지 방법이다.
- 타잔 알고리즘
모든 정점에 대해 DFS를 수행하여 SCC를 찾는 알고리즘으로, 코사라주 알고리즘에 비해 적용이 더 쉽다고 한다.
① 인접 정점에 방문하며 자기 자신을 스택에 넣고, 재귀적으로 DFS를 수행한다.
② 인접 정점에 방문했지만, 아직 처리중인 상태일 경우, 작은 값으로 부모값을 갱신한다.
③ 부모 노드의 DFS가 끝난 경우에는, 자신의 id값이 스택에서 나올 때까지 스택에 있는 노드들을 pop하고 scc 배열에 추가한다.
④ 만들어진 하나의 scc를 전체 SCC 배열에 추가한다.
(구현이 더 어렵지만, 활용도는 더 높다고 한다.)
- 코사라주 알고리즘
주어진 방향 그래프의 역방향 그래프와 스택을 사용하여 SCC를 구하는 알고리즘이다. 방향, 역방향 그래프가 동일한 SCC를 구성한다는 것을 이용한 방법이다.
① 주어지는 방향 그래프와 그 그래프의 역방향 그래프를 만든다.
② 정점을 담을 스택을 만들고 임의의 정점부터 DFS를 수행한다.
③ DFS가 끝나는 순서대로 스택에 삽입하고, 아직 방문하지 않은 정점에 대해 DFS를 수행한다.
④ 모든 정점이 스택에 담긴 후에는 스택을 pop하여 나오는 정점부터 역방향 그래프에서 DFS를 수행한다.. 이미 방문한 정점은 pop만 시행한다.
⑤ 이때 탐색되는 모든 정점을 SCC로 묶는다.
이것을 스택이 빌 때까지 진행한다.
(타잔 알고리즘에 비해 구현이 더 쉬운 편이라고 한다.)
저번 문제들과 유사하다. scc를 응용한 문제이며, scc를 구하고 bfs를 이용해서 풀 수 있었다. 조금 더 길고 복잡한 문제이다..
Java / Python
- Java
타잔 알고리즘 이용
import java.io.*;
import java.util.*;
public class Main {
static int scc_total, num;
static ArrayList<Integer>[] edges;
static int[] order, scc_arr;
static boolean[] visit; // SCC 확정된 정점 확인
static Stack<Integer> stack;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken()); // 정점의 개수
int M = Integer.parseInt(st.nextToken()); // 간선의 개수
edges = new ArrayList[N + 1];
for (int i = 0; i < N + 1; i++) {
edges[i] = new ArrayList<>();
}
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
edges[a].add(b);
}
scc_arr = new int[N + 1];
order = new int[N + 1];
visit = new boolean[N + 1];
scc_total = num = 0;
stack = new Stack<>();
for (int i = 0; i < N; i++) {
if (!visit[i])
SCC(i);
}
int[] dp = new int[scc_total];
int[] indegree = new int[scc_total];
List<Integer>[] scc = new ArrayList[scc_total];
for (int i = 0; i < scc_total; i++) {
scc[i] = new ArrayList<>();
}
for (int i = 1; i < N + 1; i++) {
st = new StringTokenizer(br.readLine());
indegree[scc_arr[i]] += Integer.parseInt(st.nextToken());
for (int j : edges[i]) {
if (scc_arr[i] != scc_arr[j])
scc[scc_arr[i]].add(scc_arr[j]);
}
}
st = new StringTokenizer(br.readLine());
int s = scc_arr[Integer.parseInt(st.nextToken())];
int p = Integer.parseInt(st.nextToken());
int answer = 0;
Queue<Integer> que = new LinkedList<Integer>();
dp[s] = indegree[s];
que.add(s);
while (!que.isEmpty()) {
int now = que.poll();
for (int next : scc[now]) {
if (dp[next] < dp[now] + indegree[next]) {
dp[next] = dp[now] + indegree[next];
que.add(next);
}
}
}
st = new StringTokenizer(br.readLine());
while (p-- > 0)
answer = Math.max(answer, dp[scc_arr[Integer.parseInt(st.nextToken())]]);
bw.write(answer + "\n");
bw.flush();
bw.close();
br.close();
}
private static int SCC(int idx) {
order[idx] = ++num;
stack.add(idx);
int root = order[idx];
for (int next : edges[idx]) {
if (order[next] == 0)
root = Math.min(root, SCC(next));
else if (!visit[next])
root = Math.min(root, order[next]);
}
if (root == order[idx]) {
while (true) {
int top = stack.pop();
scc_arr[top] = scc_total;
visit[top] = true;
if (top == idx)
break;
}
scc_total++;
}
return root;
}
}- Python
코사라주 알고리즘 이용 (역방향 그래프 이용)
import sys
from collections import deque
sys.setrecursionlimit(650001)
input = lambda: sys.stdin.readline().rstrip()
read = lambda: map(int, input().split())
def dfs(node):
visit[node] = 1
for now in graph[node]:
if not visit[now]:
dfs(now)
stack.append(node)
def reverse_dfs(node, num):
scc_num[node] = num
scc_arr[num] += 1
scc_val[num] += cash[node]
for now in reverse_graph[node]:
if scc_num[now] == -1:
reverse_dfs(now, num)
elif scc_num[node] != scc_num[now]:
group[scc_num[now]].append(scc_num[node])
N, M = read()
graph = [[] for i in range(N)]
reverse_graph = [[] for i in range(N)]
visit = [0] * N
stack = []
scc_num = [-1] * N
scc_arr = []
group = []
for i in range(M):
a, b = read()
graph[a-1].append(b-1)
reverse_graph[b-1].append(a-1)
cash = [int(input()) for i in range(N)]
for i in range(N):
if not visit[i]:
dfs(i)
scc_val = []
k = 0
while stack:
now = stack.pop()
if scc_num[now] == -1:
group.append([])
scc_arr.append(0)
scc_val.append(0)
reverse_dfs(now, k)
k += 1
S, P = read()
S -= 1
result = list(read())
del graph, reverse_graph
que = deque([scc_num[S]])
dp = [0] * k
dp[scc_num[S]] = scc_val[scc_num[S]]
while que:
now = que.popleft()
for n in group[now]:
if dp[n] < dp[now] + scc_val[n]:
dp[n] = dp[now] + scc_val[n]
que.append(n)
answer = 0
for r in result:
answer = max(answer, dp[scc_num[r-1]])
print(answer)