Baekjoon Online Judge

algorithm practice

- 단계별 문제풀기

29. 유니온 파인드

유니온 파인드(또는 disjoint set, 상호 배타적 집합, ...) 자료구조를 배워 봅시다.

Java / Python

3. 친구 네트워크

4195번

유니온 파인드에 집합의 크기를 구하는 기능을 넣는 문제

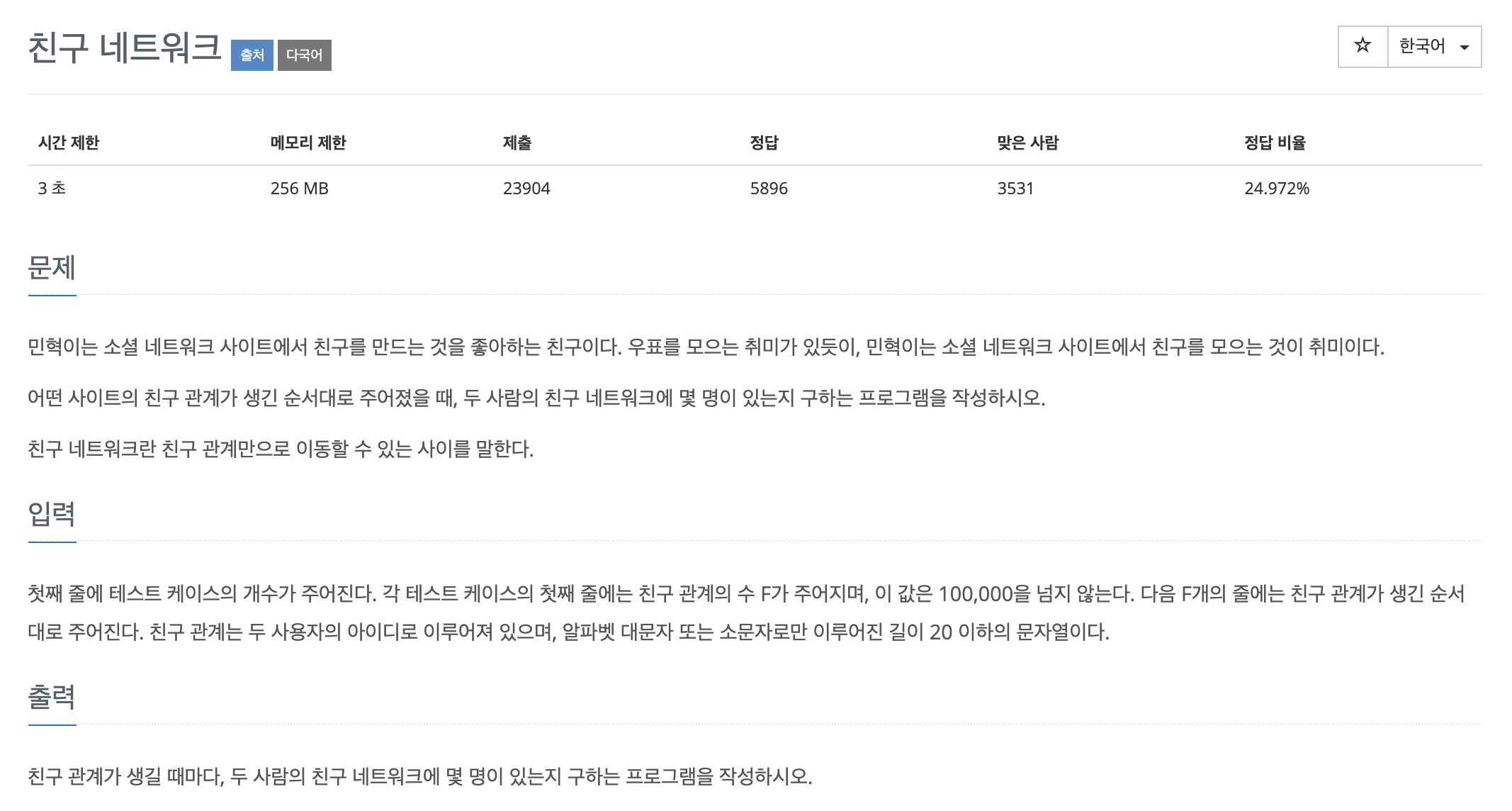
이번 문제는 어떤 사이트의 친구 관계가 생긴 순서대로 주어졌을 때, 두 사람의 친구 네트워크에 몇 명이 있는지 구하는 문제이다. 여기서 친구 네트워크란, 친구 관계만으로 이동할 수 있는 사이를 말한다.

parent를 자기 자신으로 초기화하고, 부모를 찾는 함수 find와 합집합 연산을 해, 같은 부모를 가지도록 하는 union함수를 이용한다.

• Java

import java.io.*;
import java.util.*;

public class Main {
	static int[] parent;
	static int[] cnt;

	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		StringTokenizer st;
		StringBuilder sb = new StringBuilder();

		int T = Integer.parseInt(br.readLine());

		while (T-- > 0) {
			int F = Integer.parseInt(br.readLine());

			parent = new int[F * 2];
			cnt = new int[F * 2];

			for (int i = 0; i < F * 2; i++) {
				parent[i] = i;
				cnt[i] = 1;
			}

			int idx = 0;
			HashMap<String, Integer> map = new HashMap<>();

			for (int i = 0; i < F; i++) {
				st = new StringTokenizer(br.readLine());
				String f1 = st.nextToken();
				String f2 = st.nextToken();

				if (!map.containsKey(f1)) {
					map.put(f1, idx++);
				}

				if (!map.containsKey(f2)) {
					map.put(f2, idx++);
				}
				sb.append(union(map.get(f1), map.get(f2)) + "\n");
			}
		}

		bw.write(sb.toString());
		bw.flush();
		bw.close();
		br.close();
	}

	// x의 부모 찾기
	public static int find(int x) {
		if (x == parent[x])
			return x;

		return parent[x] = find(parent[x]);
	}

	// y 부모를 x 부모로 치환하기 (x > y 일 경우 반대)
	public static int union(int x, int y) {
		x = find(x);
		y = find(y);

		// 항상 x < y인 값이 들어온다고 가정
		if (x != y) {
			parent[y] = x;
			cnt[x] += cnt[y]; // y에 있던 층의 개수를 더해 줌.

			cnt[y] = 1;
		}
		return cnt[x];
	}
}

• Python

import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline

def find(x):
    if x == parent[x]:
        return x
    parent[x] = find(parent[x]) # 부모 테이블 갱신
    return parent[x]

def union(x,y):
    x = find(x)
    y = find(y)

    if x != y:
        parent[y] = x
        number[x] += number[y]
    print(number[x])

test_case = int(input())

for _ in range(test_case):
    parent = {} # dictionary
    number = {}

    f = int(input())

    for _ in range(f):
        f1,f2 = input().split()
        
        if f1 not in parent:
            parent[f1] = f1
            number[f1] = 1
        if f2 not in parent:
            parent[f2] = f2
            number[f2] = 1
        
        union (f1,f2)