Baekjoon Online Judge
algorithm practice
- 단계별 문제풀기
23. 동적 계획법2
조금 더 어려운 동적 계획법 문제를 풀어 봅시다.
Java / Python
7. 앱
발상의 전환이 필요한 냅색 문제
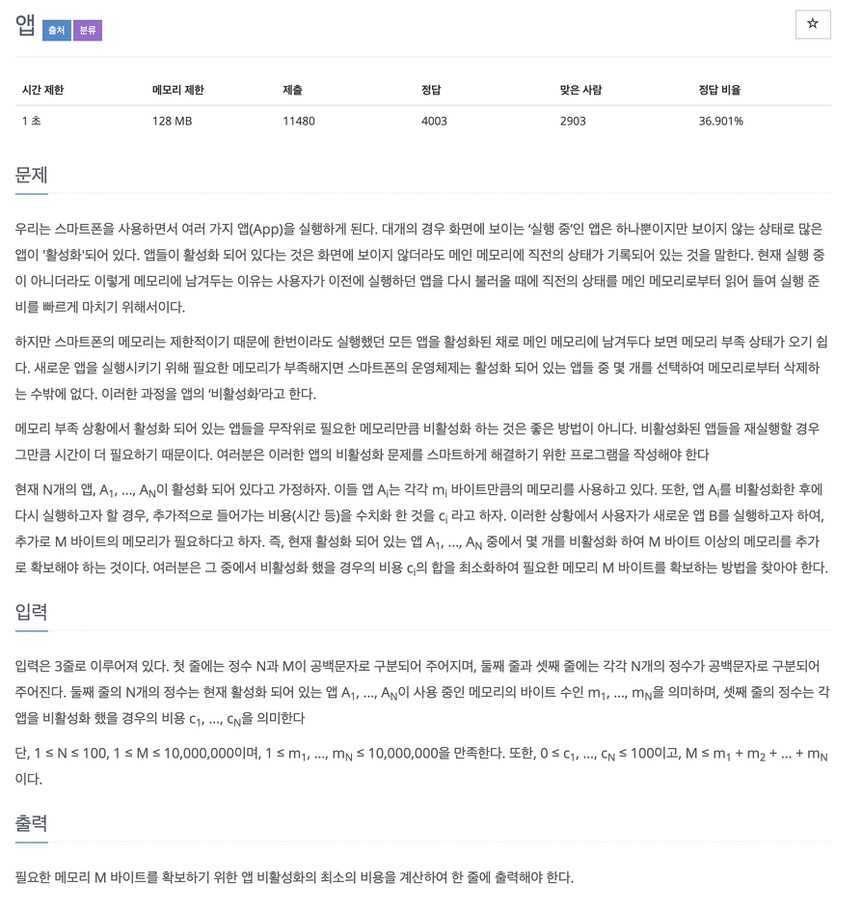
이번 문제는 dp를 이용하는 Knapsack Problem입니다.
담을 수 있는 물건이 나누어 질 수 없는 경우인 0-1 배낭문제의 경우입니다.
각 앱의 메모리들을 memory 배열에 저장하고, 각 앱의 추가 비용들은 cost 배열에 저장하고 dp는 [sum(costs)][N] 크기로 선언합니다. i번째까지 입력된 앱을 사용할 때 cost(j)으로 확보가능한 최대 메모리 크기를 구합니다.
최대 메모리 크기는 dp[i][j] = max(dp[i - 1][j - cost] + memory, dp[i - 1][j]) 와 같은 방식으로 구할 수 있습니다.
(cost : i번째 앱의 비활성화 비용, memory : i번째 앱의 메모리 크기)
- Java
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int result = Integer.MAX_VALUE;
int[] costs = new int[N];
int[] memory = new int[N];
int[][] dp = new int[N][100001];
StringTokenizer st1 = new StringTokenizer(br.readLine());
StringTokenizer st2 = new StringTokenizer(br.readLine());
for(int i = 0; i < N; i++){
memory[i] = Integer.parseInt(st1.nextToken());
costs[i] = Integer.parseInt(st2.nextToken());
}
for(int i = 0; i < N; i++) {
int cost = costs[i];
int mem = memory[i];
for(int j = 0; j <= 10000; j++){
if(i == 0) { // 앱이 하나일 경우 예외처리
if (j >= cost) dp[i][j] = mem;
}else {
if (j >= cost) dp[i][j] = Math.max(dp[i - 1][j - cost] + mem, dp[i - 1][j]);
else dp[i][j] = dp[i - 1][j];
}
if(dp[i][j] >= M) result = Math.min(result, j);
}
}
bw.write(result + "\n");
bw.flush();
bw.close();
br.close();
}
}- Python
import sys
N, M = map(int, sys.stdin.readline().split())
memory = [0] + list(map(int, sys.stdin.readline().split()))
costs = [0] + list(map(int, sys.stdin.readline().split()))
result = sum(costs) + 1
dp = [[0]*(result) for _ in range(N + 1)]
for i in range(1, N + 1):
mem = memory[i]
cost = costs[i]
for j in range(1, len(dp[0])):
if j < cost:
dp[i][j] = dp[i-1][j]
else:
# 같은 cost 내에서 현재 앱을 끈 뒤의 mem와 현재 앱을 끄지 않은 뒤의 mem를 비교
dp[i][j] = max(mem + dp[i-1][j-cost], dp[i-1][j])
if dp[i][j] >= M:
result = min(result, j) #더 작은 cost값으로 갱신
if M != 0:
print(result)
else:
print(0)