Baekjoon Online Judge

algorithm practice

단계별 문제풀기

15. 동적 계획법1

기초적인 동적 계획법 문제들을 풀어봅시다.

Java / Python

14. LCS

9251번

LCS(Longest Common Subsequence)를 구하는 문제

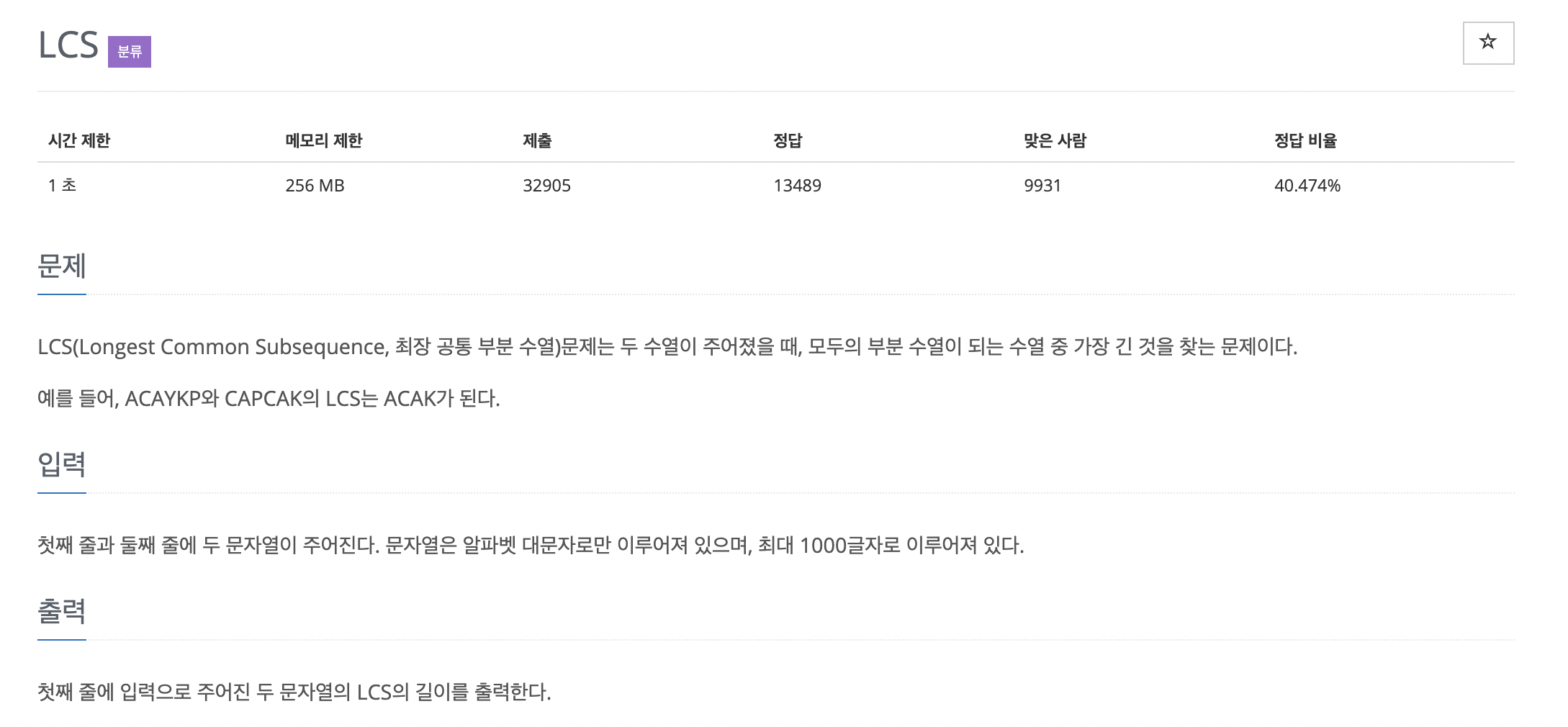
LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제란, 주어진 여러 개의 수열 모두의 부분수열이 되는 수열들 중에 가장 긴 것을 찾는 문제입니다.

문제에서는 예시로, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다고 나와있습니다.

따라서, 코드는 다음과 같은 방식으로 작성했습니다.
S1과 S2에 가장 최근에 추가된 글자가 서로 같을 때
(길이 : (두 글자가 추가되기 전 가장 큰 길이 + 1))
LCS(x,y) = LCS(x-1, y-1) + 1
추가된 글자가 서로 다르다면
(기존에 주어진 문자열로 만들 수 있던 최대 길이)
LCS(x,y) = max(LCS(x-1, y), LCS(x, y-1))

• Java

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;

public class Main{
    
	static Integer[][] dp;
    
	public static char[] string1;
	public static char[] string2;
    
	public static void main(String[] args) throws IOException {
        
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
		string1 = br.readLine().toCharArray();
		string2 = br.readLine().toCharArray();
        
		dp = new Integer[string1.length][string2.length];
		
		System.out.println(LCS(string1.length - 1, string2.length - 1));
        
	}
    
	static int LCS(int x, int y){
    
		if(x == -1 || y == -1) {    // 인덱스 밖일 경우
			return 0;
		}
 
		// 탐색하지 않은 인덱스의 경우
		if(dp[x][y] == null) {
			dp[x][y] = 0;
 
			// str1의 x번째 문자 == str2의 y번째 문자 검사
			if(string1[x] == string2[y]) {
				dp[x][y] = LCS(x - 1, y - 1) + 1;
			}else {
				dp[x][y] = Math.max(LCS(x - 1, y), LCS(x, y - 1));
			}
		}		
		return dp[x][y];
	}
    
}

• Python

import sys 

str1 = sys.stdin.readline().strip().upper()
str2 = sys.stdin.readline().strip().upper()
len1 = len(str1) 
len2 = len(str2) 
dp = [[0] * (len2 + 1) for _ in range(len1 + 1)] 

for i in range(1, len1 + 1): 
    for j in range(1, len2 + 1): 
        if str1[i - 1] == str2[j - 1]: 
            dp[i][j] = dp[i - 1][j - 1] + 1            
        else: 
            dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) 
            
print(dp[-1][-1])