[백준] 17070 파이프 옮기기 1

DP 문제입니다.
문제 총평 : 끝 점을 기준으로 생각해야 하고 예외 처리도 해야 해서 저는 좀 어렵게 느껴졌습니다.

문제풀이 전략
끝점을 기준으로 생각해서 가로, 세로, 대각선으로 올 수 있는 모든 경우의 수를 더하면 됩니다.
답이 계속 0이 나와서 해맸는데 j가 1부터 시작하면 test[0][0][1] = 0으로 덮어씌워지기 때문에 2부터 시작해야 합니다.
방향 정보, 행, 열 까지 총 세가지가 필요하므로 3차원 배열을 선언해줍니다.
예를 들어보겠습니다.
test[0][0][1] = 1 파이프는 가로로 놓여있으며 (0, 1)에 파이프의 끝이 존재합니다.
초기조건은 test[0][0][1] = 1입니다.

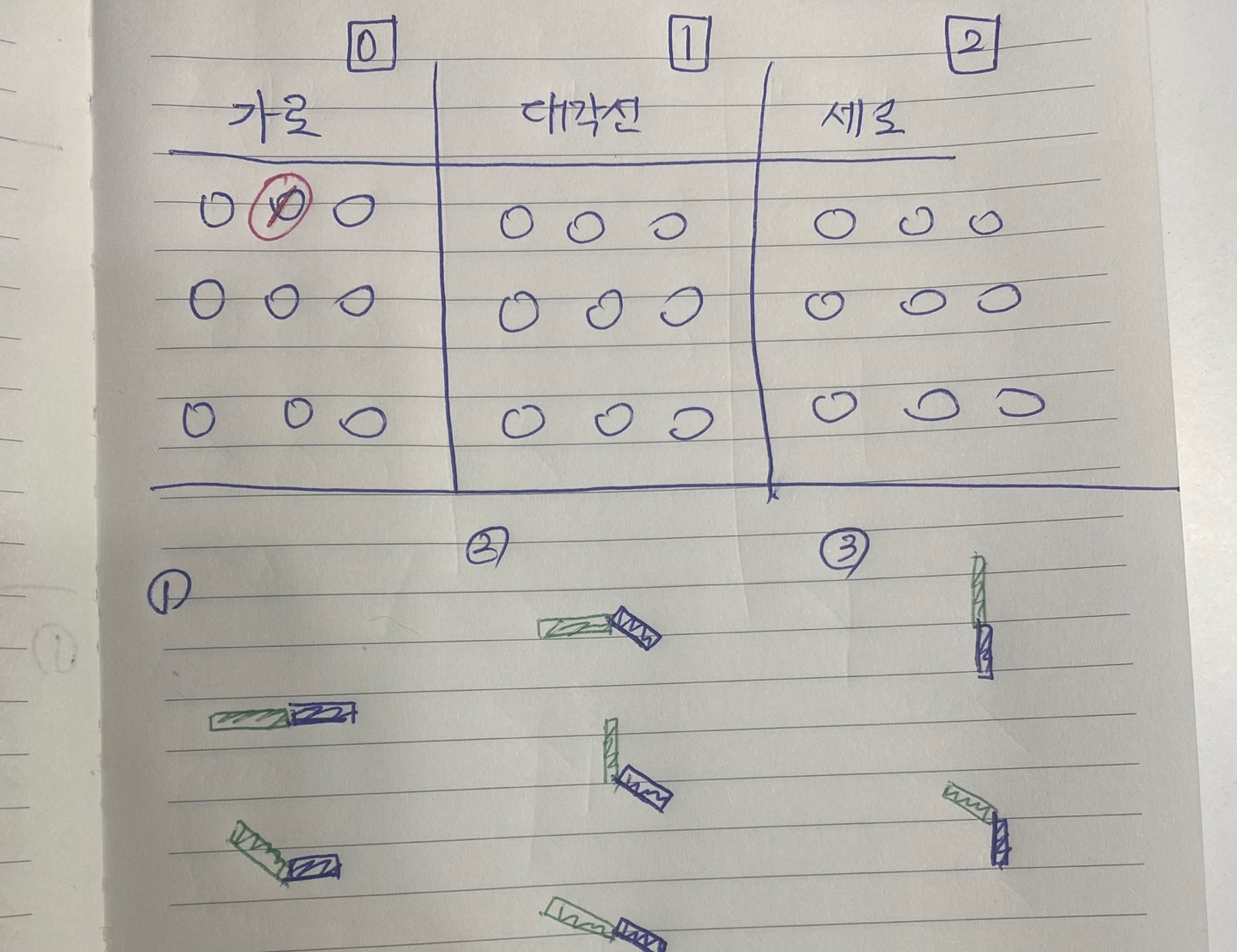
그 밑에 있는 그림은 파이프가 가로, 대각선, 세로 일 때 이전 파이프가 올 수 있는 경우입니다.
그래서 도출해 낼 수 있는 일반항은 다음과 같이 나타낼 수 있습니다.

파이프 가로 : test[0][i][j] = test[1][i][j-1] + test[0][i][j-1]

파이프 세로 : test[2][i][j] = test[2][i-1][j] + test[1][i-1][j]

파이프 대각선: test[1][i][j] = test[0][i-1][j-1]+ test[1][i-1][j-1] + test[2][i-1][j-1]

그리고 이것을 모두 더하면 답이 나옵니다.
하지만, 예외의 경우가 있죠!
1. 벽일 경우 -> pass
2. i가 0일 경우 -> 가로만 가능
3. 대각선일 경우에, 윗쪽과 왼쪽이 모두 비어있어야 합니다. -> ㅇㅇ

n = int(input())
box = [list(map(int, input().split())) for _ in range(n)]
# [0, 1, 2 : 가로, 대각선, 세로], 행, 열
test = [[[0 for _ in range(n)] for j in range(n)] for _ in range(3)]
test[0][0][1] = 1
def dp():
	for i in range(n):
		for j in range(2, n):
			if box[i][j] == 1:
				continue
			test[0][i][j] = test[1][i][j-1] + test[0][i][j-1]
			if i == 0:
				continue
			test[2][i][j] = test[2][i-1][j] + test[1][i-1][j]
			if box[i-1][j] == 1 or box[i][j-1] == 1:
				continue
			test[1][i][j] = test[0][i-1][j-1]+ test[1][i-1][j-1] + test[2][i-1][j-1]
	return test[0][n-1][n-1] + test[1][n-1][n-1] + test[2][n-1][n-1]
print(dp())