Prim's Algorithm과 Kruskal's Algorithm은 Mininum Spanning Tree를 만드는 알고리즘이다.
Minimum Spanning Tree
그래프 G(V,E)가 있다고 하자. (V=vertex의 개수, E= edge의 개수)
또 다른 그래프 G'(V',E')가 G의 spanning tree 일 때, 다음 조건을 만족한다.
(1) V' = V
(2) E'는 E의 부분집합
(3) E' = |V| - 1
spanning tree는 하나만 존재하지 않으며, 복수의 spanning tree가 존재할 수 있다.
뭔 수학 교과서 정리처럼 써놨는데 그냥 정제되지 않은 언어로 말하면 그래프 G의 vertex는 전부 가지고 있으면서 그래프 G의 원래 edge들의 부분집합인 |V|-1개의 edge를 가지는 + 모든 vertex가 연결되어 있는(중간에 끊겨있으면 안된다) tree 라고 보면 된다.
그리고 다수의 spanning tree중에서 각 edge의 weight(cost)의 합이 가장 작은 spanning tree가 minimum spanning tree가 된다.
Prim's Algorithm
다음과 같은 Graph를 예시로 들어보자.
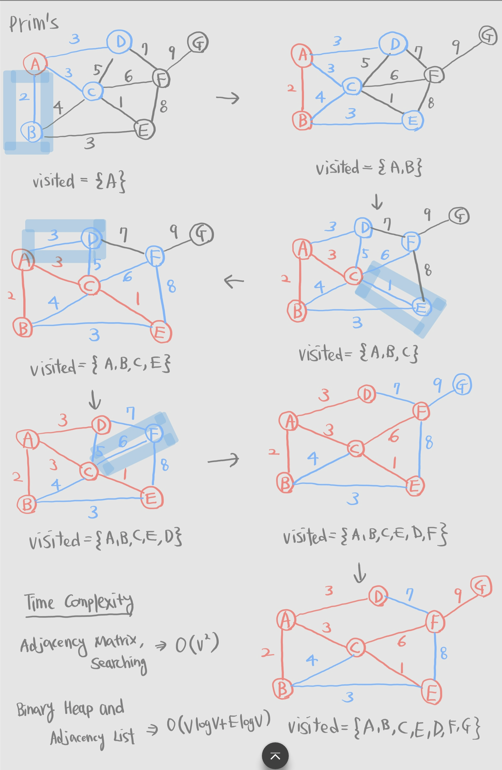
prim's algorithm은 어느 vertex에서 시작해도 상관이 없다. (Kruskal Algorithm과는 다르게.) A에서 시작해보자. A를 일단 visited 집합에 넣는다. 그 다음 A에 인접한 edge들 중에서 cost가 가장 작은 edge를 선택한다. (cost가 가장 작은 edge가 복수이면 아무거나 고르자)
A다음 B를 선택했다고 치자. 현재 visited 집합에는 A와 B가 있다. visited 집합 안에 있는 vertex인 A와 B에 인접한 edge들 중에서
-아직 방문하지 않았고
-cost가 가장 작은 edge
를 또 다시 선택한다. 이 때 주의할 점은 새로 선택할 edge가 cycle을 만들게 되면 안된다. 이 말은 다음으로 선택할 edge 양쪽에 있는 vertex가 이미 visited 집합에 들어가 있으면 안된다는 말과 같다.
위의 그림과 같이 visited 집합 안의 vertex들에 인접한 edge들 중에 cost가 가장 작은 건 B와 E를 잇는 edge인데, 이 edge를 선택하면 cycle이 만들어 지므로 다른 edge를 선택해야 한다. C와 B를 연결하는 edge와 C와 D를 연결하는 edge도 마찬가지이다. 그렇기 때문에 C와 F를 연결하는 edge를 선택해야 한다.
위와 같은 과정을 모든 vertex가 visited 될 때 까지, 즉 연결될 때 까지 반복한다. minimum spanning tree의 total edge weights(각 edge의 weight를 더한것)은 모두 같다.(당연하다. 안 같으면 애초에 weight가 더 큰 하나가 minimum이 아닌걸?)
Kruskal's Algorithm
Kruskal's algorithm은 prim's algorithm과 다르게 가장 cost가 작은 edge에서 부터 시작한다.
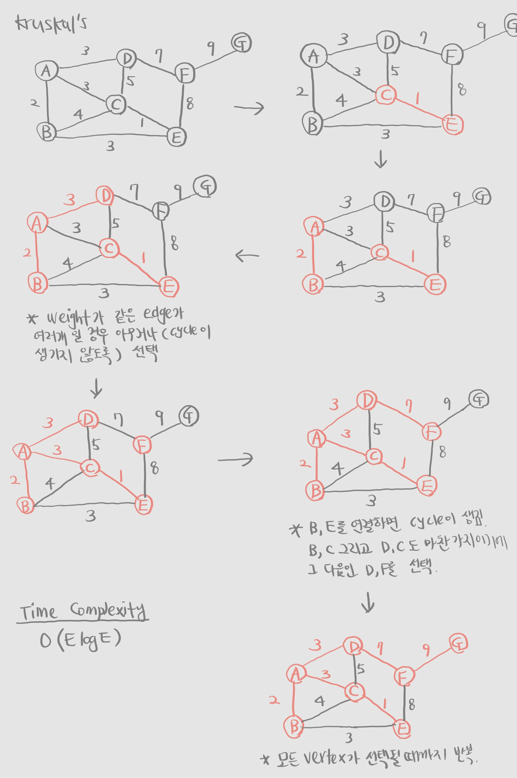
위의 그림에서는 vertex c와 e를 잇는 edge의 cost가 가장 작으므로 해당 edge를 포함시킨다. 그리고 차례차례 cost가 적은 순서대로 + cycle이 만들어지지 않도록 edge를 추가한다. 이것을 모든 vertex가 포함이 될 때 까지 반복한다.