[백준] BOJ_1644 소수의 연속합 JAVA

BOJ_1644 소수의 연속합

문제

하나 이상의 연속된 소수의 합으로 나타낼 수 있는 자연수들이 있다. 몇 가지 자연수의 예를 들어 보면 다음과 같다.

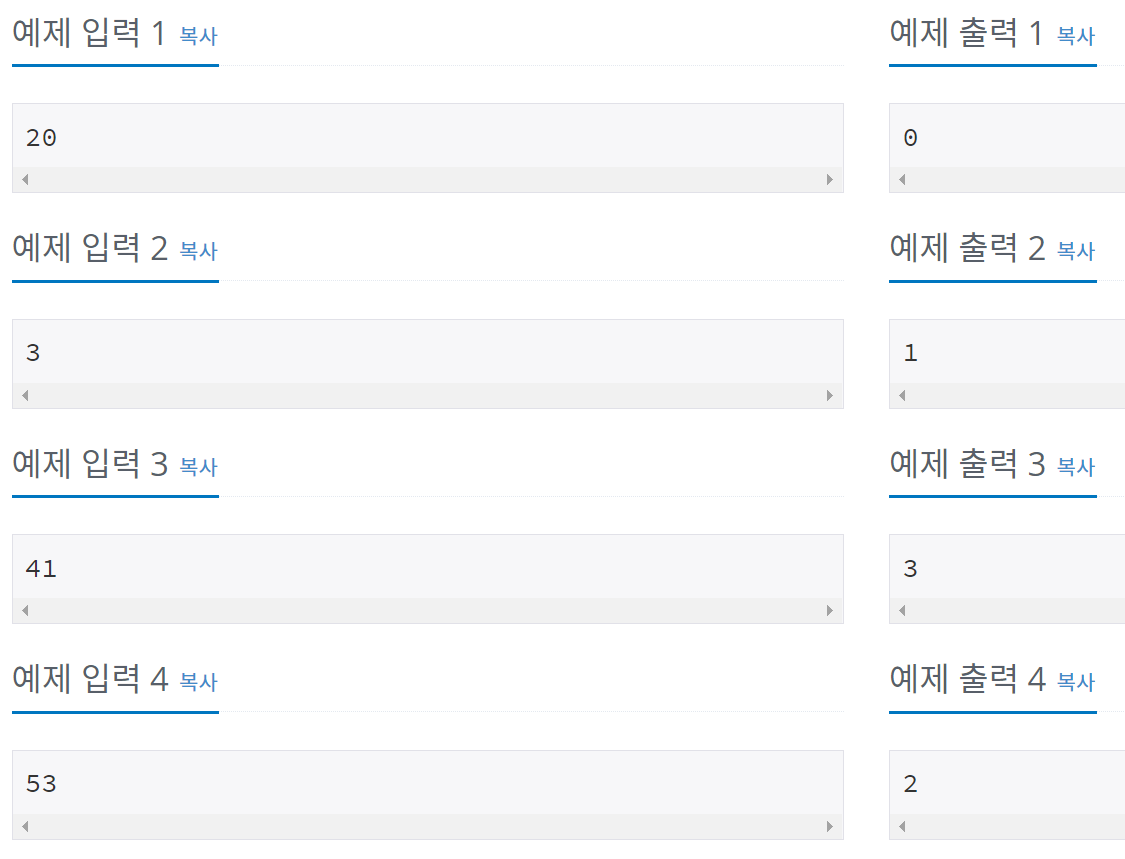
3 : 3 (한 가지)
41 : 2+3+5+7+11+13 = 11+13+17 = 41 (세 가지)
53 : 5+7+11+13+17 = 53 (두 가지)

하지만 연속된 소수의 합으로 나타낼 수 없는 자연수들도 있는데, 20이 그 예이다. 7+13을 계산하면 20이 되기는 하나 7과 13이 연속이 아니기에 적합한 표현이 아니다. 또한 한 소수는 반드시 한 번만 덧셈에 사용될 수 있기 때문에, 3+5+5+7과 같은 표현도 적합하지 않다.

자연수가 주어졌을 때, 이 자연수를 연속된 소수의 합으로 나타낼 수 있는 경우의 수를 구하는 프로그램을 작성하시오.

---

입력

첫째 줄에 자연수 N이 주어진다. (1 ≤ N ≤ 4,000,000)

---

출력

첫째 줄에 자연수 N을 연속된 소수의 합으로 나타낼 수 있는 경우의 수를 출력한다.

---

예제 입&출력

---

소스코드

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class Main {

    private static boolean[] notPrime;
    private static List<Integer> list;

    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);

        int n = sc.nextInt();

        notPrime = new boolean[n + 1];
        notPrime[0] = true;
        notPrime[1] = true;

        //에라토스테네스의 체
        for (int i = 2; i * i <= n; i++) {
            if (!notPrime[i]) {
                for (int j = i * i; j <= n; j += i) {
                    notPrime[j] = true;
                }
            }
        }

        list = new ArrayList<>();
        for (int i = 0; i <= n; i++) {
            if (!notPrime[i]) {
                list.add(i);
            }
        }

        int firstP = 0;
        int secondP = 0;

        int cnt = 0;
        int sum = 0;

        //투 포인터 알고리즘
        while (true) {

            if(sum >= n){
                if(sum == n) cnt++;
                sum -= list.get(firstP++);
            } else if (secondP == list.size()) break;
            else {
                sum += list.get(secondP++);
            }
        }

        System.out.println(cnt);
    }
}

---

Comment

• 앞선 1806_부분합 문제와 유형이 비슷하다.
• 에라토스테네스의 체를 이용하여 소수의 List를 먼저 구했다.

---