
문제 링크
https://www.acmicpc.net/problem/11057
풀이
이것을 정리하면 아래 2가지 Action으로 끝낼 수 있다.
- 2차원 dp를 만들어 1자리수의 경우 1로 초기화한다.
for(int i = 0; i <= 9; i++) {
dp[1][i] = 1;
}- 현재를 k라고 할 때, k의 왼쪽과 k의 왼쪽 대각선 값을 더해서 k에 저장한다.
for(int j = 1; j < 10; j++) {
dp[i][j] = (dp[i][j-1] + dp[i-1][j]) % modular;
sum+= dp[i][j];
}여기에 살을 붙여보자.
- N이라는 자릿수를 입력받아서 2부터 N까지 수행할 것이다.
- 수는 0부터 9까지 사용할 수 있지만, 자릿수에 상관없이 [0]번째는 항상 값이 1이기 때문에 1부터 9까지 수행할 것이다.
그러면 아래와 같은 코드가 된다.
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[][] dp = new int[N+1][10];
for(int i = 0; i <= 9; i++) {
dp[1][i] = 1;
}
for(int i = 2; i <= N; i++) {
int sum = 1;
dp[i][0] = 1; // 0으로 구성되는 경우는 자릿수 상관없이 1이기에
for(int j = 1; j < 10; j++) {
dp[i][j] = (dp[i][j-1] + dp[i-1][j]);
}
}dp를 잘 초기화했다! 이제 오르막 수의 count를 구해야 한다.
알고 있는 조건들
- 1자릿수는 오르막 수의 개수가 10개다. (0~9까지 각각)
int[] count = new int[N+1]; // 0~N까지 접근 가능
count[1] = 10;count[]은 각각 인덱스가 오르막 count를 담고 있다.
그러니 1부터 10까지 연산을 수행한 다음에 그 sum을 더했다가 count[i] 등에 담으면 된다.
또한 우리는 오버플로우를 방지하기 위해 주어진 수로 모듈러 연산을 해줘야 한다.
int modular = 10_007;
for(int i = 2; i <= N; i++) {
int sum = 1;
dp[i][0] = 1; // 0으로 구성되는 경우는 자릿수 상관없이 1이기에
for(int j = 1; j < 10; j++) {
dp[i][j] = (dp[i][j-1] + dp[i-1][j]) % modular;
sum+= dp[i][j];
}
count[i] = sum % modular;
}나의 경우 3중 for문보다 이게 더 이해가 잘 가서 이걸 정리했다.
최종 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[][] dp = new int[N+1][10];
int[] count = new int[N+1];
count[1] = 10;
for(int i = 0; i <= 9; i++) {
dp[1][i] = 1;
}
// Arrays.fill(dp[1], 1);
int modular = 10_007;
for(int i = 2; i <= N; i++) {
int sum = 1;
dp[i][0] = 1; // 0으로 구성되는 경우는 자릿수 상관없이 1이기에
for(int j = 1; j < 10; j++) {
dp[i][j] = (dp[i][j-1] + dp[i-1][j]) % modular;
sum+= dp[i][j];
}
count[i] = sum % modular;
}
System.out.println(count[N]);
}
}헤맴기
일단 문제에서 1자리일 때와 2자리일 때의 모든 경우의 수를 적어보았다.
* 1자리(1): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
* 2자리(1): 00, 01, 02, 03, 04, 05, 06, 07, 08, 09
* 2자리(2): 10(k<j), 11(k=j), 12(k>j && k<10), 13(k>j && k<10), 14(k>j && k<10), 15(k>j && k<10), 16(...), 17, 18, 19
* 2자리(3): 22, 23, 24, 25, 26, 27, 28, 29
* 2자리(4): 33, 34, 35, 36, 37, 38, 39
* 2자리(5): 44, 45, 46, 47, 48, 49
* 2자리(6): 55, 56, 57, 58, 59
* 2자리(7): 66, 67, 68, 69
* 2자리(8): 77, 78, 79
* 2자리(9): 88, 89
* 2자리(10): 99
이 문제는 3중 for문과 2차원 dp 배열을 사용해야 하는데
2자리(22)에서 k의 범위를 적어보았다.
k의 범위는 앞자리 숫자보다 같거나 크면서 9보다 작거나 같을 때까지다.
보다시피 j의 숫자가 커질 수록 k의 갯수가 줄어든다.
(여기서 j는 십의 자리, k는 일의 자리다.)
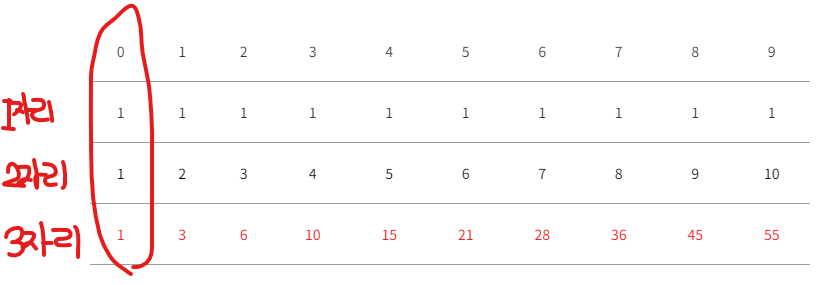
표를 좀 빌리자면,

이 문제는 길이가 3인 경우로만 넘어가도 숫자가 커져서 나처럼 일일이 모든 케이스를 치는 것은 어려웠다.
근데 규칙을 알고보니 1자리, 2자리인 경우만 제대로 정리해도 아래와 같이 보이기 시작했다.
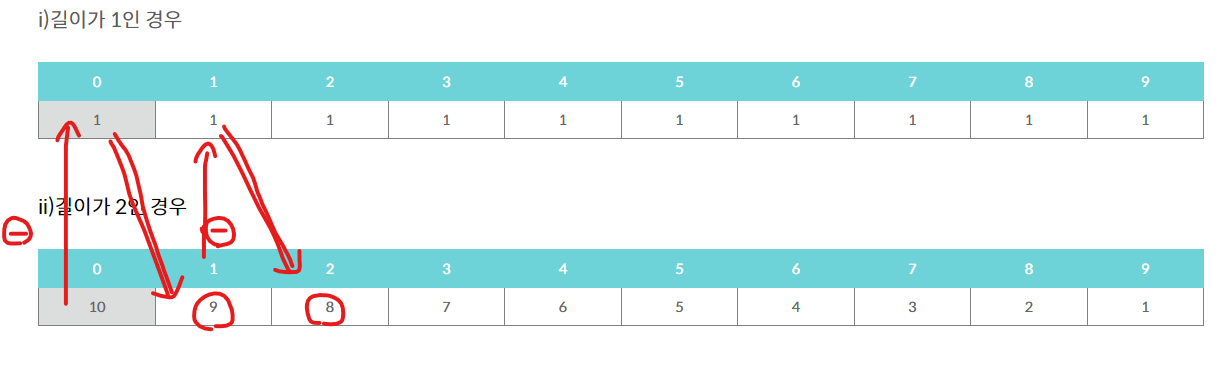
근데? 2자리의 경우 저 0번째 index 자리의 10을 어디서 설정하는 것인지 모르겠다. 그래서 위의 설명한 코드로 돌아가게 된다.
(인덱스가 0일때 무조건 값이 1이니까 이유 설명됨)
표의 출처
https://jackine.tistory.com/7
