[백준, 자바] 1149번 - RGB

문제 링크
https://www.acmicpc.net/problem/1149

최종 코드(정답)

import java.io.*;

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine()); // 칠할 집의 개수

        int[][] dp = new int [n+1][n+1]; // 각 집을 칠하는 비용을 저장할 배열

        for (int i = 1; i <= n; i++) {
            String[] input = br.readLine().split(" ");
            int red = Integer.parseInt(input[0]);
            int green = Integer.parseInt(input[1]);
            int blue = Integer.parseInt(input[2]);

            dp[i][1] = Math.min(dp[i-1][2], dp[i-1][3]) + red;
            dp[i][2] = Math.min(dp[i-1][1], dp[i-1][3]) + green;
            dp[i][3] = Math.min(dp[i-1][1], dp[i-1][2]) + blue;
        }
        int min = Math.min(dp[n][1], Math.min(dp[n][2], dp[n][3]));
        System.out.println(min);
    }
}

풀이

• 빨간집은 이전 집이 초록색이거나 파란색일 때 가능하다.
• 초록집은 이전 집이 빨간색이거나 파란색일 때 가능하다.
• 파란집은 이전 집이 빨간색이거나 초록색일 때 가능하다.

그림으로 나타내면 아래처럼 된다.

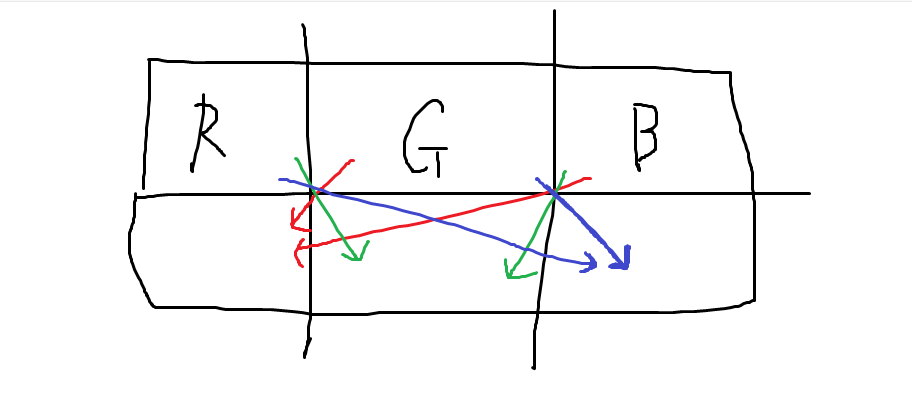
파란색 화살표는 빨간색과 녹색집만이 i번째에 파란집을 고를 수 있다는 뜻이다.

맨 마지막줄 i에서 [0], [1], [2] 중에서 원하는 걸 고르면 될 것 같다.

틀린 코드

import java.io.*;

public class Main {

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine()); // 칠할 집의 개수

        int[] dp = new int [n + 1]; // 각 집을 칠하는 비용을 저장할 배열
        int[] colors = new int [n + 1]; // 0부터 6까지

        for (int i = 1; i <= n; i++) {
            String[] input = br.readLine().split(" ");
            int red = Integer.parseInt(input[0]);
            int green = Integer.parseInt(input[1]);
            int blue = Integer.parseInt(input[2]);

            if (dp[i-1] == 0) {
                dp[i] = Math.min(red, Math.min(green, blue));
                colors[i] = red < green ? (red < blue ? 1 : 3) : (green < blue ? 2 : 3);
            } else {
                int prevColorIdx = colors[i-1];
                System.out.println("prevColorIdx = " + prevColorIdx);
                switch (prevColorIdx) {
                    case 1:
                        dp[i] = dp[i-1] + Math.min(green, blue);
                        colors[i] = green < blue ? 2 : 3;
                        break;
                    case 2:
                        dp[i] = dp[i-1] + Math.min(red, blue);
                        colors[i] = red < blue ? 1 : 3;
                        break;
                    case 3:
                        dp[i] = dp[i-1] + Math.min(red, green);
                        colors[i] = red < green ? 1 : 2;
                        break;
                }
            }
        }
        System.out.println(dp[n]);
    }
}

후기
마치 저번 이동하기 문제와 같다.
현 위치에서 생각하지 말고, 현재 이전 위치가 어디인지, 어디서부터 여기까지 오는지 referrer를 생각해야 한다.

집별값이 각각으로는 최솟값이 좋아보일지라도 다 합해봤을 때는 모르는 일이다. 그래서 모든 경우의 수를 구해야 하고, 성능상 동적 프로그래밍을 사용하는 것이다.

큰 그림을 봐야 한다는 교훈...