
문제 링크
https://www.acmicpc.net/problem/15990
1,2,3 더하기 시리즈 중 하나인데, 같은 숫자가 2번 이상 연속되면 안된다는 조건이 문제를 더 어렵게 만들었다.
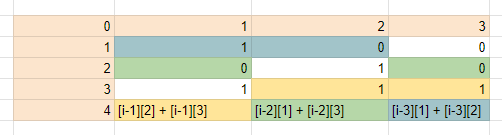
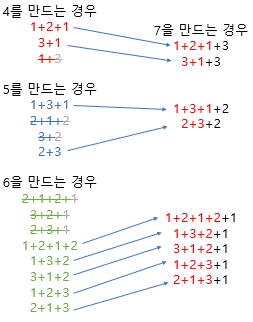
개인적으로 더하는 여기 부분을 이해 못했었다.
마지막이 1로 끝나는 경우, 마지막이 2로 끝나는 경우, 마지막이 3으로 끝나는 경우를 각각 고려한 계산을 해야 한다.
참고
https://velog.io/@jkh9615/알고리즘-백준-15990-1-2-3-더하기-5-Java
답안들을 보면 각각 % modular를 하고도 마지막에 sb에 더할 때도 또 % modular를 한다.
한번만 하면 안되는 건가? 라는 생각이 들어서 검색해봤더니 다름 아닌 오버플로우 방지용이라고 한다.
마지막에 % modular 연산을 제외하는 것은 가능하지만, 이는 오버플로우를 방지할 수 없습니다. 동적 프로그래밍에서는 작은 문제의 해를 이용하여 큰 문제의 해를 구합니다. 이 과정에서 작은 문제의 해가 이미 오버플로우가 발생한 상태라면, 그 오류는 큰 문제의 해를 구하는 과정에도 영향을 미칩니다. 따라서, 각 단계에서 % modular 연산을 수행하여 오버플로우를 방지해야 합니다. 또한, 이 문제에서는 결과값을 1,000,000,009로 나눈 나머지를 출력하라고 명시되어 있습니다. 따라서, 계산 과정에서 모든 결과값에 대해 모듈러 연산을 수행해야 합니다. 마지막으로, 모듈러 연산은 덧셈, 뺄셈, 곱셈에 대해 분배 법칙이 성립합니다. 즉, (a + b) % p는 (a % p + b % p) % p와 같습니다. 따라서, 계산 과정에서 각 단계마다 모듈러 연산을 수행하면 최종 결과값이 올바르게 계산됩니다.
최종 코드
import java.io.BufferedReader;
import java.io.IOException;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new java.io.InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int n = Integer.parseInt(br.readLine());
int maxOfN = 100_000;
// dp를 선언한다. (2차원, 3까지 가로로 저장가능한)
long[][] dp = new long[maxOfN+ 1][4];
// 10000009로 나눈 나머지를 구해야 하므로 공통 변수로 뺀다.
int modular = 1000_000_009;
// 1,2,3의 경우를 for 반복 전에 초기화한다.
dp[1][1] = 1;
dp[2][2] = 1;
dp[3][1] = dp[3][2] = dp[3][3] = 1;
// 4부터 n까지 dp에 값을 저장한다.
// +1로 끝나는 경우, +2로 끝나는 경우, +3으로 끝나는 경우를 고려해야 한다.
// 일단 문제의 최대 max까지 for문을 돌려서 dp를 초기화한다.
for(int i = 4; i <= maxOfN; i++) {
dp[i][1]= (dp[i-1][2] + dp[i-1][3]) % modular;
dp[i][2]= (dp[i-2][1] + dp[i-2][3]) % modular;
dp[i][3]= (dp[i-3][1] + dp[i-3][2]) % modular;
}
// 그 다음에 for문으로 입력값 [t][1] [t][2] [t][3]을 더해서 sb에 추가한다.
for(int i = 0; i < n; i++) {
int t = Integer.parseInt(br.readLine());
sb.append((dp[t][1] + dp[t][2] + dp[t][3]) % modular).append("\n");
}
System.out.println(sb);
}
}주의사항
- [i-3][3]을 위해서는 사전에 dp[][]를 dp[3][]까지 초기화를 해놓는다.
- 오버플로우를 막기 위해서 연산별로
% modular를 한다.
