[백준, 자바] 1929번 - 소수 구하기

위 문제는 백준 기초 > 소수 찾기와 관련이 있다.
https://www.acmicpc.net/problem/1978

소수 구하기

import java.io.*;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();

        StringTokenizer st = new StringTokenizer(br.readLine());
        int start = Integer.parseInt(st.nextToken());
        int end = Integer.parseInt(st.nextToken());

        boolean[] isPrime = new boolean[end + 1];
        for (int i = 0; i < isPrime.length; i++) {
            isPrime[i] = true;
        }

        isPrime[0] = isPrime[1] = false;
        for (int i = 2; i * i <= end; i++) {
            if (isPrime[i]) {
                for (int j = i * i; j <= end; j += i) {
                    isPrime[j] = false;
                }
            }
        }
        
        for(int i = start; i <= end; i++) {
            if(isPrime[i]) sb.append(i).append("\n");
        }

        System.out.println(sb);
    }

}

풀이

Q. 에라토스테네스의 체

소수 판별 알고리즘으로 유명하다.
특정한 숫자의 제곱근 까지만 약수의 여부를 검증하면 O(N^1/2) 시간 복잡도로 빠르게 판별할 수 있다고 한다.

특징

• 2부터 특정 수의 배수를 지우되, 자기 자신과 이미 지운 수는 건너뛴다.
• 배열로 소수인지 아닌지 판별값을 넣어 놓고 분기처리해서 출력한다.

설명 아래 링크 참고

https://loosie.tistory.com/267

for문 i와 j를 풀어내보면 아래와 같다. (백준 예제를 기준으로 3과 16사이 범위를 기준으로 하였다.)

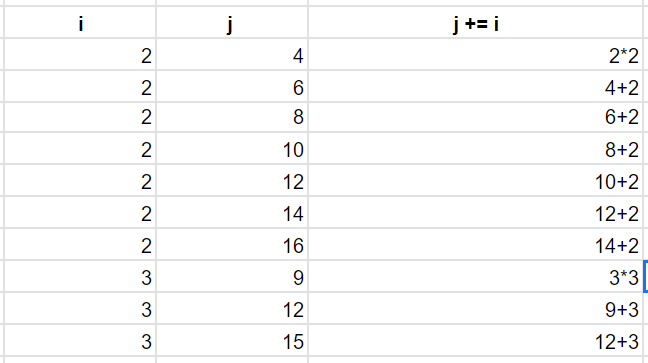
결과적으로 j에 해당하는 숫자들은 소수가 아니다.
처음에는 i*i를 한 다음에 계속 j = j + i를 계속한다.

미리 값의 범위만큼 boolean[]을 만들어 놓고 소수가 아닌 인덱스 주소에 false 처리를 한다.
(물론 LinkedList 등으로도 처리할 수 있다)

후기

for문 조건도 제대로 풀어낼 수 있도록 연습이 필요해 보인다.