문자열 Prefix와 Suffix 일치 문제

문제 설명

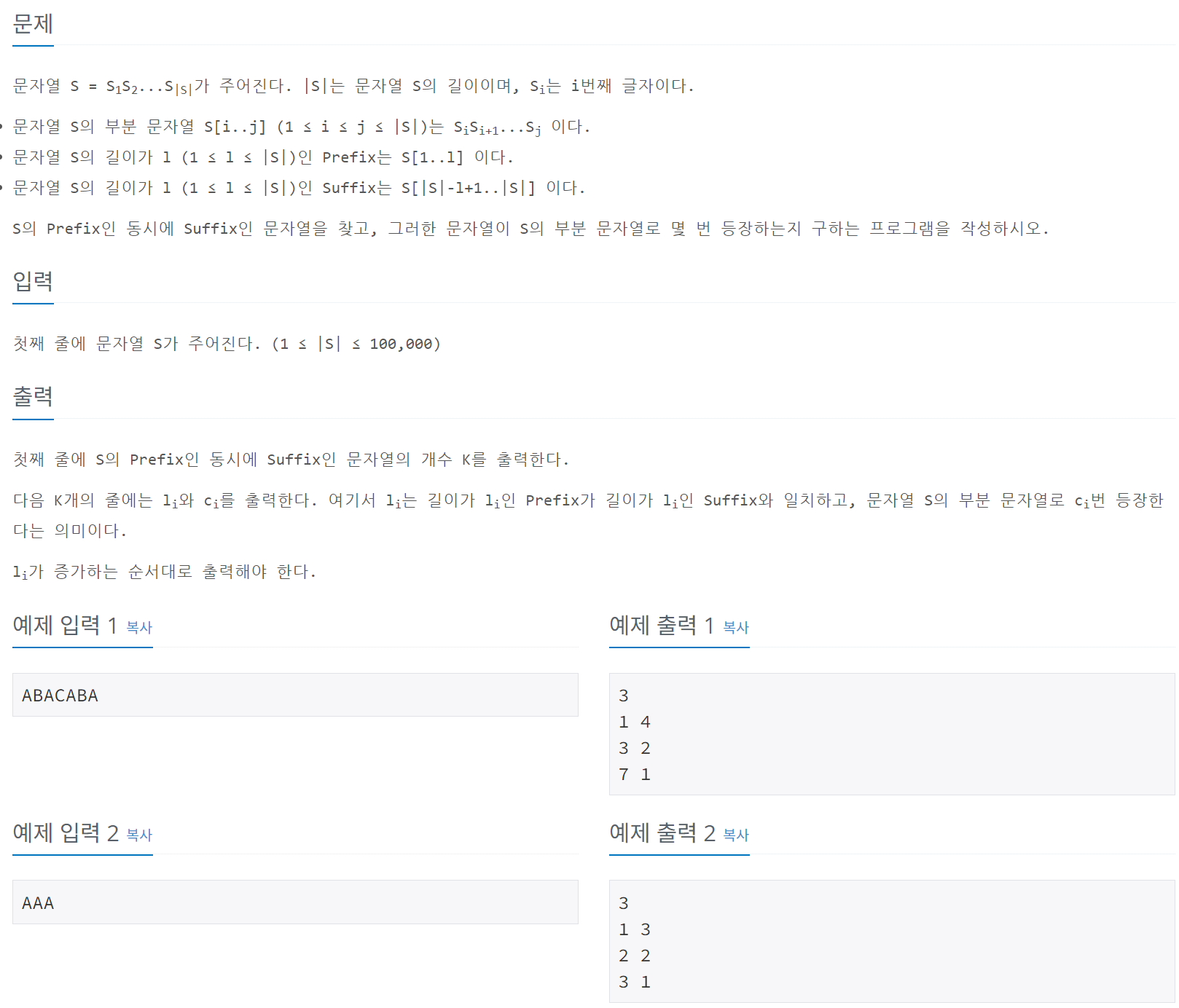
문자열 ( S )가 주어졌을 때:

1. ( S )의 Prefix이면서 동시에 Suffix인 문자열을 구해야 한다.
2. 구한 문자열이 ( S )의 부분 문자열로 몇 번 등장하는지 계산해야 한다.
3. 결과를 Prefix 길이가 작은 순서로 정렬하여 출력해야 한다.

입력

• 문자열 ( S ): 길이 최대 100,000

출력

• Prefix와 Suffix가 일치하는 문자열의 개수 ( K )
• 각 ( K )에 대해 ( l_i ) (길이)와 ( c_i ) (등장 횟수)

코드

import java.util.*;

public class Main {
    static String s;
    static int[] suffixArray, rank, lcp, pi;
    static int n;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        s = sc.next();
        n = s.length();

        buildSuffixArray();
        buildLCPArray();
        buildPiArray();

        int[] dp = new int[n];
        Arrays.fill(dp, -1);
        List<int[]> results = new ArrayList<>();

        results.add(new int[]{n, 1});
        int x = pi[n - 1];
        while (x > 0) {
            int index = rank[n - x];
            results.add(new int[]{x, calculateCount(index, dp)});
            x = pi[x - 1];
        }

        System.out.println(results.size());
        for (int i = results.size() - 1; i >= 0; i--) {
            System.out.println(results.get(i)[0] + " " + results.get(i)[1]);
        }
    }

    static void buildSuffixArray() {
        suffixArray = new int[n];
        rank = new int[n];
        int[] tempRank = new int[n];
        Integer[] order = new Integer[n];
        for (int i = 0; i < n; i++) {
            suffixArray[i] = i;
            rank[i] = s.charAt(i) - 'A';
            order[i] = i;
        }

        for (int length = 1; length < n; length *= 2) {
            int finalLength = length;
            Arrays.sort(order, (a, b) -> {
                if (rank[a] != rank[b]) return Integer.compare(rank[a], rank[b]);
                int rankA = (a + finalLength < n) ? rank[a + finalLength] : -1;
                int rankB = (b + finalLength < n) ? rank[b + finalLength] : -1;
                return Integer.compare(rankA, rankB);
            });

            for (int i = 0; i < n; i++) {
                suffixArray[i] = order[i];
            }

            tempRank[suffixArray[0]] = 0;
            for (int i = 1; i < n; i++) {
                boolean sameRank = rank[suffixArray[i]] == rank[suffixArray[i - 1]]
                        && ((suffixArray[i] + length < n ? rank[suffixArray[i] + length] : -1)
                        == (suffixArray[i - 1] + length < n ? rank[suffixArray[i - 1] + length] : -1));
                tempRank[suffixArray[i]] = tempRank[suffixArray[i - 1]] + (sameRank ? 0 : 1);
            }
            System.arraycopy(tempRank, 0, rank, 0, n);
        }
    }

    static void buildLCPArray() {
        lcp = new int[n];
        int h = 0;
        for (int i = 0; i < n; i++) {
            if (rank[i] > 0) {
                int j = suffixArray[rank[i] - 1];
                while (i + h < n && j + h < n && s.charAt(i + h) == s.charAt(j + h)) {
                    h++;
                }
                lcp[rank[i]] = h;
                if (h > 0) h--;
            }
        }
    }

    static void buildPiArray() {
        pi = new int[n];
        int j = 0;
        for (int i = 1; i < n; i++) {
            while (j > 0 && s.charAt(i) != s.charAt(j)) {
                j = pi[j - 1];
            }
            if (s.charAt(i) == s.charAt(j)) {
                j++;
            }
            pi[i] = j;
        }
    }

    static int calculateCount(int x, int[] dp) {
        if (dp[x] != -1) return dp[x];
        dp[x] = 1;
        for (int i = x + 1; i < n; i++) {
            if (lcp[i] >= n - suffixArray[x]) {
                dp[x] += calculateCount(i, dp);
                i += calculateCount(i, dp) - 1;
            } else {
                break;
            }
        }
        return dp[x];
    }
}

코드 설명

1. Suffix Array 구성

   • Suffix Array는 문자열의 모든 Suffix를 사전순으로 정렬한 뒤, 해당 위치의 인덱스를 저장한 배열이다.
   • 이 배열을 구성하기 위해 (O(N \log^2 N)) 복잡도의 방법을 사용한다.

2. LCP Array 생성

   • LCP Array는 정렬된 Suffix Array 상의 인접한 Suffix 간 공통 접두사 길이를 저장한다.
   • 이를 통해 Suffix들 간 유사도를 빠르게 계산할 수 있다.

3. KMP의 Prefix Function 생성

   • (pi[i]): 문자열의 (S[1..i])의 Prefix 중 Suffix도 되는 최대 길이를 저장한다.
   • 이 배열을 사용해 Prefix-Suffix 관계를 탐색한다.

4. 등장 횟수 계산

   • DP 배열: (dp[x])는 Suffix Array 상의 (x) 위치에 해당하는 Suffix가 등장하는 횟수를 저장한다.
   • LCP 값을 사용해 동일한 Suffix가 반복되는 구간을 누적해 계산한다.

So...

이 코드는 문자열의 Prefix와 Suffix를 효율적으로 탐색하며, 여러 자료구조(Suffix Array, LCP Array, KMP)를 조합해 문제를 해결한다. 이를 통해 시간 복잡도를 𝑂(𝑁log𝑁)수준으로 유지하며 대규모 입력에도 대응할 수 있다.
구현 과정에서 Suffix Array 정렬과 등장 횟수 계산 로직의 디테일을 이해하는 데 고민이 많았으나, 이를 통해 문자열 처리의 고급 알고리즘을 깊이 이해할 수 있었다.