탈옥 위험도를 최소화하는 감시 배치 문제

문제 설명

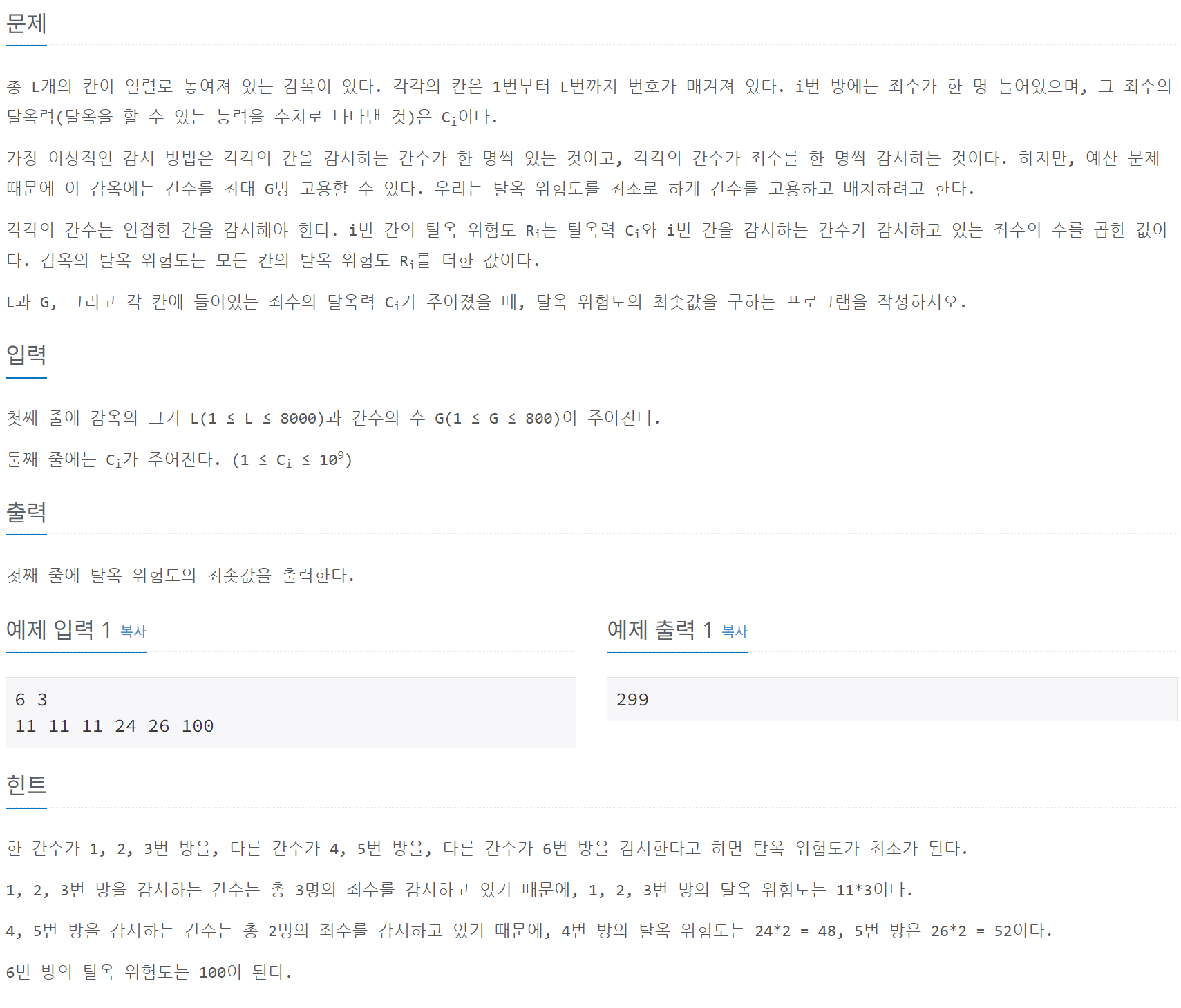
감옥의 ( L )개의 칸에 각각 죄수가 들어있다. 이때, 간수를 최대 ( G )명 고용하여 감옥을 감시할 수 있다. 각 간수는 인접한 칸을 감시해야 하며, 각 칸의 탈옥 위험도는 그 칸의 탈옥력 ( C_i )와 해당 칸을 감시하는 간수가 감시하는 죄수의 수를 곱한 값이다. 감옥 전체의 탈옥 위험도는 모든 칸의 탈옥 위험도를 합한 값이다.

목표는 ( G )명의 간수를 배치하여 감옥의 탈옥 위험도를 최소화하는 것이다.

핵심 아이디어

1. 동적 계획법(DP):

   • ( dp[g][j] ): ( g )명의 간수를 사용하여 1번부터 ( j )번 칸까지 감시했을 때의 최소 탈옥 위험도.
   • ( dp[1][j] )는 ( 1 )명의 간수가 모든 칸을 감시했을 때의 탈옥 위험도와 같다.

2. 비용 함수:

   • ( cost(i, j) ): ( i )번 칸부터 ( j )번 칸까지 한 간수가 감시할 때의 탈옥 위험도.
   • ( cost(i, j) = (pre[j] - pre[i]) \times (j - i) ), 여기서 ( pre[j] )는 누적 합.

3. 분할 정복 최적화:

   • DP 계산에서 최적화를 위해 분할 정복 기법을 활용하여 ( g )번째 간수에서의 최적 분할 지점을 효율적으로 찾는다.

코드

import java.util.*;

public class Main {
    private static final long INF = Long.MAX_VALUE;
    private static long[] arr, pre;
    private static long[][] dp;

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int L = sc.nextInt(); // 감옥 크기
        int G = sc.nextInt(); // 간수 수

        arr = new long[L + 1];
        pre = new long[L + 1];
        dp = new long[G + 1][L + 1];

        // 죄수의 탈옥력 입력 및 누적합 계산
        for (int i = 1; i <= L; i++) {
            arr[i] = sc.nextLong();
            pre[i] = pre[i - 1] + arr[i];
        }

        // 간수 1명일 때의 초기 DP 값
        for (int i = 1; i <= L; i++) {
            dp[1][i] = pre[i] * i;
        }

        // DP 계산 (Divide and Conquer Optimization 사용)
        for (int g = 2; g <= G; g++) {
            computeDP(g, 1, L, 0, L - 1);
        }

        // 결과 출력
        System.out.println(dp[G][L]);
    }

    // 범위 [i, j]의 비용 계산 함수
    private static long cost(int i, int j) {
        return (pre[j] - pre[i]) * (j - i);
    }

    // DP를 분할 정복 최적화 방식으로 계산
    private static void computeDP(int g, int left, int right, int optL, int optR) {
        if (left > right) return;

        int mid = (left + right) / 2; // 중앙 인덱스
        dp[g][mid] = INF; // 초기값 설정
        int bestK = -1;

        // 최적 분할점 탐색
        for (int k = optL; k <= Math.min(optR, mid - 1); k++) {
            long currentCost = dp[g - 1][k] + cost(k, mid);
            if (dp[g][mid] > currentCost) {
                dp[g][mid] = currentCost;
                bestK = k;
            }
        }

        // 왼쪽, 오른쪽 서브 구간 재귀적으로 계산
        computeDP(g, left, mid - 1, optL, bestK);
        computeDP(g, mid + 1, right, bestK, optR);
    }
}

코드 설명

1. 누적합 계산:

   • (pre[i]): 1번 칸부터 (i)번 칸까지의 탑승력 합.
   • 비용 계산을 (O(1))로 하기 위해 누적합을 사용.

2. DP 배열 정의:

   • (dp[g][j]): (g)명의 간수를 사용하여 1번부터 (j)번 칸까지 감시했을 때의 최소 탑승 위험도.

3. 비용 계산:

   • (cost(i, j) = (pre[j] - pre[i]) \times (j - i)).

4. 분할 정복 최적화:

   • (dp[g][j])를 계산할 때 최적 분할 지점을 효율적으로 탐색.
   • 탐색 범위를 줄이기 위해 분할 정복 방식을 사용.

So...

이 문제는 DP와 분할 정복 최적화를 결합하여 대규모 데이터에서도 효율적으로 해결할 수 있다. DP 배열의 크기를 줄이고, 최적화를 통해 복잡도를 크게 감소시켰다. 구현 과정에서 최적화를 위해 비용 계산과 메모리 사용을 신중히 관리한 점이 핵심이다.