수열의 쿼리 처리 문제

문제 설명

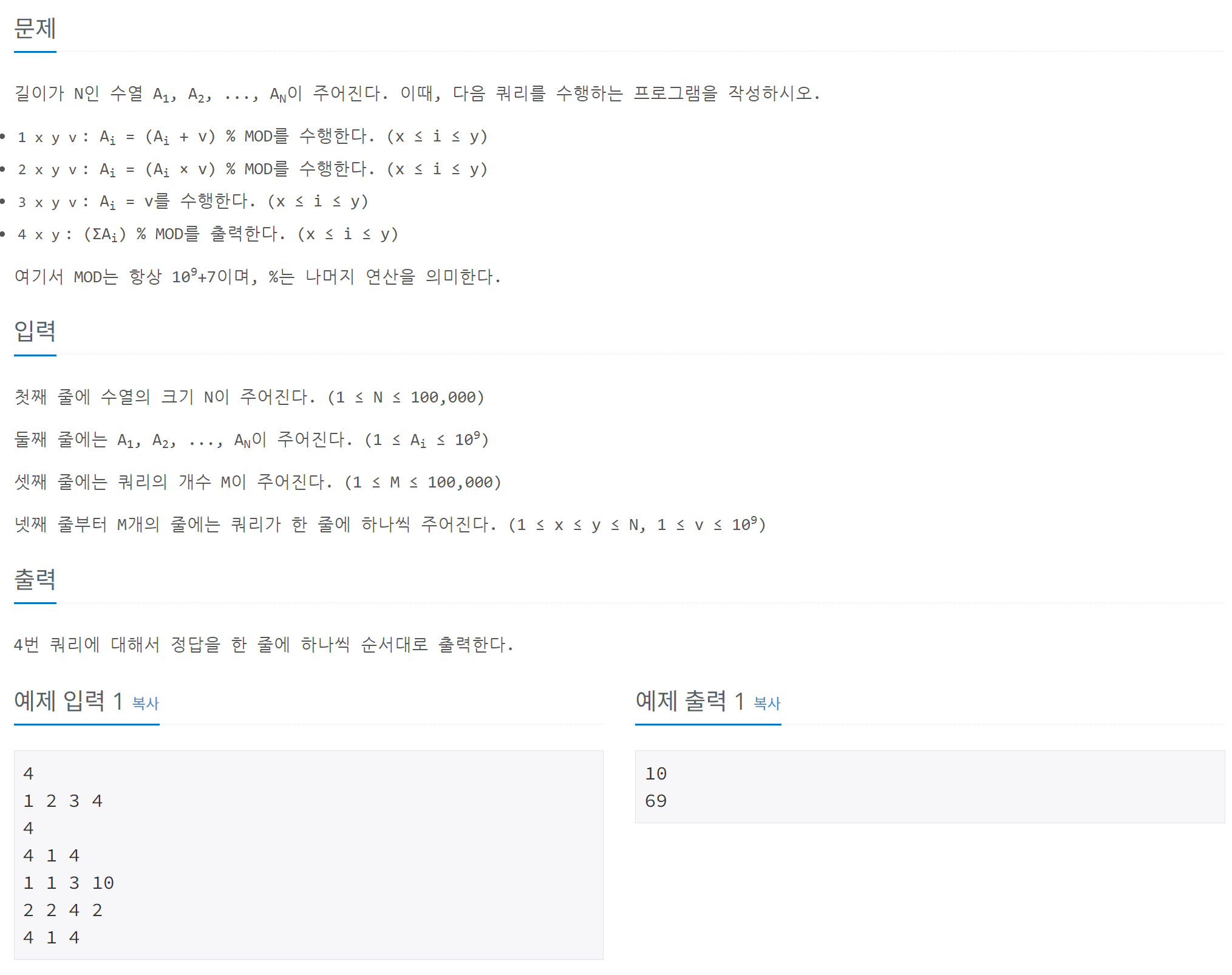
길이가 ( N )인 수열 ( A )에 대해 다양한 연산을 효율적으로 수행해야 한다. 연산은 다음 네 가지이다:
1. 구간 더하기: ( A[x] )부터 ( A[y] )까지 ( v )를 더한 후 MOD로 나눈 나머지를 저장한다.
2. 구간 곱하기: ( A[x] )부터 ( A[y] )까지 ( v )를 곱한 후 MOD로 나눈 나머지를 저장한다.
3. 구간 대체: ( A[x] )부터 ( A[y] )까지 모든 값을 ( v )로 대체한다.
4. 구간 합 출력: ( A[x] )부터 ( A[y] )까지의 합을 MOD로 나눈 나머지를 출력한다.

핵심 아이디어

1. 세그먼트 트리:

   • 구간에 대한 연산(합, 곱, 대체)을 효율적으로 수행하기 위해 세그먼트 트리를 사용한다.

2. 지연 전파 (Lazy Propagation):

   • 구간 연산에서 모든 노드를 즉시 갱신하지 않고, 필요한 시점에만 갱신하는 방식이다.
   • 이를 통해 구간에 대한 대체, 곱하기, 더하기 연산을 효율적으로 처리한다.

3. MOD 연산:

   • 모든 연산 결과는 MOD를 적용하여 계산한다.

코드

import java.io.*;
import java.util.*;

public class Main {
    static final int MOD = 1000000007;
    static int N, M;
    static long[] arr, tree, mulLazy, addLazy;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
        StringTokenizer st;

        N = Integer.parseInt(br.readLine());
        arr = new long[N];
        tree = new long[4 * N];
        mulLazy = new long[4 * N];
        addLazy = new long[4 * N];
        Arrays.fill(mulLazy, 1);

        st = new StringTokenizer(br.readLine());
        for (int i = 0; i < N; i++) {
            arr[i] = Long.parseLong(st.nextToken());
        }

        init(1, 0, N - 1);

        M = Integer.parseInt(br.readLine());
        for (int i = 0; i < M; i++) {
            st = new StringTokenizer(br.readLine());
            int order = Integer.parseInt(st.nextToken());
            int x = Integer.parseInt(st.nextToken()) - 1;
            int y = Integer.parseInt(st.nextToken()) - 1;

            if (order == 1) {
                long v = Long.parseLong(st.nextToken());
                updateRange(1, 0, N - 1, x, y, 1, v);
            } else if (order == 2) {
                long v = Long.parseLong(st.nextToken());
                updateRange(1, 0, N - 1, x, y, v, 0);
            } else if (order == 3) {
                long v = Long.parseLong(st.nextToken());
                updateRange(1, 0, N - 1, x, y, 0, v);
            } else if (order == 4) {
                pw.println(query(1, 0, N - 1, x, y));
            }
        }
        pw.flush();
    }

    static long init(int node, int start, int end) {
        if (start == end) {
            return tree[node] = arr[start];
        }
        int mid = (start + end) / 2;
        return tree[node] = (init(node * 2, start, mid) + init(node * 2 + 1, mid + 1, end)) % MOD;
    }

    static void updateLazy(int node, int start, int end) {
        if (mulLazy[node] == 1 && addLazy[node] == 0) return;

        tree[node] = (tree[node] * mulLazy[node] % MOD + addLazy[node] * (end - start + 1) % MOD) % MOD;

        if (start != end) {
            for (int child : new int[]{node * 2, node * 2 + 1}) {
                mulLazy[child] = mulLazy[child] * mulLazy[node] % MOD;
                addLazy[child] = (addLazy[child] * mulLazy[node] % MOD + addLazy[node]) % MOD;
            }
        }

        mulLazy[node] = 1;
        addLazy[node] = 0;
    }

    static void updateRange(int node, int start, int end, int l, int r, long mul, long add) {
        updateLazy(node, start, end);

        if (r < start || end < l) return;

        if (l <= start && end <= r) {
            mulLazy[node] = mulLazy[node] * mul % MOD;
            addLazy[node] = (addLazy[node] * mul % MOD + add) % MOD;
            updateLazy(node, start, end);
            return;
        }

        int mid = (start + end) / 2;
        updateRange(node * 2, start, mid, l, r, mul, add);
        updateRange(node * 2 + 1, mid + 1, end, l, r, mul, add);
        tree[node] = (tree[node * 2] + tree[node * 2 + 1]) % MOD;
    }

    static long query(int node, int start, int end, int l, int r) {
        updateLazy(node, start, end);

        if (r < start || end < l) return 0;

        if (l <= start && end <= r) return tree[node];

        int mid = (start + end) / 2;
        return (query(node * 2, start, mid, l, r) + query(node * 2 + 1, mid + 1, end, l, r)) % MOD;
    }
}

코드 설명

1. 세그먼트 트리 초기화:

   • init 함수는 초기 배열을 기반으로 세그먼트 트리를 구성한다.

2. 지연 전파:

   • updateLazy 함수는 현재 노드에 적용되지 않은 연산을 수행하고, 자식 노드로 연산을 전파한다.

3. 구간 업데이트:

   • updateRange 함수는 구간에 대한 더하기, 곱하기, 대체 연산을 수행한다.
   • 지연 전파를 활용하여 효율적으로 연산을 수행.

4. 구간 합 쿼리:

   • query 함수는 구간의 합을 MOD로 나누어 반환한다.

So...

이 코드는 지연 전파와 세그먼트 트리를 결합하여 다양한 구간 연산을 효율적으로 처리할 수 있다. 모든 연산은 𝑂(log⁡𝑁) 복잡도로 처리되며, 최대 100,000개의 연산을 빠르게 수행할 수 있다. TIL 작성 중 가장 중요한 부분은 지연 전파를 통해 복잡한 구간 연산을 간단하게 처리했다는 점이다.