TIL: K번째로 작은 가중치 찾기 문제 풀이

문제 설명

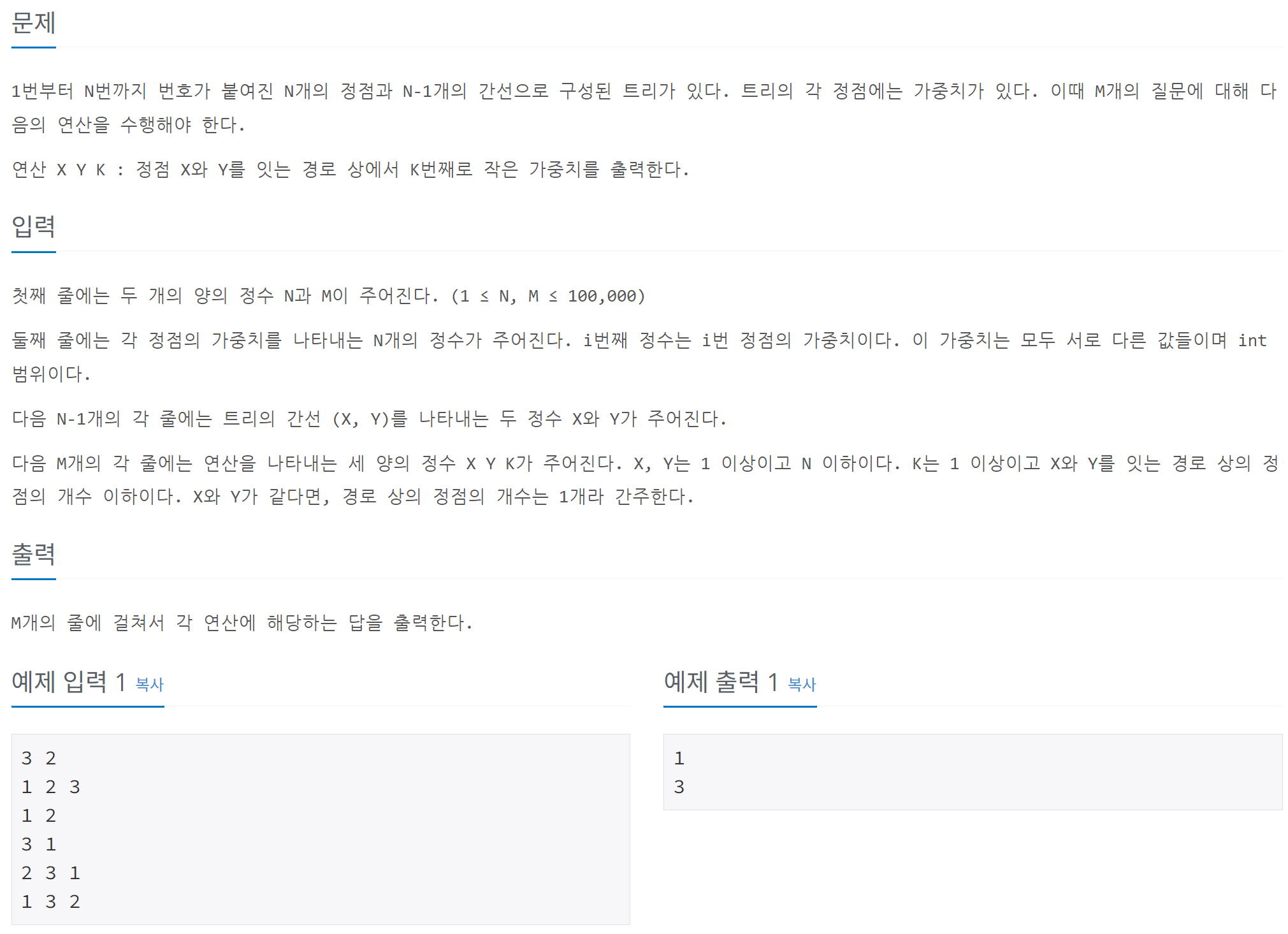
주어진 문제는 트리 구조에서 특정 두 노드 (X)와 (Y)를 잇는 경로 상에서 K번째로 작은 가중치를 찾는 것이다. 이때 트리의 각 정점은 고유한 가중치를 가지며, 입력에는 (N)개의 정점과 (N-1)개의 간선, 그리고 (M)개의 쿼리가 주어진다. 이 문제를 해결하기 위해 HLD(Hierarchical Decomposition) 또는 Segment Tree 기반의 추적이 사용된다.

해결 방법

1. 데이터 구조 선택

   • 트리를 세그먼트 트리의 노드로 표현하여 각 노드에 해당 경로의 누적 정보를 저장한다.
   • 이를 통해 특정 구간의 K번째 값을 효율적으로 탐색할 수 있다.

2. DFS로 트리 정보 구축

   • 트리의 간선 정보를 바탕으로 각 노드의 레벨과 부모 정보를 저장한다.
   • 부모 정보를 기반으로 LCA(최소 공통 조상)를 계산한다.

3. Persistent Segment Tree

   • 각 노드에서의 가중치 정보를 관리하기 위해 Persistent Segment Tree를 사용한다.
   • 이를 통해 트리 경로의 모든 값에 대한 쿼리를 효율적으로 수행한다.

4. 쿼리 처리

   • (X)와 (Y)의 LCA를 찾고, (X)에서 (Y)로 이동하는 경로에 대한 가중치를 확인한다.
   • LCA를 포함한 모든 노드의 정보를 이용해 K번째로 작은 값을 찾아 출력한다.

코드

import java.io.*;
import java.util.*;

public class Main {

    static class Node {
        int value;
        Node left, right;

        Node(int value, Node left, Node right) {
            this.value = value;
            this.left = left;
            this.right = right;
        }

        Node update(int l, int r, int pos) {
            if (pos < l || pos > r) return this;
            if (l == r) return new Node(value + 1, null, null);

            int mid = (l + r) >> 1;
            return new Node(value + 1, 
                left.update(l, mid, pos), 
                right.update(mid + 1, r, pos));
        }
    }

    static final int MAXN = 100001;
    static final int LOG = 17;

    static int[] weights = new int[MAXN];
    static int[] sortedWeights = new int[MAXN];
    static int[] level = new int[MAXN];
    static int[][] parent = new int[MAXN][LOG];
    static List<Integer>[] adj = new ArrayList[MAXN];
    static Node[] roots = new Node[MAXN];
    static Node nullNode;
    static int size;
    static Map<Integer, Integer> weightMap = new HashMap<>();

    static void dfs(int cur, int prev) {
        parent[cur][0] = prev;
        level[cur] = level[prev] + 1;

        roots[cur] = (prev == 0 ? nullNode : roots[prev]).update(1, size, weights[cur]);

        for (int next : adj[cur]) {
            if (next != prev) dfs(next, cur);
        }
    }

    static void preprocessLCA(int n) {
        for (int j = 1; j < LOG; j++) {
            for (int i = 1; i <= n; i++) {
                if (parent[i][j - 1] != 0) {
                    parent[i][j] = parent[parent[i][j - 1]][j - 1];
                }
            }
        }
    }

    static int findLCA(int u, int v) {
        if (level[u] < level[v]) {
            int temp = u;
            u = v;
            v = temp;
        }

        int diff = level[u] - level[v];
        for (int i = 0; i < LOG; i++) {
            if ((diff & (1 << i)) != 0) u = parent[u][i];
        }

        if (u == v) return u;

        for (int i = LOG - 1; i >= 0; i--) {
            if (parent[u][i] != parent[v][i]) {
                u = parent[u][i];
                v = parent[v][i];
            }
        }

        return parent[u][0];
    }

    static int query(Node a, Node b, Node c, Node d, int l, int r, int k) {
        if (l == r) return l;
        int mid = (l + r) >> 1;

        int count = a.left.value + b.left.value - c.left.value - d.left.value;

        if (count >= k) {
            return query(a.left, b.left, c.left, d.left, l, mid, k);
        } else {
            return query(a.right, b.right, c.right, d.right, mid + 1, r, k - count);
        }
    }

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        int n = Integer.parseInt(st.nextToken());
        int m = Integer.parseInt(st.nextToken());

        st = new StringTokenizer(br.readLine());
        for (int i = 1; i <= n; i++) {
            weights[i] = Integer.parseInt(st.nextToken());
            sortedWeights[i] = weights[i];
        }

        Arrays.sort(sortedWeights, 1, n + 1);
        size = 0;
        for (int i = 1; i <= n; i++) {
            if (!weightMap.containsKey(sortedWeights[i])) {
                weightMap.put(sortedWeights[i], ++size);
            }
        }

        for (int i = 1; i <= n; i++) {
            weights[i] = weightMap.get(weights[i]);
        }

        for (int i = 1; i <= n; i++) adj[i] = new ArrayList<>();

        for (int i = 1; i < n; i++) {
            st = new StringTokenizer(br.readLine());
            int u = Integer.parseInt(st.nextToken());
            int v = Integer.parseInt(st.nextToken());

            adj[u].add(v);
            adj[v].add(u);
        }

        nullNode = new Node(0, null, null);
        nullNode.left = nullNode.right = nullNode;

        dfs(1, 0);
        preprocessLCA(n);

        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < m; i++) {
            st = new StringTokenizer(br.readLine());
            int u = Integer.parseInt(st.nextToken());
            int v = Integer.parseInt(st.nextToken());
            int k = Integer.parseInt(st.nextToken());

            int lca = findLCA(u, v);
            int res = query(roots[u], roots[v], roots[lca], (lca == 1 ? nullNode : roots[parent[lca][0]]), 1, size, k);
            sb.append(sortedWeights[res]).append('\n');
        }

        System.out.print(sb);
    }
}

코드 설명

주요 구성 요소

1. Persistent Segment Tree:

   • 세그먼트 트리를 활용해 각 노드의 경로 누적 정보를 관리한다.

2. DFS:

   • 트리의 계층 및 부모 관계를 저장한다.

3. LCA (Lowest Common Ancestor):

   • 두 노드 간의 경로를 구하기 위해 최소 공통 조상을 찾는다.

4. 쿼리 처리:

   • LCA 정보를 기반으로 경로 상의 데이터를 가져오고, 세그먼트 트리에서 K번째 값을 탐색한다.

So...

이 문제는 Persistent Segment Tree와 LCA를 조합한 고난도 알고리즘 문제다. 이를 해결하며 트리 구조와 세그먼트 트리의 통합적 활용법을 배우는 기회가 되었고, 특히 효율적 데이터 관리와 쿼리 최적화 기술에 대한 깊은 통찰을 얻을 수 있었다.