Tree

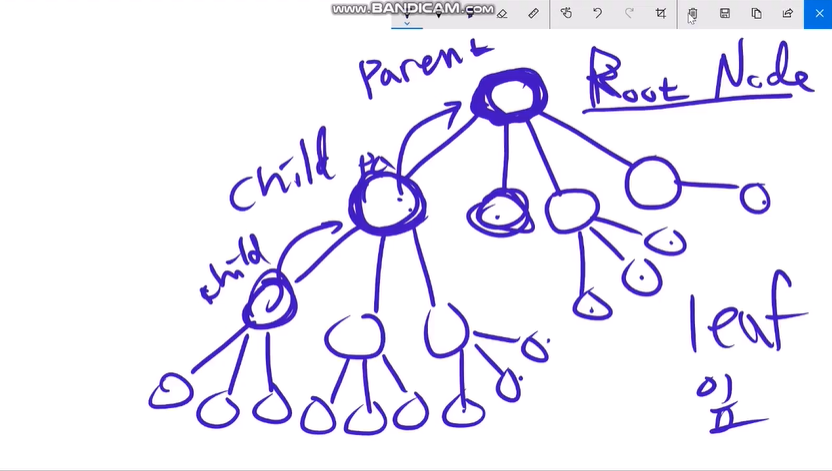
tree는 뿌리인 Root 노드가 있고 그 밑에 Child 노드 들이 있다.
Child 노드의 바로 위의 노드를 Parent 노드라고 하고 상대적인 것이다.
같은 단계에 있는 것 들을 Sibling 이라고 한다.
제일 말단에 Child 노드를 가지지 않는 노드를 Leaf 노드라고 한다.

대표적인 예가 Folder이다.

ex)

package dataStruct

type TreeNode struct {
	Val    int
	Childs []*TreeNode // 포인터형 배열
}

type Tree struct {
	Root *TreeNode
}

func (t *Tree) AddNode(val int) {
	if t.Root == nil {
		t.Root = &TreeNode{Val: val} //루트가 없을 때 루트를 하나 만든다
	} else {
		t.Root.Childs = append(t.Root.Childs, &TreeNode{Val: val}) //루트가 있으면 Childs에 노드를 추가한다.
	}
}

Tree DFS

Depth First Search

깊이 우선 탐색

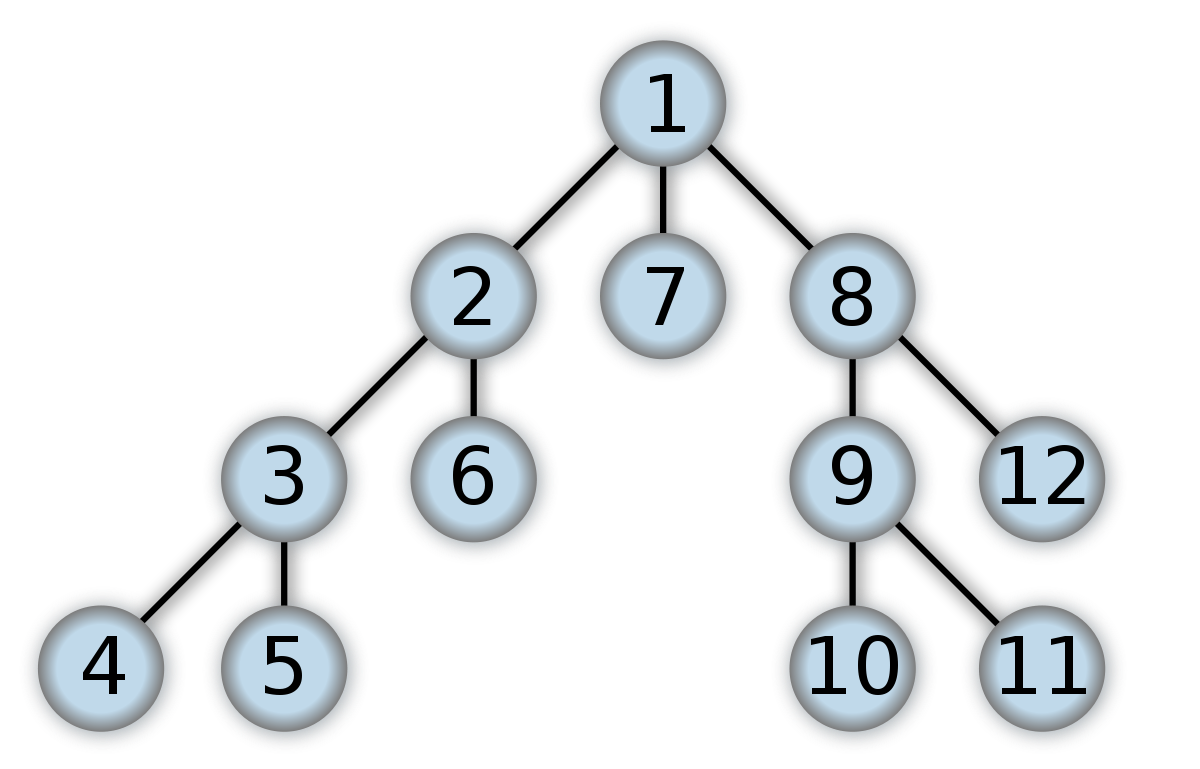
첫번째 child노드에서 그 노드의 child노드 쭉쭉 나가 다가 child노드가 없으면 parent노드로 돌아와서 또다른 child노드 없으면 또 parent로 돌아가서 탐색하는 원리

Dijkstra 알고리즘으로 길찾기
DFS원리를 기반으로 시작노드로 시작해서 자식노드를 따라가서 최소값을 찾아서 최단거리를 찾는 알고리즘

1. 재귀호출을 이용한 방법

ex) package

package dataStruct

import "fmt"

type TreeNode struct {
	Val    int
	Childs []*TreeNode
}

type Tree struct {
	Root *TreeNode
}

func (t *TreeNode) AddNode(val int) { 
	t.Childs = append(t.Childs, &TreeNode{Val: val})
} // child 노드를 추가하는 매소드

func (t *Tree) AddNode(val int) {
	if t.Root == nil {
		t.Root = &TreeNode{Val: val} //루트가 없을 때 루트를 하나 만든다
	} else {
		t.Root.Childs = append(t.Root.Childs, &TreeNode{Val: val}) //루트가 있으면 Childs에 노드를 추가한다.
	}
}

func (t *Tree) DFS1() { // Tree의 매소드
	DFS1(t.Root) // t.Root를 인자로 아래의 함수 DFS1을 콜함
}

func DFS1(node *TreeNode) {
	fmt.Printf("%d->", node.Val) // Val 값 출력

	for i := 0; i < len(node.Childs); i++ { // child노드의 길이 만큼큼
		DFS1(node.Childs[i]) // 재귀 호출
	}
	// childs[0]번째 인덱스 Val = 2 를 출력하고
	// 그 child 노드의 [0]번 째 인덱스를 또 출력 하는 방식
	// 만약 없으면 한단계 위로 올라가서 다른 child 노드를 찾는다
}

ex) main

package main

import (
	"Golesson/dataStruct"
)

func main() {
	tree := dataStruct.Tree{}

	val := 1
	tree.AddNode(val) // Root 를 만듦
	val++             //Val을 증가 시킴 = 2

	for i := 0; i < 3; i++ { // Root의 child 노드에 3개의 노드를 추가
		tree.Root.AddNode(val) // Val = 2 ~ 4 까지의 child 노드가 만들어짐
		val++                  //Val을 증가 시킴 = 3
	}
	for i := 0; i < len(tree.Root.Childs); i++ { // Root의 child 노드를 돌면서
		for j := 0; j < 2; j++ {
			tree.Root.Childs[i].AddNode(val) // 2개 씩 child노드를 추가해줌
			val++
		}
	}

	tree.DFS1() // DFS 탐색을 진행
}
-----------------------------
1->2->5->6->3->7->8->4->9->10->

2. stack을 이용한 방법

ex)

<생략>

func (t *Tree) DFS2() {
	s := []*TreeNode{}    // *TreeNode 슬라이스 생성
	s = append(s, t.Root) // 슬라이스에 Root의 주소 추가

	for len(s) > 0 {
		var last *TreeNode
		last, s = s[len(s)-1], s[:len(s)-1]
		// last = s의 길이 -1  즉 마지막 인덱스 를 last로 초기화
		// 처음 last에 들어가는건 Root
		// s = 0 ~ s의 길이 -1  즉 마지막 인덱스를 제거

		// 2번째 왔을때 s 는 3개가 되고 마지막 인덱스가 last{Val:4}

		// 3번째 왔을때 s 는 2개 마지막 인덱스 last{Val:10}

		fmt.Printf("%d->", last.Val) // 1 -> 4 -> 10

		for i := 0; i < len(last.Childs); i++ {
			s = append(s, last.Childs[i])
			// last.Childs = Root.Childs 만큼 반복 = 3번
			// child 노드를 다시 s로 집어 넣는다. 3개

			// 2번째 last.Childs = 4번째 노드의 Childs개수 만큼 반복 = 2번
			// child 노드를 다시 s로 집어 넣는다. 2개

			// 3번째 last.childs = 10번째 노드의 Childs개수 만큼 반복 = 0번
			// for문은 진행 되지 않고 다시 위로 넘어감
		}
------------------------------------    <생략>    
tree.DFS1()        
-----------------------------------
1->4->10->9->3->8->7->2->6->5->

ex) 순서대로

<생략>
		for i := len(last.Childs)-1; i >= 0; i-- {
			s = append(s, last.Childs[i])
			// 뒤에서 부터가 아닌 순서대로 출력 가능
		}
	}
-------------------------------------
<생략>    
tree.DFS1()        
-----------------------------------
1->2->5->6->3->7->8->4->9->10->

Tree BFS

Breadth First Search

넓이 우선 탐색

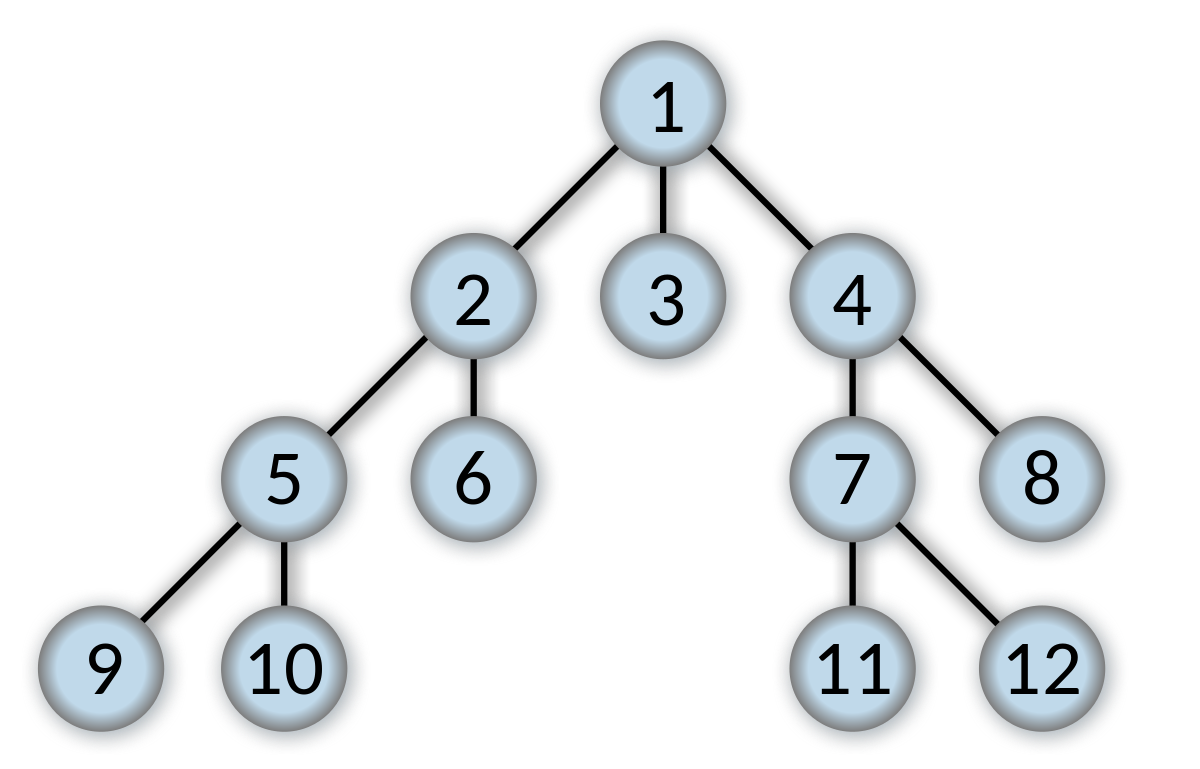
sibling 순서대로 탐색한다.

Queue를 이용한 방법

ex)

<생략>

func (t *Tree) BFS() {
	queue := []*TreeNode{}        //슬라이스 생성
	queue = append(queue, t.Root) // 루트를 넣음

	for len(queue) > 0 {
		var first *TreeNode
		first, queue = queue[0], queue[1:]
		// 맨처음 인덱스를 first로 넣고 queue에서 제거

		// 2번째 돌때 2번째 인덱스를 first로 {Val:2}

		// 3번째 돌때  3번째 인덱스를 first로 {Val:3}

		fmt.Printf("%d->", first.Val) //1->2->

		for i := 0; i < len(first.Childs); i++ {
			queue = append(queue, first.Childs[i])
			// first.Childs = root.childs 만큼 = 3번 반복
			// queue에 root의 child 노드 2번 노드 부터 4번 노드까지 들어감

			// 2번째 queue에 2번 노드의 child 노드 2개 들어감

			// 3번째 queue에 3번 노드의 child 노드가 2개 들어감

			//뒤에 쌓아놓고 선입 선출 하는 방식
		}
	}
}
---------------------------
1->2->3->4->5->6->7->8->9->10->

BST

Binary Search Tree

이진 탐색 트리

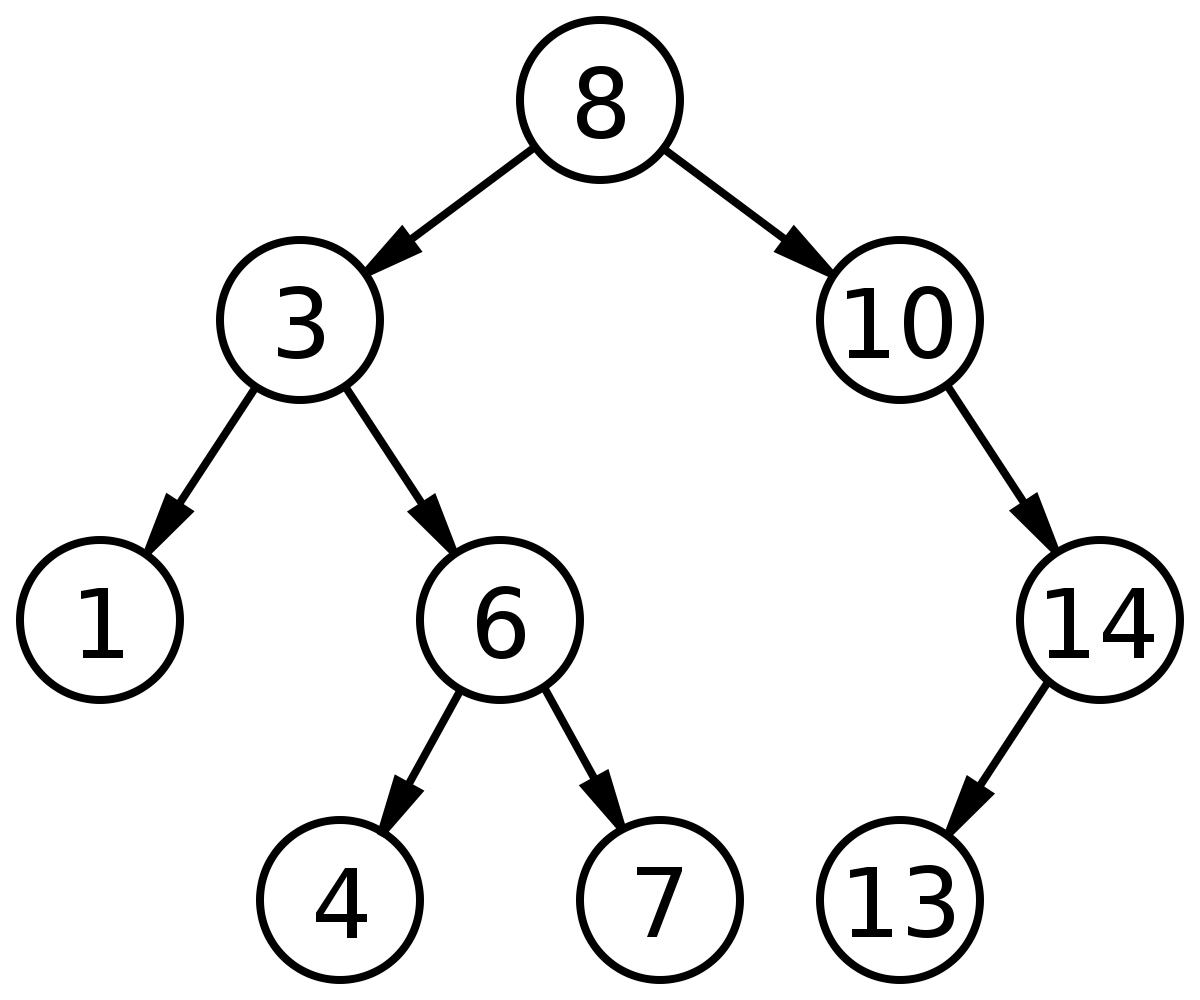
root를 기준으로 왼쪽에는 root의 값보다 작은 값들이 있고 오른쪽에는 큰 값들이 있다.
child로 넘어와서도 똑같이 parent 노드 보다 작은 값들은 왼쪽 큰 값들은 오른쪽에 있다.

DFS나 BFS의 경우 특정 노드를 찾기위해서 해당 노드가 나올때 까지 그전의 모든 노드를 순회해야 한다는 단점이 있다. O(N)

BST의 경우 특정 노드를 찾을때 해당 노드를 부모 노드와 비교하여 작을경우 왼쪽으로 클 경우 오른쪽으로 가서 금방 찾아 낼 수 있다. O(logN)

속도 그래프

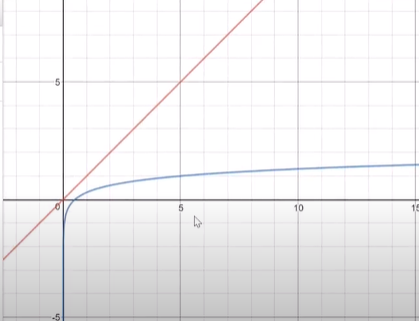
빨강 O(N)
파랑 O(logN)

ex) package

package dataStruct

import "fmt"

type BinaryTreeNode struct {
	Val   int
	left  *BinaryTreeNode
	right *BinaryTreeNode
} // 자식을 2개 밖에 같지 않는 이진 트리

type BinaryTree struct {
	Root *BinaryTreeNode
}

func NewBinaryTree(v int) *BinaryTree {
	tree := &BinaryTree{}
	tree.Root = &BinaryTreeNode{Val: v}
	return tree //Root를 생성하는 함수
}

func (n *BinaryTreeNode) AddNode(v int) *BinaryTreeNode {
	if n.Val > v { // 현재 노드의 Val 보다 작으면
		if n.left == nil { // 왼쪽이 nil 일때
			n.left = &BinaryTreeNode{Val: v} // 왼쪽에 노드 생성해서 주소 저장
			return n.left
		} else { // 왼쪽이 nil이 아닐때
			return n.left.AddNode(v)
			// 재귀 호출로 왼쪽 노드와 비교하여 작으면 해당 노드의 왼쪽에 집어 넣음
		}
	} else { // 현재 노드의 Val 보다 크면
		if n.right == nil { // 오른쪽 값이 nil 일때
			n.right = &BinaryTreeNode{Val: v} // 오른쪽에 노드 생성후 주소 저장
			return n.right
		} else {
			return n.right.AddNode(v)
			// 재귀 호출로 오른쪽 노드와 비교하여 크면 해당 노드의 오른쪽에 집어 넣음
		}
	}
}

type depthNode struct {
	depth int
	node  *BinaryTreeNode
} // 깊이(줄)를 나타내기 위해 만든 구조체

// BFS를 통해 출력하기
func (t *BinaryTree) Print() {
	q := []depthNode{}
	q = append(q, depthNode{depth: 0, node: t.Root})
	currentDepth := 0 // 현재 줄을 나타내기 위한 변수

	for len(q) > 0 {
		var first depthNode
		first, q = q[0], q[1:] // queue 방식을 이용 선입선출

		if first.depth != currentDepth { //현재 줄에 해당 되지 않으면
			fmt.Println() // sibling이 늘 때 마다 띄어쓰기
			currentDepth = first.depth
		}
		fmt.Print(first.node.Val, " ") // 현재 노드의 Val값 출력

		if first.node.left != nil {
			q = append(q, depthNode{depth: currentDepth + 1, node: first.node.left})
			// 현재 노드의 왼쪽 값이 nil이 아닐때 currentDepth +1
			// first.node.left = root.left 값을 집어 넣음
		}
		if first.node.right != nil {
			q = append(q, depthNode{depth: currentDepth + 1, node: first.node.right})
			// 현재 노드의 왼쪽 값이 nil이 아닐때 currentDepth +1
			// first.node.right = root.right 값을 집어 넣음
		}
	}
}

ex) main

package main

import (
	"Golesson/dataStruct"
)

func main() {
	tree := dataStruct.NewBinaryTree(5)
	tree.Root.AddNode(3)
	tree.Root.AddNode(2)
	tree.Root.AddNode(4)
	tree.Root.AddNode(8)
	tree.Root.AddNode(7)
	tree.Root.AddNode(6)
	tree.Root.AddNode(10)
	tree.Root.AddNode(9)

	tree.Print()

}
----------------------------
5
3 8
2 4 7 10
6 9

노드 검색하기

ex) package

<생략>
func (t *BinaryTree) Search(v int) bool {
	return t.Root.Search(v) // bool 값으로 참 거짓을 반환
}

func (n *BinaryTreeNode) Search(v int) bool {
	if n.Val == v { // 찾는값이 현재노드와 같을 경우
		return true // true 반환
	} else if n.Val > v { // 찾는값이 현재 노드보다 작을 경우
		if n.left != nil { // 왼쪽값이 nil 이 아닐때
			return n.left.Search(v) // 계속해서 왼쪽값을 탐색함
		}
		return false // 왼쪽에 더이상 없을 경우 false 숫자가 없다는 얘기
	} else { // 찾는값이 현재노드 보다 클 경우
		if n.right != nil { //오른쪽 값이 nil 이 아닐때
			return n.right.Search(v) // 계속해서 오른쪽 값을 탐색
		}
		return false // 오른쪽에 더이상 없을 경우 false
	}
}

ex) main

<생략>

	if tree.Search(6) {
		fmt.Println("found 6")
	} else {
		fmt.Println("not found 6")
	}
---------------------------------
5 
3 8
2 4 7 10
6 9
found 6

몇번만에 찾았나?

ex) package

func (t *BinaryTree) Search(v int) (bool, int) {
	return t.Root.Search(v, 1) // bool 값으로 참 거짓을 반환, 카운트 초기 값 1
}

func (n *BinaryTreeNode) Search(v int, cnt int) (bool, int) {
	//  검색할 숫자와 현재 카운트를 인자로 받음
	if n.Val == v { // 찾는값이 현재노드와 같을 경우
		return true, cnt // true,cnt 반환
	} else if n.Val > v { // 찾는값이 현재 노드보다 작을 경우
		if n.left != nil { // 왼쪽값이 nil 이 아닐때
			return n.left.Search(v, cnt+1) // 계속해서 왼쪽값을 탐색하고 카운트업
		}
		return false, cnt // 왼쪽에 더이상 없을 경우 false 숫자가 없다는 얘기
	} else { // 찾는값이 현재노드 보다 클 경우
		if n.right != nil { //오른쪽 값이 nil 이 아닐때
			return n.right.Search(v, cnt+1) // 계속해서 오른쪽 값을 탐색하고 카운트업
		}
		return false, cnt // 오른쪽에 더이상 없을 경우 false,cnt
	}
}

ex) main

<생략>
if found, cnt := tree.Search(6); found {
		// Search(6) 함수를 먼저 실행하고 반환값을
		// found, cnt 에 초기화시킨다.
		// ; found 의 값이 true일 경우에 출력한다.
		fmt.Println("found 6 cnt:", cnt)
	} else {
		fmt.Println("not found 6 cnt", cnt)
	}
----------------------------------
5 
3 8
2 4 7 10
6 9
found 6 cnt: 4

BST의 밸런스

binary tree의 뿌리가 만약 순서대로 되어 있다면?

1~10까지의 숫자로 binary tree를 만들었을 경우

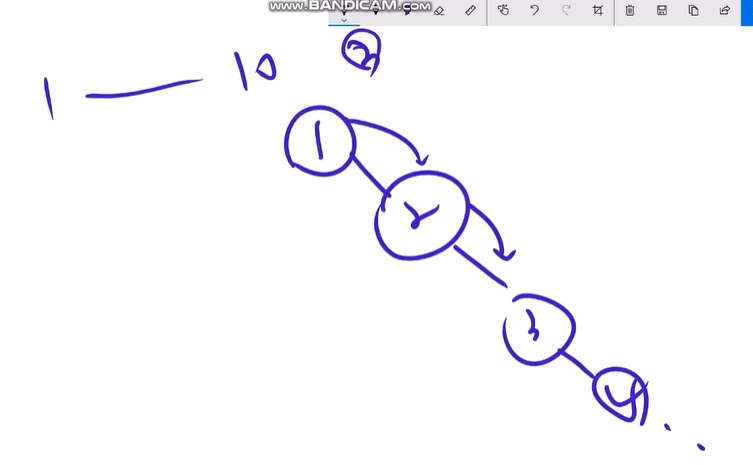
오른쪽으로만 계속 진행된다.

10~1까지의 숫자로 binary tree를 만들었을 경우

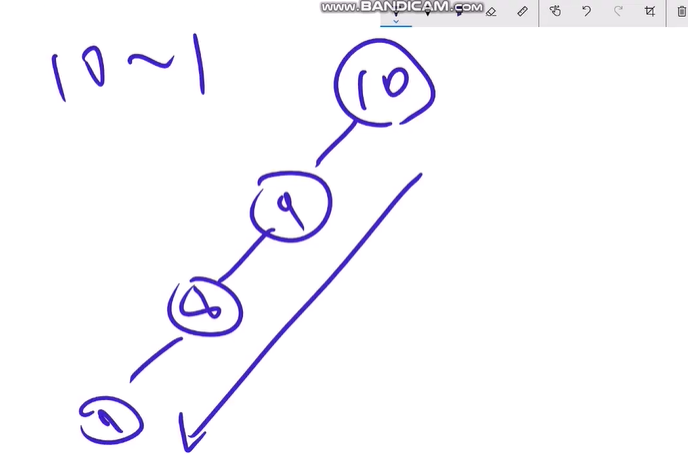
왼쪽으로만 진행 되는것을 볼 수있다.

이런 경우 BST의 장점인 O(logN)이 사라지고 O(N)이 되어 버린다.

그러므로 BST는 중간 값이 위로 올라갈 수록 좋다. 그렇게 되면 높이가 낮아 지게 되는데 BST의 구조는 높이가 낮을 수록 좋다. 이 것을 최소 신장 트리 라고 한다.

Heap

Heap에는 최대힙과 최소힙이 있다.

• 최대힙(MaxHeap): 부모노드 자식노드보다 항상 크거나 같다.

• 최소힙(MinHeap): 부모노드가 자식노드보다 항상 작거나 같다.

• Push: 새로운 노드를 추가하면 맨 밑으로 들어가서 부모 노드와 그 값을 비교하여 최대힙일 때 큰숫자가 위로가고, 최소힙일 때 작은 숫자가 위로 가는 원리이다.

• Pop: 최대힙인 경우 가장 큰 숫자가 먼저 빠지고 맨끝에 노드를 맨위로 올린다. 그 다음 자식 노드와 비교하여 가장 높은 숫자가 위로가고 낮은 숫자는 아래로 내려간다. 최소힙인 경우 반대로 진행 된다.

이러한 원리로 heap을 이용하면 자동적으로 정렬을 할 수 있는데 이것을 Heap 정렬이라고 한다.

*priority queue
우선순위 queue

일반 queue는 선입선출이지만 priority queue는 우선순위가 정해져있고 그 우선순위 부터 빠져나오는 queue이다.

이 priority queue를 구현할 때 Heap을 사용한다.

Max Heap 구현

Heap을 구현할때는 맨위의 노드와 맨끝의 노드를 알아야 하기 때문에 slice를 이용한다.

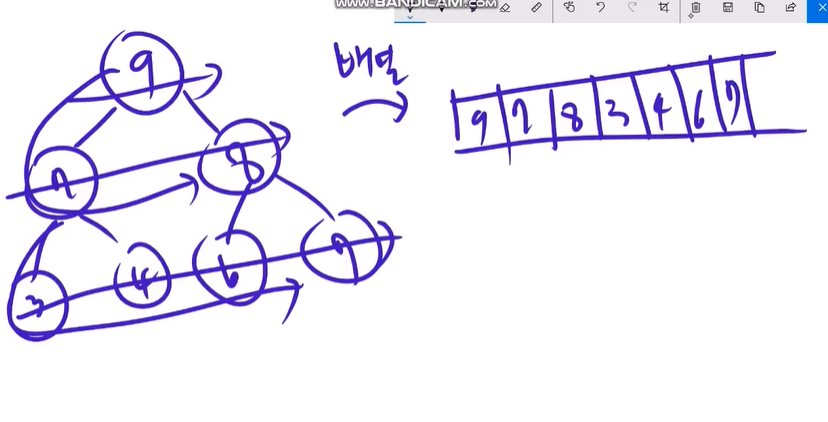
root 부터 BFS 순서대로 slice에 집어 넣는다.
slice의 장점은 현재 노드의 인덱스만 알면 부모 노드와 왼쪽과 오른쪽 자식 노드를 알 수 있다.

N번째 노드 Left = 2N+1
N번째 노드 Right = 2N+2

N번째 부모 = (N-1)/2

ex) push package

package dataStruct

import "fmt"

type Heap struct {
	list []int
}

func (h *Heap) Push(v int) {
	h.list = append(h.list, v) // 인자로 받은 값을 h.list에 append

	idx := len(h.list) - 1 // 현재 인덱스 = 맨 마지막 인덱스
	for idx >= 0 {
		parentIdx := (idx - 1) / 2 //현재 인덱스의 부모 인덱스
		if parentIdx < 0 {
			break
			//만약 부모 인덱스가 마이너스인 경우 즉 부모가 없을 경우 break
		}
		if h.list[idx] > h.list[parentIdx] {
			h.list[idx], h.list[parentIdx] = h.list[parentIdx], h.list[idx]
			// 부모노드와 비교하여 현재노드가 클경우 서로 의 값을 바꿔 줌
			idx = parentIdx
			// 현재 인덱스를 부모인 덱스로 바꿔준다.
		} else {
			break
			// 크지 않을 경우 바꿀 필요가 없기 때문에 바로 break
		}
	}

}

func (h *Heap) Print() {
	fmt.Println(h.list)
}

ex) push main

package main

import (
	"Golesson/dataStruct"
)

func main() {
	h := &dataStruct.Heap{}

	h.Push(9)
	h.Push(8)
	h.Push(7)
	h.Push(6)
	h.Push(5)

	h.Print()

}
-------------------------
[9 8 7 6 5]

ex) pop Package

<생략>
func (h *Heap) Pop() int {
	if len(h.list) == 0 {
		if len(h.list) == 0 {
			return 0
		}
	}

	top := h.list[0]                // 젤위의 노드
	last := h.list[len(h.list)-1]   // 맨 마지막 노드
	h.list = h.list[:len(h.list)-1] // 맨 마지막 노드를 잘라냄

	h.list[0] = last // 맨뒤의 애를 맨위로 바꿈
	idx := 0
	for idx < len(h.list) { // 맨위 부터 끝까지 내려가면서 비교
		swapIdx := -1 // 바꿀 인덱스
		leftIdx := idx*2 + 1
		if leftIdx >= len(h.list) {
			break
			// left 인덱스가 현재 길이보다 길때는 자식 노드가 없다는 말
			// left 인덱스가 없으면 right는 당연히 없다.
		}
		if h.list[leftIdx] > h.list[idx] {
			swapIdx = leftIdx
			// left와 현재값을 비교했을때 left가 더 크면
			// swapIdx 를 leftIdx로 넣고 right와 비교
		}

		rightIdx := idx*2 + 2
		if rightIdx < len(h.list) { // right 노드가 있을 경우
			if h.list[rightIdx] > h.list[idx] { // right 인덱스가 현재값보다 큰 경우
				if swapIdx < 0 || h.list[swapIdx] < h.list[rightIdx] {
					// swapIdx = leftIdx가 0보다 작 거나 , 그값이 right노드 보다 작을떄
					swapIdx = rightIdx // left와 right를 바꿔준다.
				}
			}
		}

		if swapIdx < 0 { // 바꿀 노드가 없을때
			break
		}
		h.list[idx], h.list[swapIdx] = h.list[swapIdx], h.list[idx]
		// 바꿀 노드가 있을 때 스왑
		idx = swapIdx // idx 갱신해서 for문으로
	}
	return top
}

ex) pop main

package main

import (
	"Golesson/dataStruct"
	"fmt"
)

func main() {
	h := &dataStruct.Heap{}

	h.Push(2)
	h.Push(6)
	h.Push(5)
	h.Push(1)
	h.Push(9)

	h.Print()

	fmt.Println(h.Pop())
	fmt.Println(h.Pop())
	fmt.Println(h.Pop())

}
-----------------------------
[9 6 5 1 2] 
9
6
5

Heap을 이용한 문제 풀이

정수 배열(int array)과 정수 N이 주어지면
N번째로 큰 배열 원소를 찾으시오.

예제)
Input: [-1, 3, -1, 5, 4] , 2
Output: 4

Input: [2, 4, -2, -3, 8], 1
Output: 8

Input: [-5, -3, 1], 3
Output: -5

• 작은 원소 배열을 찾을 때 = Max Heap

• 큰 배열 원소를 찾을 때 = Min Heap

원하는 원소가 N번째에 있으면 N개 만큼의 힙을 만들어 top의 값을 뽑아내는 원리

Min Heap

위의 예제는 N번째로 큰 배열의 원소를 찾는 경우이기 때문에 min heap을 통해 풀어본다.

ex) min heap package

package dataStruct

import "fmt"

type Heap struct {
	list []int
}

func (h *Heap) Push(v int) {
	h.list = append(h.list, v) // 인자로 받은 값을 h.list에 append

	idx := len(h.list) - 1 // 현재 인덱스 = 맨 마지막 인덱스
	for idx >= 0 {
		parentIdx := (idx - 1) / 2 //현재 인덱스의 부모 인덱스
		if parentIdx < 0 {
			break
			//만약 부모 인덱스가 마이너스인 경우 즉 부모가 없을 경우 break
		}
		if h.list[idx] < h.list[parentIdx] {
			h.list[idx], h.list[parentIdx] = h.list[parentIdx], h.list[idx]
			// 부모노드와 비교하여 현재노드가 작을 경우 서로의 값을 바꿔 줌
			idx = parentIdx
			// 현재 인덱스를 부모인 덱스로 바꿔준다.
		} else {
			break
			// 크지 않을 경우 바꿀 필요가 없기 때문에 바로 break
		}
	}

}

func (h *Heap) Print() {
	fmt.Println(h.list)
}

func (h *Heap) Count() int {
	return len(h.list)
} // 힙의 갯수를 카운트

func (h *Heap) Pop() int {
	if len(h.list) == 0 {
		if len(h.list) == 0 {
			return 0
		}
	}

	top := h.list[0]                // 젤위의 노드
	last := h.list[len(h.list)-1]   // 맨 마지막 노드
	h.list = h.list[:len(h.list)-1] // 맨 마지막 노드를 잘라냄

	if len(h.list) == 0 {
		return top //자식노드가 없을 경우 리턴
	}

	h.list[0] = last // 맨뒤의 애를 맨위로 바꿈
	idx := 0
	for idx < len(h.list) { // 맨위 부터 끝까지 내려가면서 비교
		swapIdx := -1 // 바꿀 인덱스
		leftIdx := idx*2 + 1
		if leftIdx >= len(h.list) {
			break
			// left 인덱스가 현재 길이보다 길때는 자식 노드가 없다는 말
			// left 인덱스가 없으면 right는 당연히 없다.
		}
		if h.list[leftIdx] < h.list[idx] {
			swapIdx = leftIdx
			// left와 현재값을 비교했을때 left가 더 작으면
			// swapIdx 를 leftIdx로 넣고 right와 비교
		}

		rightIdx := idx*2 + 2
		if rightIdx < len(h.list) { // right 노드가 있을 경우
			if h.list[rightIdx] < h.list[idx] { // right 인덱스가 현재값보다 작은 경우
				if swapIdx < 0 || h.list[swapIdx] > h.list[rightIdx] {
					// swapIdx = leftIdx가 0보다 작 거나 , 그값이 right노드 보다 클떄
					swapIdx = rightIdx // left와 right를 바꿔준다.
				}
			}
		}

		if swapIdx < 0 { // 바꿀 노드가 없을때
			break
		}
		h.list[idx], h.list[swapIdx] = h.list[swapIdx], h.list[idx]
		// 바꿀 노드가 있을 때 스왑
		idx = swapIdx // idx 갱신해서 for문으로
	}
	return top
}

ex) min heap main

package main

import (
	"Golesson/dataStruct"
	"fmt"
)

func main() {
	h := &dataStruct.Heap{}

	//Input: [-1, 3, -1, 5, 4] , 2
	//Output: 4
	nums := []int{-1, 3, -1, 5, 4}

	for i := 0; i < len(nums); i++ {
		h.Push(nums[i])
		if h.Count() > 2 { // 힙의 갯수를 2개로 제한함
			h.Pop() // 2개가 넘어가면 빼냄
		}
	}
	fmt.Println(h.Pop())

	// Input: [2, 4, -2, -3, 8], 1
	// Output: 8
	h = &dataStruct.Heap{}

	nums = []int{2, 4, -2, -3, 8}

	for i := 0; i < len(nums); i++ {
		h.Push(nums[i])
		if h.Count() > 1 { // 힙의 갯수를 1개로 제한함
			h.Pop() // 1개가 넘어가면 빼냄
		}
	}
	fmt.Println(h.Pop())

	// Input: [-5, -3, 1], 3
	// Output: -5
	h = &dataStruct.Heap{}

	nums = []int{-5, -3, 1}

	for i := 0; i < len(nums); i++ {
		h.Push(nums[i])
		if h.Count() > 3 { // 힙의 갯수를 3개로 제한함
			h.Pop() // 3개가 넘어가면 빼냄
		}
	}
	fmt.Println(h.Pop())
}