병합정렬

병합정렬

• 여러 개의 정렬된 자료의 집합을 병합하여 한 개의 정렬된 집합으로 만드는 방식
• 분할 정복 알고리즘 활용
  1) 자료를 최소 단위의 문제까지 나눈 후에 차례대로 정렬하여 최종 결과를 얻어냄
  2) top-down 방식
  3) 안정 정렬
• 시간 복잡도 : O(n log n)

병합 정렬 과정

1. 분할 단계: 전체 자료 집합에 대하여, 최소 크기의 부분집합이 될 때까지 분할 작업을 계속한다. 👉 mergeSort( )
2. 병합 단계: 2개의 부분 집합을 정렬하면서 하나의 집합으로 병합
   (8개의 부분집합이 1개로 병합될 때까지 반복함) 👉 merge( )

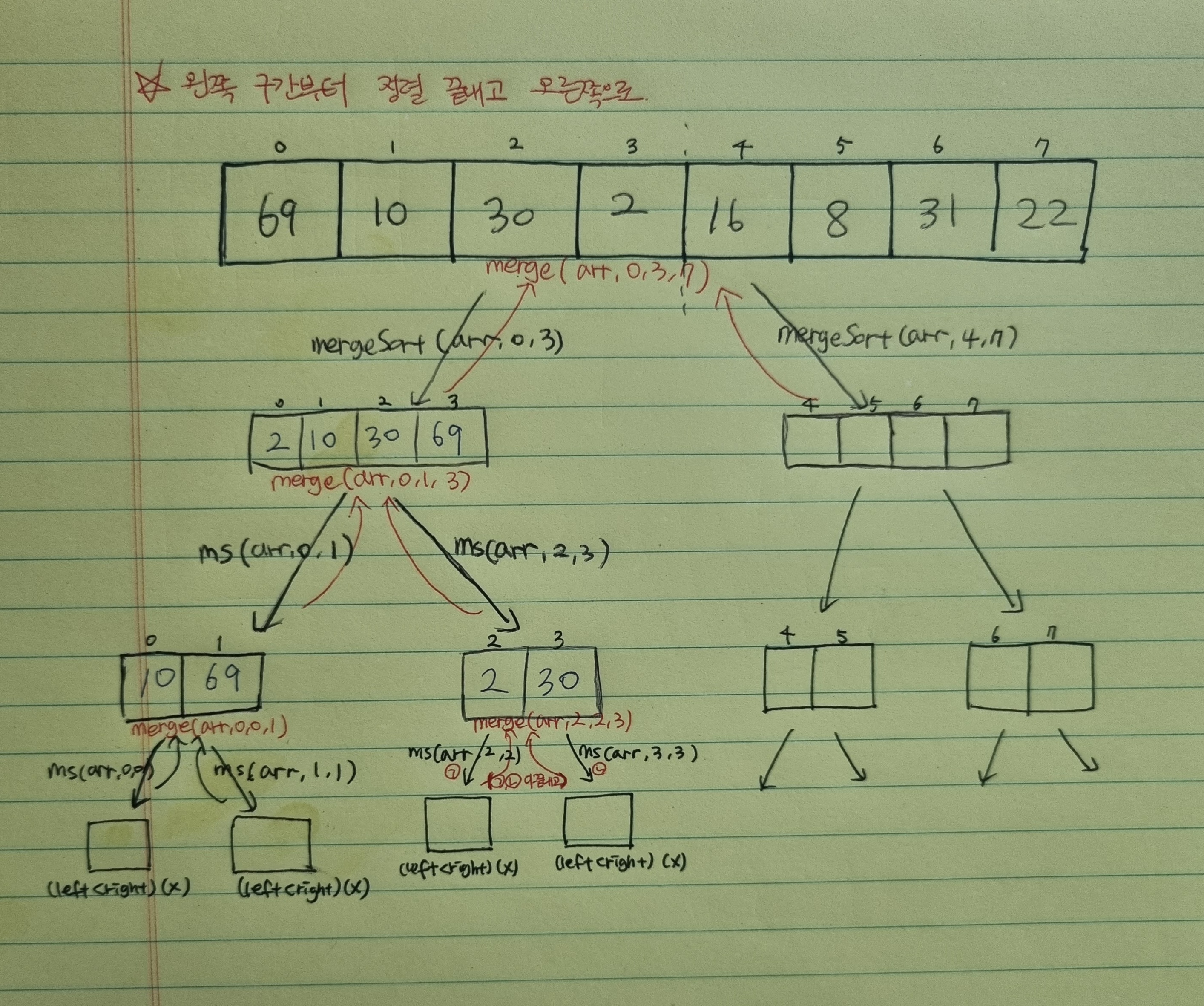
병합 정렬 구현

import java.util.Arrays;

public class MergeSort {
	
	static int[] sortedArr;
	public static void main(String[] args) {
		int[] arr = { 77, 32, 37, 17, 22, 8, 13, 42 };
		sortedArr = new int[arr.length];

		System.out.println("정렬전: " + Arrays.toString(arr));
		mergeSort(arr, 0, arr.length-1);
		System.out.println("정렬후: " + Arrays.toString(arr));
	}

	public static void mergeSort(int[] arr, int left, int right) {
		if (left < right) {					
			int mid = (left + right) / 2;
			mergeSort(arr, left, mid); 					// 왼쪽 절반 분할
			mergeSort(arr, mid + 1, right);				// 오른쪽 절반 분할
			merge(arr, left, mid, right); 				// 정렬하면서 병합
		}
	}

	public static void merge(int[] arr, int left, int mid, int right) {
		int L = left; 									// 왼쪽 구간 시작 인덱스
		int R = mid + 1; 								// 오른쪽 구간 시작 인덱스
		int idx = left; 								// 정렬완료한 원소를 저장할 위치

		// 서로 구간의 값이 남아있는 경우 비교하면서 집어넣기
		while (L <= mid && R <= right) {
			if (arr[L] <= arr[R])						// = (등호)가 있어야 안정정렬
				sortedArr[idx++] = arr[L++];
			else
				sortedArr[idx++] = arr[R++];
		}

		// 왼쪽 구간이 남았다면
		if (L <= mid) {
			for (int i = L; i <= mid; i++)
				sortedArr[idx++] = arr[i];
		}
		// 오른쪽 구간이 남았다면
		else {
			for (int i = R; i <= right; i++)
				sortedArr[idx++] = arr[i];
		}

		// 정렬한 임시배열을 원 배열에 저장한다.
		for (int i = left; i <= right; i++)
			arr[i] = sortedArr[i];

//		System.out.println(Arrays.toString(arr));
	}
}