부분집합 | 반복문

부분집합

1. 반복문
2. 재귀함수
3. 비트마스킹

부분집합

자기자신과 공집합을 포함한 모든 부분집합(power set)의 개수는 2^n개이다.

---

import java.util.Arrays;

public class 부분집합_반복문 {

	public static void main(String[] args) {

		// 4가지 원소의 부분집합
		// 0이면 선택X, 1이면 선택
		int N = 4;
		int[] visited = new int[N];

		for (int i = 0; i < 2; i++) {
			visited[0] = i;
			for (int j = 0; j < 2; j++) {
				visited[1] = j;
				for (int k = 0; k < 2; k++) {
					visited[2] = k;
					for (int l = 0; l < 2; l++) {
						visited[3] = l;
						System.out.println(Arrays.toString(visited));
					}
				}
			}
		}

	}

}

---

결과

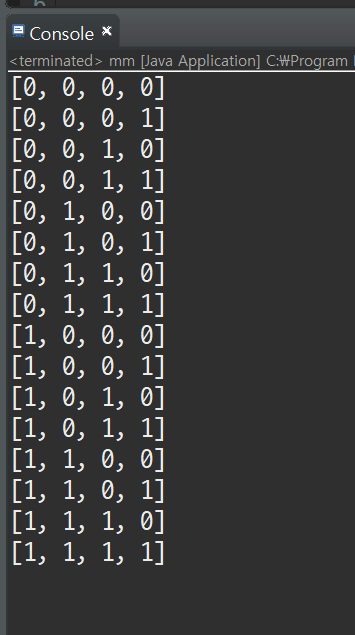
자기자신과 공집합을 포함한 모든 경우의 부분집합을 확인할 수 있다. 이 때 0은 선택하지 않은 상태, 1은 선택한 상태를 뜻하므로 어떤 경우에 어떤 원소들을 가지고 있는지까지 확인할 수 있다.
이는 비트마스킹에 활용할 수 있다. 0~15까지의 수(2^n)를 이진수로 표현하고 있다.
다만 반복문으로 부분집합을 구할 때는 원소가 하나씩 늘어날 때마다 반복문도 하나씩 추가해야한다.

---