
문제 설명
주어진 숫자 중 3개의 수를 더했을 때 소수가 되는 경우의 개수를 구하려고 합니다. 숫자들이 들어있는 배열 nums가 매개변수로 주어질 때, nums에 있는 숫자들 중 서로 다른 3개를 골라 더했을 때 소수가 되는 경우의 개수를 return 하도록 solution 함수를 완성해주세요.
제한사항
- nums에 들어있는 숫자의 개수는 3개 이상 50개 이하입니다.
- nums의 각 원소는 1 이상 1,000 이하의 자연수이며, 중복된 숫자가 들어있지 않습니다.
입출력 예
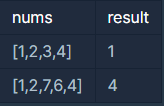
입출력 예 설명
입출력 예 #1
[1,2,4]를 이용해서 7을 만들 수 있습니다.
입출력 예 #2
[1,2,4]를 이용해서 7을 만들 수 있습니다.
[1,4,6]을 이용해서 11을 만들 수 있습니다.
[2,4,7]을 이용해서 13을 만들 수 있습니다.
[4,6,7]을 이용해서 17을 만들 수 있습니다.
풀이
우선, 조합의 경우의 수를 다 찾는다.
예를 들어 [1, 2, 3]의 배열에서 2개를 고른다면
1을 선택하면[2, 3]중에서 1개씩 선택하여 조합을 구하고나면[1, 2], [1, 3]가 나오게 되고
2를 선택하면[3]중에서 1개씩 선택하여 조합을 구하고나면[2, 3]가 나오게 된다.
3을 선택하면[]중에서 1개씩 선택해야 하지만 고를 수 있는 수가 부족하기 때문에 나올 조합이 없게 된다.
위의 방법을 코드화하여 getCombination 함수 재귀를 이용하자면 마지막 1개를 고를 때 재귀 종료 조건을 걸었고
기존의 배열의 순회하면서 숫자 처음을 고르고 나머지를 slice하여 재귀호출하였고
그리고 다시 처음 골랐던 숫자와 재귀 호출하여 나온 값들이랑 concat 시켜주었다.
[1, 2, 3]의 배열 중 2개를 고를 때
getCombination( [1, 2, 3], 2 )
num= 1
restArr= [2, 3]getCombination( [2, 3], 2 - 1 )
재귀 종료return [[2], [3]]
combinations= [[2], [3]]
concatArr= [[1, 2], [1, 3]]
spread operator이용하여
result.push( [1, 2], [1, 3] )
조합이 구해지고 나면 reduce함수를 통해 각 배열의 합을 구해주었고 [3, 4]
해당 배열의 소수를 판별하여 카운트해주었다.
function solution(nums) {
let answer = 0;
const primeCount = (arr) => {
arr.map( num => {
for(let i=2; i<= num/2; i++){
if(num % i === 0) return;
}
answer++;
});
};
const getCombination = (arr, selectNum) => {
let result = [];
if(selectNum === 1) return arr.map( num => [num]);
arr.map( (num, idx, origin) => {
let restArr = origin.slice(idx + 1);
let combinations = getCombination(restArr, selectNum - 1);
let concatArr = combinations.map( combination => [num, ...combination]);
result.push(...concatArr);
});
return result;
};
const combinations = getCombination(nums, 3);
const addedList = combinations.map( combination => combination.reduce( (acc,cur) => acc + cur, 0));
primeCount(addedList);
return answer;
}