[자료구조] 힙(Heap)

zzzzsb·2022년 7월 20일

자료구조&알고리즘

목록 보기

4/8

힙(Heap)

힙은 완전 이진트리 기반의 자료구조로, 우선순위 큐를 구현하는데 사용된다.
트리 구조이기 때문에 삽입과 삭제에 O(logN)의 시간이 소요된다.

힙의 종류

힙의 종류에는 최대힙, 최소힙이 있다.
힙을 통해 최댓값이나 최솟값을 찾는 연산을 빠르게 수행할 수 있다.

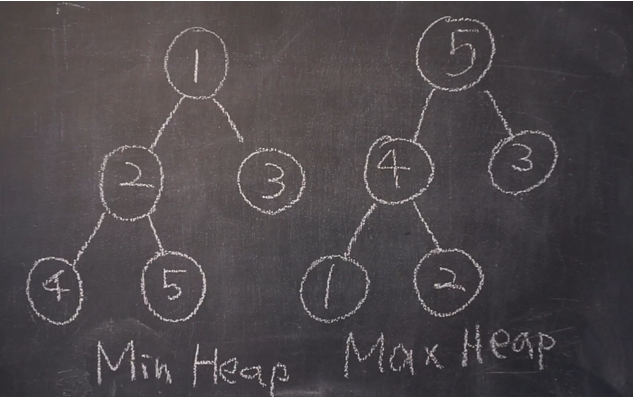
최대 힙(Max-Heap)

트리의 root 노드에 가장 큰 값이 위치해 있다.
부모노드가 자식노드 보다 항상 크거나 같은 값을 가진다.

최소 힙(Min-Heap)

트리의 root 노드에 가장 작은 값이 위치해 있다.
부모노드가 자신노드 보다 항상 작거나 같은 값을 가진다.

힙 구현 with Javascript

자바스크립트 외의 다른 언어에서는 힙 구조 자체를 기본 라이브러리로 제공해주는 경우가 많다.
- Java, C++의 경우 PriorityQueue를 라이브러리로 제공해준다...ㅎ
- Python3의 경우 heapq, heapify 함수 등으로 힙 구조화가 가능하다
- 물론, 코딩테스트 외의 경우라면 자바스크립트도 외부 라이브러리를 통해 힙을 사용할 수 있다.

아무튼, 자바스크립트에서는 힙을 기본 라이브러리로 제공하지 않기에, 직접 구현해서 사용해야한다!

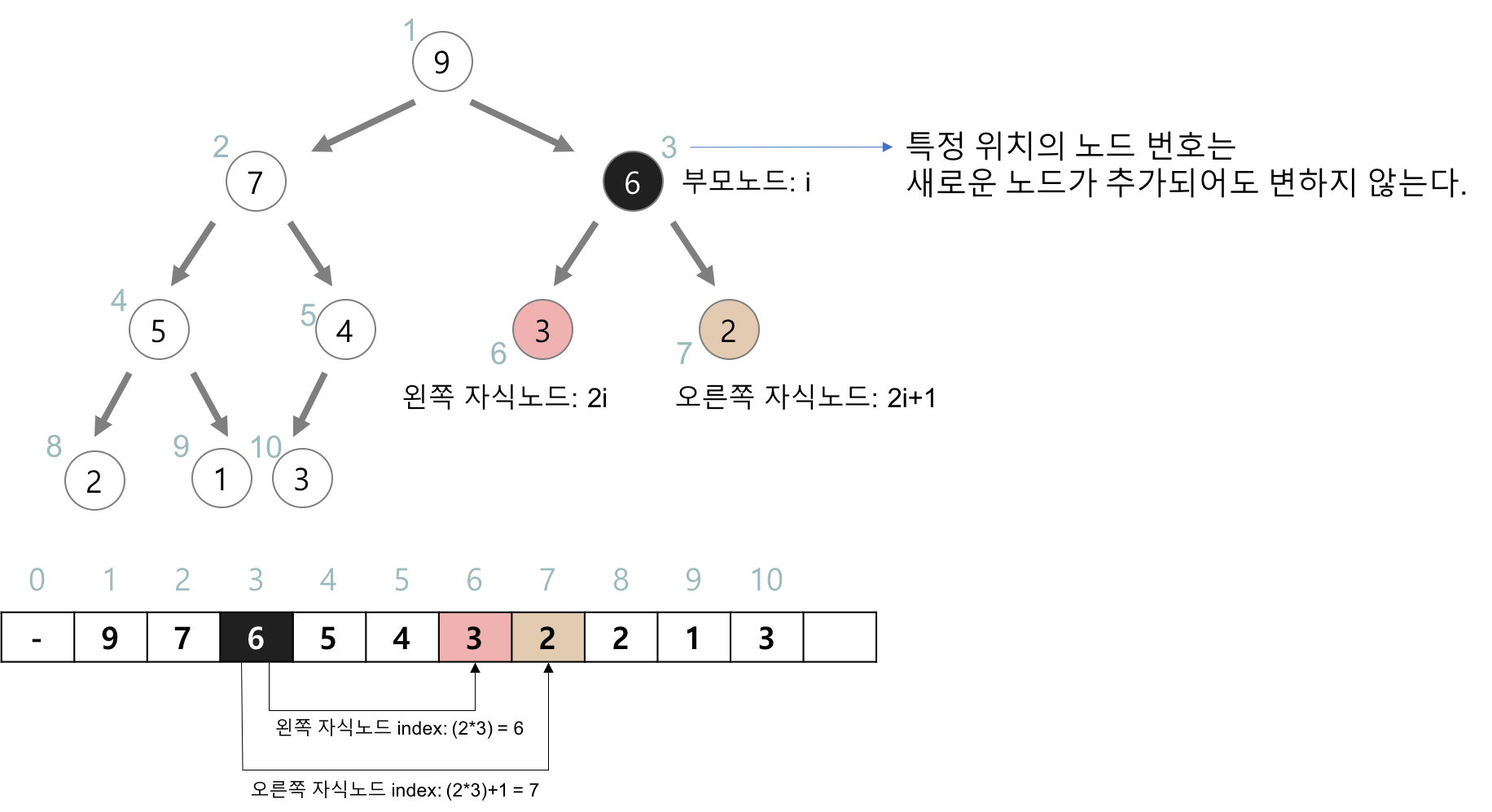
힙을 구현하는 표준적인 자료구조는 배열이다.
구현을 쉽게 하기 위해(계산의 편의성) 배열의 첫번째 인덱스인 0은 사용하지 않는다.
힙은 완전 이진트리 기반의 자료구조이지만, 보통의 완전 이진트리와 다르게 반정렬 상태(느슨한 정렬 상태)를 유지한다.
- 최대 힙이라면 큰 값이 부모노드에, 최소 힙이라면 작은 값이 부모노드에 배치되는 것만 유지
- 왼쪽-오른쪽 자식노드는 부모 노드보다 작은 값을 유지하기만 하면 됨

힙에서 부모 노드 - 자식 노드의 관계

왼쪽 자식 index = (부모 index) * 2

오른쪽 자식 index = (부모 index) * 2 + 1

부모 index = Math.floor(자식 index) / 2

전체 코드 - 삽입&삭제

class MinHeap {
    constructor() {
        this.heap = [ null ];
    }
    
    size() {
        return this.heap.length - 1;
    }
    
    getMin() {
        return this.heap[1] ? this.heap[1] : null;
    }
    
    swap(a, b) {
        [ this.heap[a], this.heap[b] ] = [ this.heap[b], this.heap[a] ];
    }
    
    heappush(value) {
        this.heap.push(value);
        let curIdx = this.heap.length - 1;
        let parIdx = (curIdx / 2) >> 0;
        
        while(curIdx > 1 && this.heap[parIdx] > this.heap[curIdx]) {
            this.swap(parIdx, curIdx)
            curIdx = parIdx;
            parIdx = (curIdx / 2) >> 0;
        }
    }
    
    heappop() {
        const min = this.heap[1];	
        if(this.heap.length <= 2) this.heap = [ null ];
        else this.heap[1] = this.heap.pop();   
        
        let curIdx = 1;
        let leftIdx = curIdx * 2;
        let rightIdx = curIdx * 2 + 1; 
        
        if(!this.heap[leftIdx]) return min;
        if(!this.heap[rightIdx]) {
            if(this.heap[leftIdx] < this.heap[curIdx]) {
                this.swap(leftIdx, curIdx);
            }
            return min;
        }

        while(this.heap[leftIdx] < this.heap[curIdx] || this.heap[rightIdx] < this.heap[curIdx]) {
            const minIdx = this.heap[leftIdx] > this.heap[rightIdx] ? rightIdx : leftIdx;
            this.swap(minIdx, curIdx);
            curIdx = minIdx;
            leftIdx = curIdx * 2;
            rightIdx = curIdx * 2 + 1;
        }

        return min;
    }
}