[#1] LORA: LOW-RANK ADAPTATION OF LARGE LANGUAGE MODELS

영상을 보고 정리해보는 LoRA ~
🔆 Low-rank Adaptation == LoRA

KEY IDEA

• PEFT의 기술 중 하나이다.
• 어떻게 효율적으로 파라미터 수를 줄이며 파인튜닝을 진행하게 되냐면, 원래 모델의 가중치들은 동결하고 low-rank를 갖는 행렬들을 새로 정의하여 그 행렬의 파라미터들만 업데이트하도록 한다.

INTUITION

• 일반적으로 가중치 행렬은 full-rank를 갖지만, 어떤 특정 태스크에서는 사전 훈련된 모델의 웨이트 행렬이 낮은 “intrinsic rank”를 갖는다는 연구(Aghajanyan et al. (2020))가 있었다.
• 따라서 이러한 사전 연구에 기반하여, LoRA 논문에서는 가중치에 대한 업데이트도 어댑테이션 과정에서 low-rank를 갖는다고 가정한다.

😲 랭크가 뭔데요? 🤓 수학적 설명 w/예시

METHOD

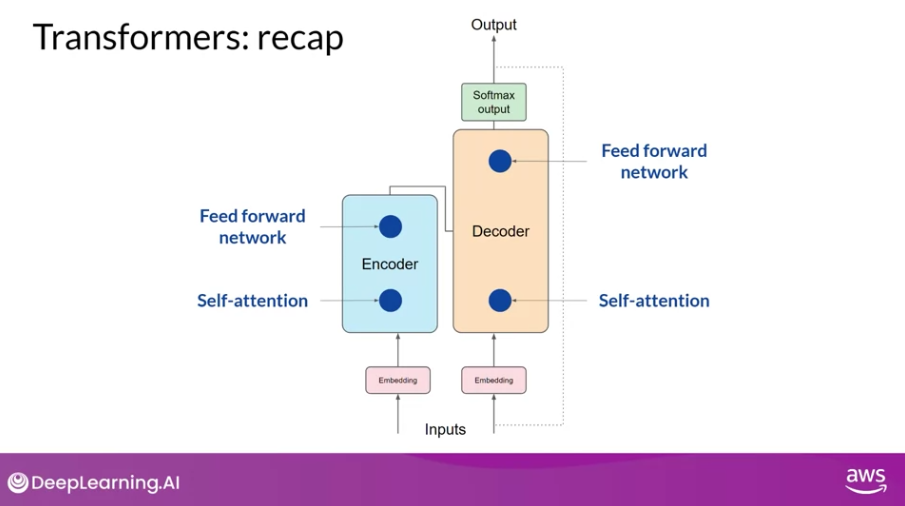
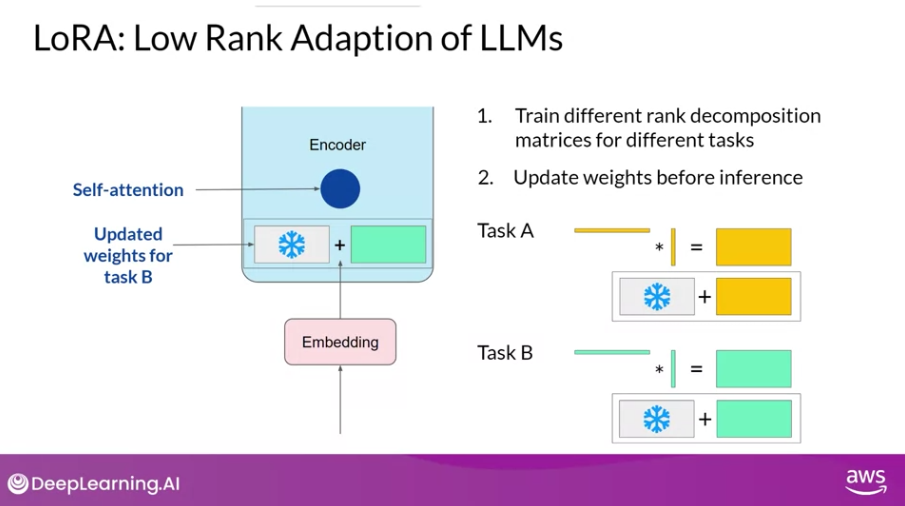
• 예를 들면, 우리가 잘 아는 트랜스포머는 인코더/디코더가 있고 각각은 self-attention과 feedforward를 포함하고 있는 구조이다.
• 사전 학습을 진행하면 이 네트워크들의 웨이트가 업데이트 될 것이다.
  

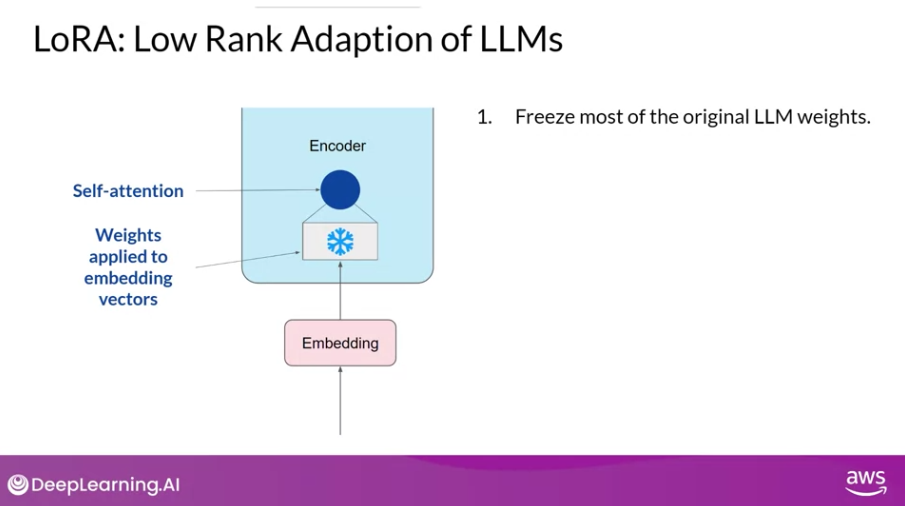
• 이 때, LoRA는 이러한 원래 모델의 파라미터들을 동결하고, 파인튜닝 과정에서 원래 모델의 가중치는 그대로 두고, low-rank decomposition 행렬 쌍을 추가로 주입하게 된다.
• 이 때 주입되는 행렬들은 원래 모델의 웨이트 행렬과 차원이 같도록 설정한다. (추후 웨이트 행렬을 만들어야 하니까!)

절차를 살펴보면 다음과 같다.

1. 원래 모델의 파라미터들을 고정한다. 원래 모델의 웨이트에 대해서는 오직 read만 수행하며, 백프로파게이션 등을 수행하지 않는다.
   

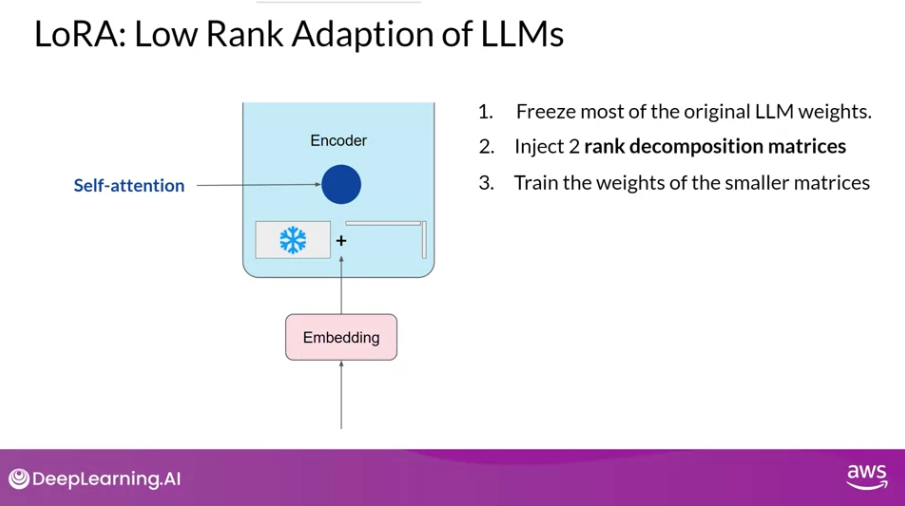
2. 동일한 지도 학습 프로세스를 사용하여 한 쌍의 low-rank decomposition 행렬을 주입하고, 훈련한다 (사진 상에서는 2~3 step)
   

3. 인퍼런스 과정에서는, 한 쌍의 행렬을 곱하여, 고정해두었던 원래 모델의 파라미터와 같은 크기의 행렬을 만든다음, 두 행렬을 더하여 업데이트한다.
   

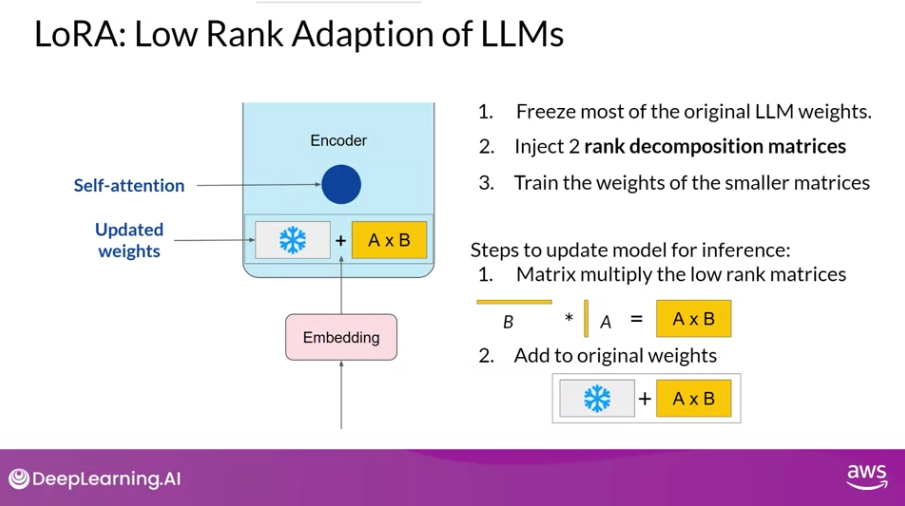
• 추가로, 피드포워드 네트워크에서도 LoRA가 적용될 수도 있지만, 보통은 위의 예시처럼 셀프어텐션 레이어세만 적용되는 경우가 많다고 한다.
  • 대부분의 파라미터가 셀프어텐션 레이어에 존재하기 때문이다.

장점

• full-finetune 과정에서 요구하는 것보다 훨씬 적은 파라미터를 사용한다.
• 그만큼 저장공간도 덜 필요하게 되고,
• 백프로파게이션 속도도 빨라지게 된다.
• 또한, 적은 연산량을 가지고도 full-finetune 기법과 비견할 만한 성능을 낼 수 있다 (논문 실험 섹션에 정리되어 있음).

• 실제 사용하는 입장에서는, 연산량이 기존 LLM의 15~20%로 줄어들기 때문에, 단일 GPU에서도 학습할 수 있다.

웨이트 파라미터에 대해서 자세히 보게 되면, 영상에서는 예를 들어 설명하고 있다.
만약 Attention is All You Need 논문에서 사용한 트랜스포머 아키텍처를 사용하고, rank는 8로 설정한다고 가정해보자.

• 위와 같이 원래는 $d*k = 512*64 = 32,768$ 의 파라미터가 필요하지만, 랭크가 8인 LoRA에서는 두두 쌍의 행렬들이 각각 $r*k=8*64=512$, $d*r=512*8=4,096$의 파라미터가 필요하기 때문에 도합 4,608개의 파라미터만 사용하면 된다.
  => 즉, 파라미터 수를 86%나 감소시킬 수 있다!

또한, 태스크를 여러개 수행하는 상황에서도, full-finetuning을 사용했을 때 처럼 개별 태스크에 대한 모델을 각각 정의할 것이 아니라, LoRA 매트릭스 값만 업데이트 해주면 되니, 메모리 측면에서 상당히 효율적이다.

한계

• low-rank approximation process에서 모델 성능에 영향을 미칠 수 있는 정보 손실이 일어날 수 있다. 연산량과 성능의 트레이드 오프 ..

• 논문의 실험 파트에서도 볼 수 있듯, 랭크를 얼마로 설정하냐가 성능에 큰 영향을 끼친다. 따라서 랭크 값을 잘 설정하는 것이 중요하다.

코드

👉 github link : 마이크로 소프트에서 제공하는 오피셜 코드

• 토치의 nn.Linear, nn.Embedding, nn.Conv2d을 대체할 수 있는 클래스들을 loralib/에서 각각 제공하고 있다.
• 여기에 추가로 일부 Attention qkv 프로젝션 구현과 같이 단일 nn.Linear가 둘 이상의 레이어를 나타내는 경우를 위하여 nn.MergedLinear도 제공하고 있다.

• class Embedding(nn.Embedding, LoRALayer) : PyTorch의 nn.Embedding 모듈을 상속받아 LoRA 레이어를 추가한 클래스를 대표로 살펴보면 다음과 같다.

class Embedding(nn.Embedding, LoRALayer):
    # LoRA implemented in a dense layer
    def __init__(
        self,
        num_embeddings: int,
        embedding_dim: int,
        r: int = 0,
        lora_alpha: int = 1,
        merge_weights: bool = True,
        **kwargs
    ):
        nn.Embedding.__init__(self, num_embeddings, embedding_dim, **kwargs)
        LoRALayer.__init__(self, r=r, lora_alpha=lora_alpha, lora_dropout=0,
                           merge_weights=merge_weights)
                           
        # Actual trainable parameters
        # LoRA 레이어에 대한 학습 가능한 가중치(한 쌍의 low-rank 분해 행렬) 를 초기화 함
        if r > 0:
            self.lora_A = nn.Parameter(self.weight.new_zeros((r, num_embeddings)))
            self.lora_B = nn.Parameter(self.weight.new_zeros((embedding_dim, r)))
            self.scaling = self.lora_alpha / self.r
            # Freezing the pre-trained weight matrix
            self.weight.requires_grad = False
        self.reset_parameters()

    def reset_parameters(self):
    	# 임베딩 레이어의 가중치를 초기화
        nn.Embedding.reset_parameters(self)
        if hasattr(self, 'lora_A'):
            # initialize A the same way as the default for nn.Linear and B to zero
            nn.init.zeros_(self.lora_A)
            nn.init.normal_(self.lora_B)

    def train(self, mode: bool = True):
        nn.Embedding.train(self, mode)
        if mode:
            if self.merge_weights and self.merged:
                # Make sure that the weights are not merged
                if self.r > 0:
                    self.weight.data -= (self.lora_B @ self.lora_A).transpose(0, 1) * self.scaling
                self.merged = False
        else:
            if self.merge_weights and not self.merged:
                # Merge the weights and mark it
                if self.r > 0:
                    self.weight.data += (self.lora_B @ self.lora_A).transpose(0, 1) * self.scaling
                self.merged = True
        
    def forward(self, x: torch.Tensor):
        if self.r > 0 and not self.merged:
            result = nn.Embedding.forward(self, x)
            after_A = F.embedding(
                x, self.lora_A.transpose(0, 1), self.padding_idx, self.max_norm,
                self.norm_type, self.scale_grad_by_freq, self.sparse
            )
            result += (after_A @ self.lora_B.transpose(0, 1)) * self.scaling
            return result
        else:
            return nn.Embedding.forward(self, x)

• 먼저 학습가능한 두 쌍의 low-rank 분해 행렬 lora_A와 lora_B을 입력받은 차원 관련 파라미터에 맞게 초기화한다.
• reset_parameters : 행렬 lora_A와 lora_B을 초기화한다. 이 때, 논문과 동일하게 0과 가우시안 분포로 초기화한다.
  • $d*k$ 의 웨이트를 분해하여 $r*k = (r, num\_embeddings)$과 $d*r = (embedding\_dim, r)$ 의 크기를 갖는 행렬로 쪼갠다.
• train : 파라미터(mode, merged)에 따라서, weight를 업데이트 하거나 복원을 한다.
  • 웨이트를 계산하는 것 자체는, self.weight.data += (self.lora_B @ self.lora_A).transpose(0, 1) * self.scaling 이렇게 표현된다. 행렬 곱을 하고 scaling을 해준 다음, 원래 웨이트와 더한다. 간단.
• forward : 입력이 들어오면 임베딩을 넘겨주는 포워드 패스 연산을 정의하고 있다.
  • 만약에 파인튜닝이 완료되지 않은 경우에는 (if문), nn.Embedding.forward(self, x)를 통해 기존의 임베딩 레이어를 사용하여 result를 계산한다.
  • 그 다음, F.embedding을 통해 입력 x와 self.lora_A (파인튜닝된 파라미터)의 임베딩 결과인 after_A를 계산한다.
  • 마지막으로, 위의 결과와 self.lora_B을 행렬곱하여 최종 아웃풋을 뽑아내게 된다.

---

Reference

• Paper(arxiv)
• 코세라 강의 : 모든 이미지와 전반적인 설명을 가져왔다.
• Youtube 영상 : 이해를 도와주는 좋은 영상