
정렬 알고리즘의 종류와 개념
선택 정렬
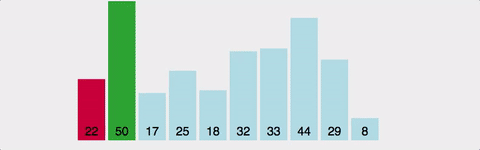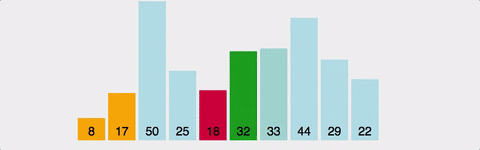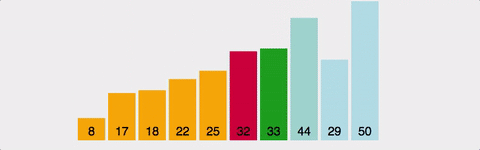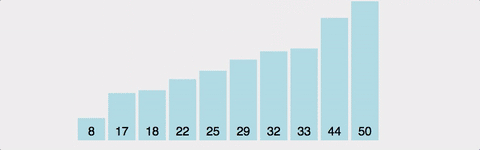
정렬되지 않은 부분을 쫙 돌면서 제일 작은애(혹은 제일 큰 애)를 선택해서 위치 바꾸기. 시간복잡도는 최선의 경우 최악의 경우 모두 O(n^2)
버블 정렬

앞에서부터 둘씩 비교해서 큰 애를 뒤로 보낸다. 한 바퀴 돌 때마다 가장 큰 애가 맨 뒤로 가게 된다. 시간복잡도는 최선의 경우 최악의 경우 모두 O(n^2)
버블 정렬 같은경우엔 최선의 경우를 O(n)까지 줄이도록 개선하는 방법이 있다. 한바퀴돌았는데 스왑이 한번도 일어나지 않으면 탈출하는 것. 한바퀴(n)돌았는데 다 정렬되어 있는 상태라면 거기서 탈출이 가능할 것이다.
Repeat until no swaps
For i from 0 to n–2
If i'th and i+1'th elements out of order
Swap them삽입 정렬
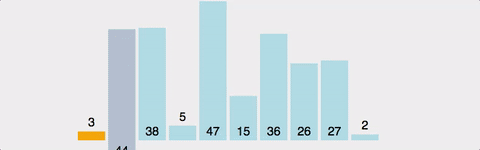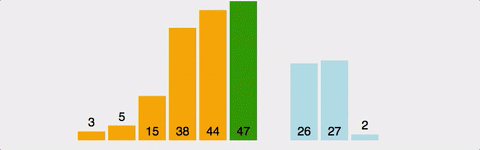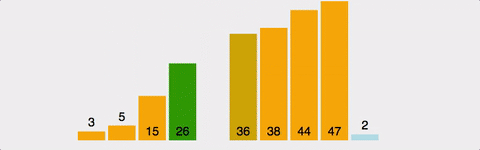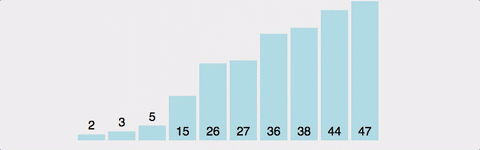
i번째 원소를 골랐을때...i-1부터 0까지 보면서 적절한 위치에 삽입한다. i-1까지는 정렬되어 있는 상태이므로, 상황에 따라 비교를 적게 할 수도 있다. 최선의 경우 (이미 정렬된 경우) 시간복잡도 O(n). 최악의 경우(역순정렬된 경우) 시간복잡도 O(n^2)
병합 정렬

분할 정복 방식으로 설계된 정렬 방식. 시간복잡도 O(nlogn)
퀵정렬
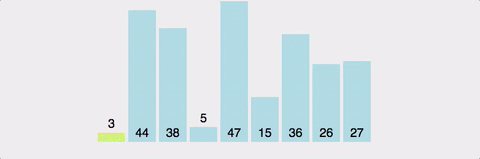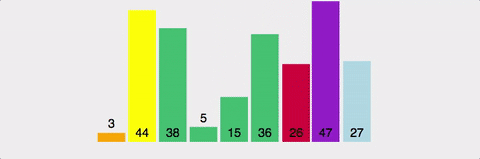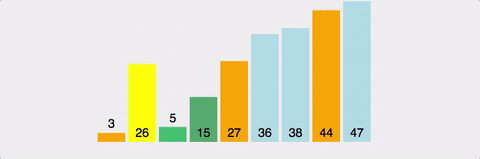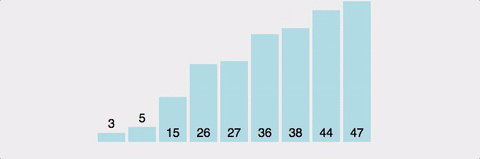
마찬가지로 분할 정복 방식. pivot이라는 값을 설정하고, 이값보다 크면 오른쪽으로, 작으면 왼쪽으로 보낸다.

피벗 설정을 어떻게 하느냐에 따라 성능이 다르다.
최악의 경우(이미 정렬된 경우) 시간복잡도 O(n^2)
평균적, 최선 시간복잡도 O(nlogn)
BigO란 무엇인지 설명
BigO란 알고리즘의 시간복잡도를 나타내는 표기법입니다.
DFS와 BFS의 차이
dfs와 bfs 모두 그래프를 탐색하는 방법입니다. dfs는 현재 정점에서 갈 수 있는 점들까지 들어가면서 탐색하고, bfs는 현재 정점에 연결된 가까운 점들부터 탐색합니다.
bfs는 큐로 구현하고, dfs는 재귀함수 또는 스택으로 구현한다.

알고리즘 문제풀 때 그래프 문제인지는 알겠는데 bfs로 풀어야 하는지 dfs로 풀어야 하는지 헷갈릴 때가 많았다. 아래는 이를 구분할 수 있는 몇가지 특징들이다.
- 검색 대상이 크다면 DFS, 크지 않으면 BFS
- 최단거리 구하는 문제는 BFS가 유리
- 경로의 특징(가중치 등..) 저장해야 하는 문제는 DFS가 유리
그래프(Graph)와 트리(Tree)의 차이점
그래프는 연결되어 있는 객체간의 관계를 표현할 수 있는 자료구조입니다. 트리는 그래프의 일종입니다. 트리는 루트 노드를 가지며, 부모-자식 관계로 이루어져있고, 사이클을 가져선 안됩니다.
트리의 순회는 전위순회, 중위 순회, 후위 순회로 이루어진다. 얘네들은 dfs,bfs에 포함된다.
- 전위 순회는 현재 노드를 방문 후 왼쪽 서브 트리, 오른쪽 서브 트리 순으로 전위 순회를 한다.
- 중위 순회는 왼쪽 서브 트리를 중위 순회한 후 현재 노드를 방문하고, 마지막으로 오른쪽 서브 트리를 중위 순회한다.
- 후위 순회는 왼쪽 서브 트리, 오른쪽 서브 트리 순으로 후위 순회한 후, 마지막으로 현재 노드를 방문한다.

각각의 순환 결과는 다음과 같다. - 전위 순회 : 1 2 4 5 3
- 중위 순회 : 4 2 5 1 3
- 후위 순회 : 4 5 2 3 1
(문제 출처: 카카오 2018 필기시험)
Stack와 Queue의 차이점
스택은 후입선출(LIFO)로 마지막에 넣은 데이터가 가장 먼저 나오고, 큐는 선입선출(FIFO)로 먼저 넣은 데이터가 먼저 나갑니다.
HashTable의 개념, HashMap과 HashTable의 차이점
HashMap과 Hashtable은 데이터를 키와 값으로 관리하는 자료구조입니다. HashTable은 동기화를 지원하고, HashMap은 동기화를 지원하지 않습니다.
HashTable이 동기화를 지원해 Thread-safe 하므로 멀티스레드 환경에서는 HashTable을 써야한다. 멀티스레드가 아니라면 HashMap이 성능이 더 좋으니까 HashMap 쓰는게 좋다.
Fibonacci에서 세가지 (Recursion, Dynamic Programming, 반복) 방식에 대한 시간복잡도와 공간복잡도 차이
재귀로 구현할 경우 시간복잡도는 O(2^n)입니다. 동적계획법과 반복으로 구현할 경우 시간복잡도는 O(n)입니다.
재귀
def fibo(n):
return fibo(n-1) + fibo(n-2) if n >= 2 else n
for n in range(1, 11):
print(n, fibo(n))시간복잡도:O(2^n)
공간복잡도:O(2^n)
반복
def fibo(n):
if n < 2:
return n
a, b = 0, 1
for i in range(n-1):
a, b = b, a + b
return b
for n in range(1, 11):
print(n, fibo(n))시간복잡도:O(n)
공간복잡도:O(n)
dp
if dp[k]!=-1:
return dp[k]
elif k==0:
return 0
elif k==1:
return 1
else:
dp[k]=Fibo(k-1)+Fibo(k-2)
시간복잡도:O(n)
공간복잡도:O(n)
Array와 LinkedList의 차이가 무엇인가?
array는 요소들을 인덱스를 통해 직접 접근할 수 있으므로 O(1) 시간만에 접근할 수 있습니다. LinkedList는 순차적으로 찾아야 하므로 특정 요소를 검색할 때 O(n)의 시간이 걸립니다.

요소 접근
배열: O(1)
연결리스트: O(n)
삽입,삭제
배열: O(n)
연결리스트: O(1)
크기
배열: 크기 고정
연결리스트: 크기 동적
삽입과 삭제가 번번히 이루어진다면, 연결리스트 사용이 좋음.
이미 만들어진 구조에서 데이터의 접근만 필요하면 배열이 좋음.
Priority Queue의 동작 원리는?
우선순위 큐는 우선순위가 먼저 나오는 자료구조입니다. 루트 노드에 우선순위가 높은 데이터를 위치시키는 자료구조인 힙을 이용하여 우선순위 큐를 구현합니다.
🔎 Heap이란?
- 힙은 Complete Binary Tree(완전 이진 트리=마지막을 제외한 모든 노드의 자식들이 꽉 채워진 이진 트리
- 모든 노드에 저장된 값(우선순위)들은 자식 노드들의 것보다 (우선순위가) 크거나 같다.

예를 들어 위 그림은 루트에 젤 큰값이 오는 최대힙이다.
루트가 제일 큰 건 알겠는데 왼쪽 자식, 오른쪽 자식 배치는 조금 의문스러운데...그 이유는 일단 삽입할때 트리 끝에 냅다 위치시킨 다음 한칸 한칸 올라가며 자신의 자리를 찾기 때문이다.
Heap에서 insert, remove 할 시에 각각 시간복잡도
Heap에서 insert, remove 할 시 시간복잡도는 O(logn)입니다.
🔎 재구조화(heapify)
삽입과 삭제 시 다시 최대 힙의 조건을 만족하도록 노드의 위치를 바꾸는 것을 재구조화(heapify)라고 한다. 힙에서 삽입,삭제 자체는 O(1) 시간이 걸리지만 이 재구조화에 O(logn) 시간이 걸린다.
