
회사에서 프로그래머스 문제풀이 스터디를 시작하였다!
매주 각자 문제를 풀어가고, 좀 인상깊었던 문제는 각자의 풀이 방법을 공유하는 방식으로 하는데~~~
이번주는 코딩테스트 입문 day1~2까지 풀기 였고, 나머지는 다 사칙연산 관련 문제였는데 분수의 덧셈 문제가 푸는데 살짝 시간이 걸렸다.
문제
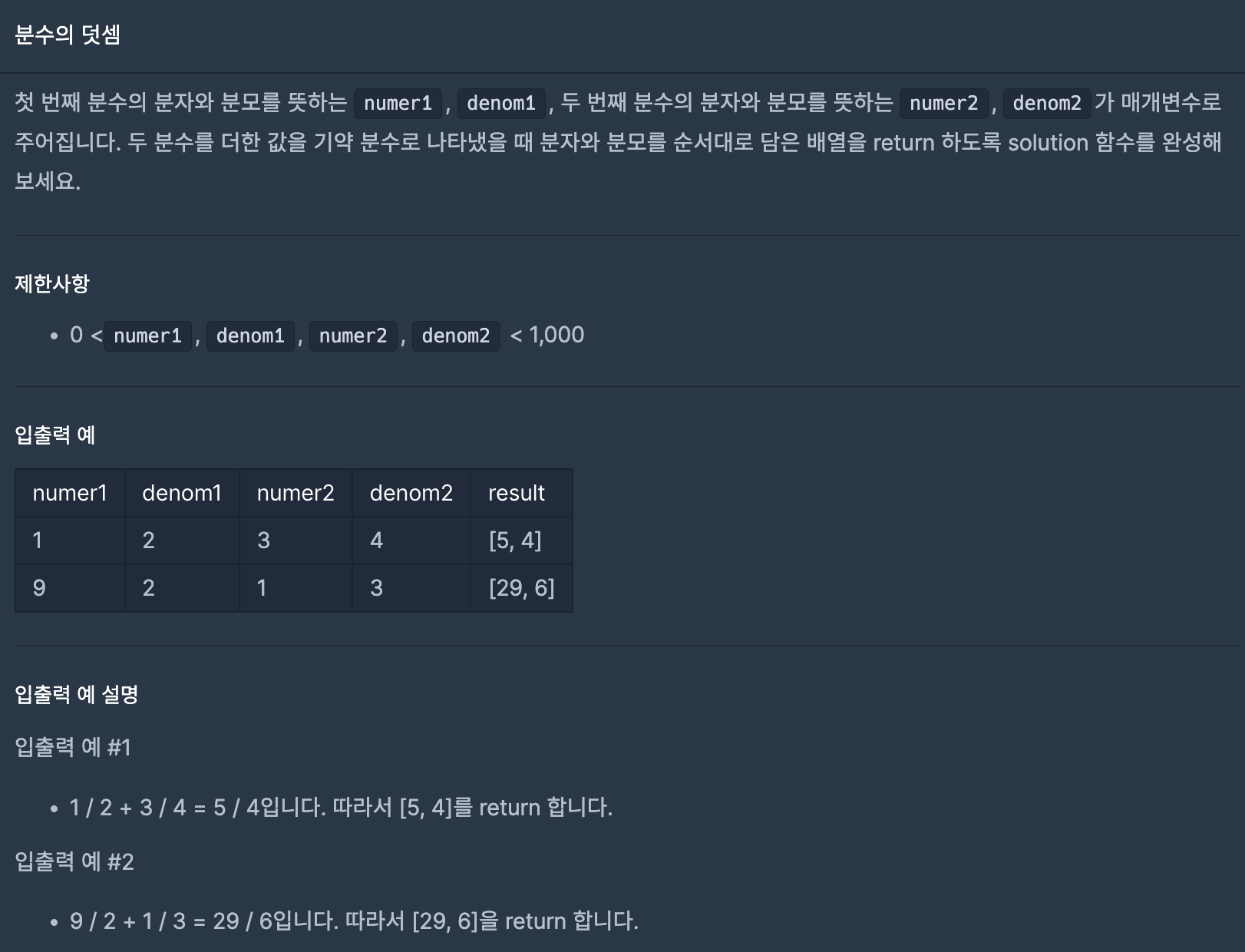
문제는 간단했다. 두 분수의 덧셈을 기약분수로 나타내면 되는 것.
생각한 방식
우선 두 가지 단계가 필수적이었다.
- 분수를 더하기
- 기약분수로 나타내기
1. 분수를 더하기
- 분수를 더하는 것은 간단했다.
- 두 개의 분수를 더하기 위해서는 분모를 통일시키고, 각각의 분모에 곱한 값을 분자에도 똑같이 곱해준 뒤에 분자끼리 더해주면 된다.
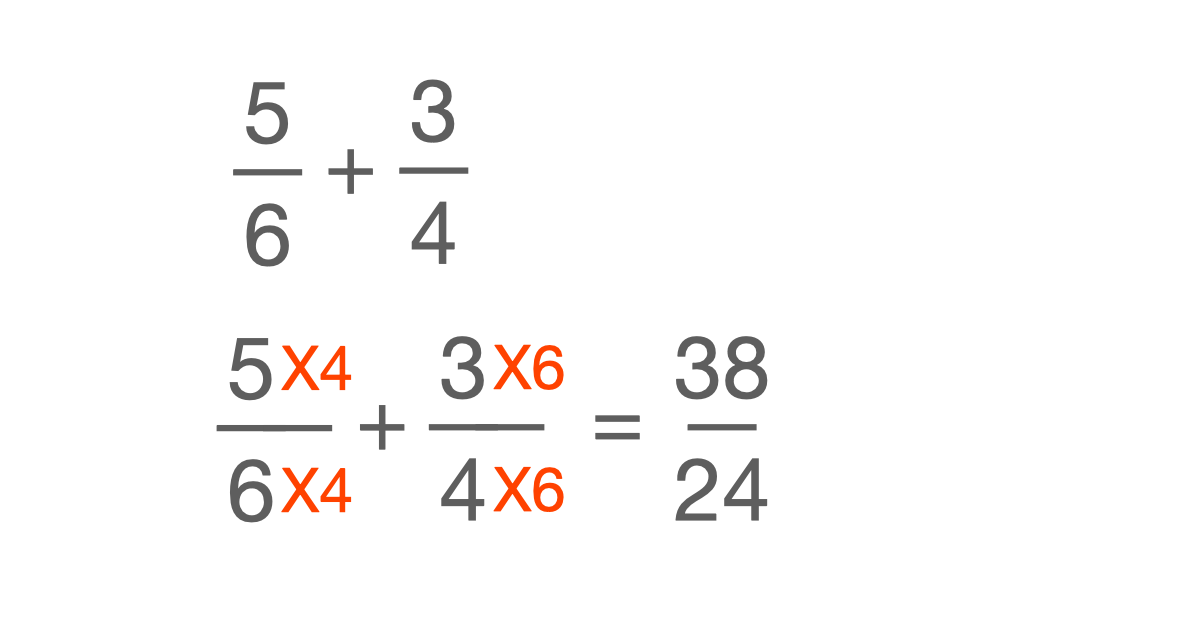
function solution(numer1, denom1, numer2, denom2) {
var answer = [];
// 분수를 더하기
let newNumer = numer1 * denom2 + numer2 * denom1;
let newDenom = denom1 * denom2;
}
하지만, 문제의 조건이 기약분수로 나타내는 것이고..
어렸을 때에도 기약분수로 만들어서 최종 제출하는 것이 원칙이었던 기억..
그러기 위해서는 분자, 분모가 더이상 약분이 되지 않는 형태로 나누어 져야 하는데
=== 분모, 분자를 최대공약수로 나누자
2. 최대공약수 구하는 방법
2-1. for문을 사용하기 (비추천 방식)
- 최대공약수를 함수로 구하는 방법... 을 생각하다가 for문을 이용하기로 했다.
- 그래도 그나마 연산 횟수를 줄이기 위하여 분모, 분자 중 더 작은 수를 알아내고,
- 그 수(더 작은 수)에 도달할 때 까지, 분모, 분자 모두 i로 나누었을 때의 나머지가 0인 i의 값을 구하고,
- 최종으로 구해진 i가 최대공약수다 라고 계산을 하였다.
function solution(numer1, denom1, numer2, denom2) {
var answer = [];
// 분수를 더하기
let newNumer = numer1 * denom2 + numer2 * denom1;
let newDenom = denom1 * denom2;
// 최대공약수를 구하기
let yaksu = 0;
// 분모와 분자 중 더 작은 수 구하기
const smaller = (newNumer < newDenom) ? newNumer : newDenom ;
for (i = 0; i <= smaller; i++) {
if (newNumer % i === 0 && newDenom % i === 0) {
yaksu = i;
}
}
// 분모, 분자를 최대공약수로 나누어주기
answer = [newNumer / yaksu, newDenom / yaksu];
return answer;
}왜 비추천을 하나요?
우선 for문을 사용한다는 것은 n의 개수에 따라 계산 횟수가 늘어나게 된다.
분모나 분자가 4자리수면,, 백만번 넘는 포문을 돌 수도..
2-2. 유클리드 호제법을 사용하기 (추천)
- 다른 분이 푼 방식이 뭔가 놀라워서 공유를 해보자면..!
유클리드 호제법을 사용하는 것이다.
유클리드 호제법이 뭔데?
이름을 들으면 엥? 할 수도 있는데 사실 우리가 어렸을 때 배운 최대 공약수, 최소 공배수를 구하는 방식이 유클리드 호제법이다.
보통은 첨부된 캡처화면의 1번 방식을 사용해서 구해왔는데,
2번의 방식을 참고하여 이번 문제에 적용시킬 수 있다.
출처 : https://www.youtube.com/watch?v=R1gxRwXRpMQ
-
1번에 더하는 방식까지는 같지만, 유클리드 호제법을 사용하여 최대공약수를 구하는 getGcd라는 함수를 따로 구현하였다.
-
num1과 num2를 인자로 받았을 때, num1을 num2로 나눈 나머지가 0이면 num2를 반환하고, 그렇지 않으면 다시 그 나머지와 num2를 같은 방식으로 계속 계산해 나가는 것이다.
(캡처 그림 참고)
function solution(numer1, denom1, numer2, denom2) {
var answer = [];
let newNumer = numer1 * denom2 + numer2 * denom1;
let newDenom = denom1 * denom2;
const gcd = getGcd(newNumer, newDenom);
answer = [newNumer / gcd, newDenom / gcd];
return answer;
}
const getGcd = (num1, num2) => {
if (num1 % num2 === 0) return num2;
return getGcd(num2, num1 % num2);
};
서로 다른 두 방식의 시간 차이
다른 문제들도 보통 2-5배 차이가 나지만, 특히 1, 8, 9, 10번 같은 경우를 보면 그 시간 차이가 어마어마한 것을 알 수 있다.. 아마 파라미터로 들어오는 수가 엄청나게 큰 수 일 것이다.
(지금 제한사항에 1,000미만이라고 하였는데, 그럼에도 저정도면.. 10,000이 넘어가면???????????? for문을 사용하는 방법은 옳지 않음을 알 수 있음)
-
for문 사용한 방식
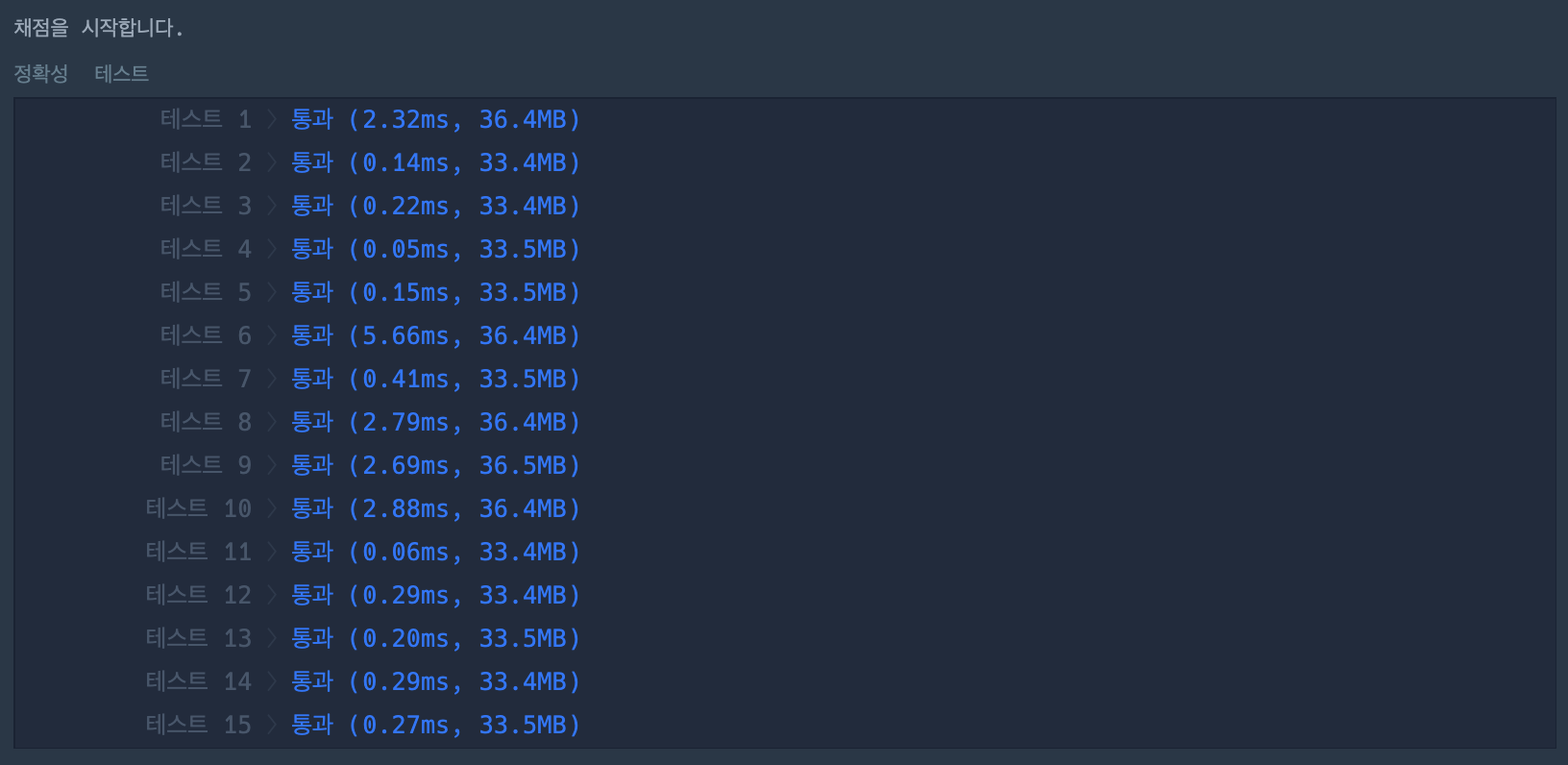
-
유클리드 호제법을 사용한 방식
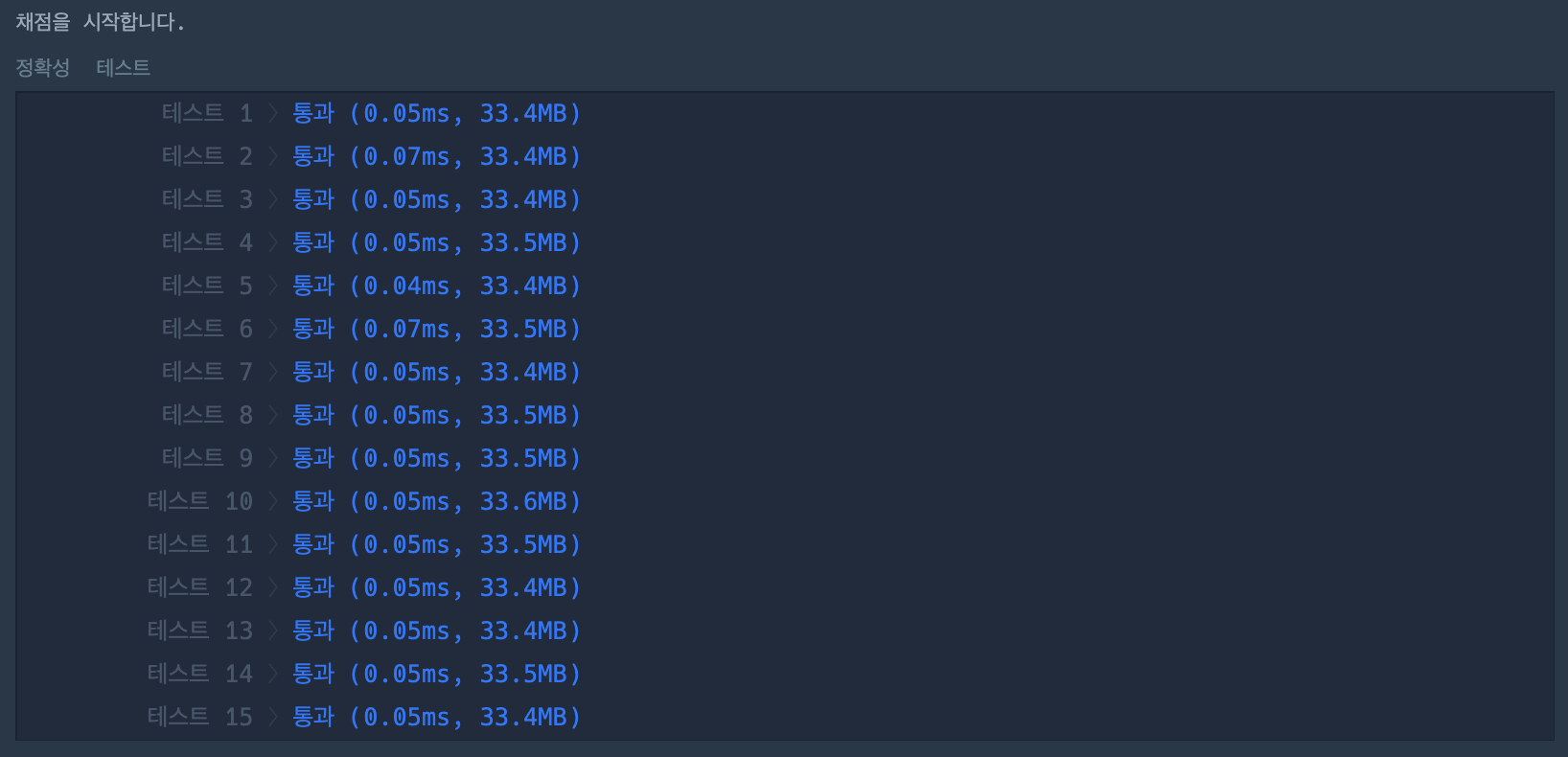
느낀점
- 코딩테스트 문제를 풀다가 이게 수학적으로 생각하면 풀 수 있는데, 코드로 치려고 하니까 어떻게 쳐야할 지 모르겠어서 이중,, 삼중,, 포문을 사용해서 꾸역꾸역 해낸 경우가 많다.
- 우리가 최대공약수를 구할때 1부터 나눠보면서 하지 않는 것처럼 말이다 ^^
- 수학적으로 풀 수 있는 문제는 어떻게든 코드로 구현할 수 있지 않겠냐!!! 라는 것을 깨달음. 지금까지 풀었던 저난이도 문제들을 좀 더 시간 복잡도를 생각하는 방향으로 풀이 방식을 개선해보아야겠다.
