자료 구조 (Data Structure)
자료 구조는 효율적으로 데이터를 관리하고 수정, 탐색, 저장할 수 있는 데이터 집합을 말한다.
추상적 자료형이 정의한 연산들을 구현한 구현체로 ADT를 본격적으로 구현하기 시작하는 단계이다. (책장 속 책을 배열하는 방법)
1. 복잡도
복잡도는 시간 복잡도와 공간 복잡도로 나뉜다.
1-1. 시간 복잡도 (Time Complexity)
- 시간 복잡도는 문제를 해결하는 데 걸리는 시간과 입력의 함수 관계를 말한다.
- 자료 구조의 오퍼레이션 혹은 알고리즘이 얼마나 빠르고 느린지 측정하는 방법인데, ‘실제 시간’을 측정하는 것이 아니라 얼마나 많은 ‘절차 혹은 단계(steps)’로 있는가를 측정한다.
- 시간 복잡도는 효율적인 코드로 개선하는 데 쓰이는 척도가 된다.
1-2. 공간 복잡도 (Space Complexity)
- 공간 복잡도는 프로그램을 실행시켰을 때 필요로 하는 자원 공간의 양을 말한다.
- 정적 변수로 선언된 것 말고도 동적으로 재귀적인 함수로 인해 공간을 계속해서 필요로 할 경우도 포함한다.
2. 빅오 표기법 (Big O Notation)
- 빅오 표기법이란 알고리즘의 성능을 나타내는 표기법으로 시간, 공간 복잡도 예측시 사용한다.
- N값(인풋)의 증가에 따른 처리 시간 또는 필요 공간을 계산한다. 즉, 알고리즘의 직접적인 모든 연산 횟수를 계산하는 것이 아닌 인풋의 증가에 따른 연산 처리 시간의 증가율을 예측하는 척도라고 할 수 있다.
- 표기법: 일반적으로 상수와 계수를 제거하고 알고리즘의 복잡도를 단순화하여 나타냄.
- cf. 계수: 숫자 또는 문자의 곱에서의 숫자 (ex: 2x에서의 계수는 2)
- 표기법: 일반적으로 상수와 계수를 제거하고 알고리즘의 복잡도를 단순화하여 나타냄.
- 빅오 표기법의 장점: 연산 횟수 계산법을 하나의 일관된 형식으로 만들어주며 알고리즘의 런타임이 인풋의 증가에 따라서 어떻게 함께 증가 하는지에 대해 설명 가능해짐.
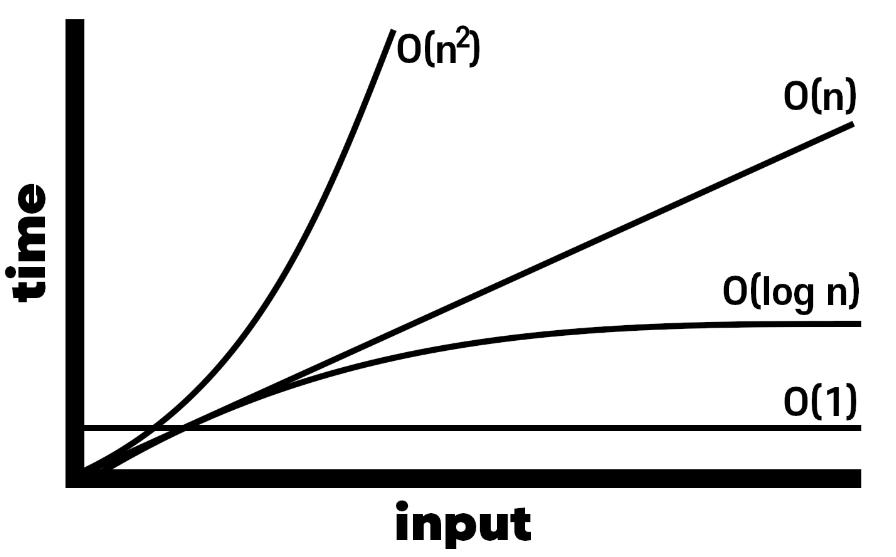
- 시간 복잡도 순서: 0(1) < O(log n) < O(n) < O(n²)
2-1. 상수 시간(Constant Time): O(1)
- 인풋이 늘어나도 변하지 않는다.
const arr = ['a', 'b', 'c', 'd'];
const printFirst = (arr) => {
console.log(arr[0]);
}
printFirst(arr);
// a (Step 1)- 위 예시처럼, arr의 아이템(인풋)이 늘어난다고 해도 출력하는 것은 1번 뿐이므로, 이 함수는 동일한 수의 step이 필요하다. 따라서 해당 경우 인풋에 따라 시간 복잡도는 영향을 받지 않는다. 이 함수의 시간 복잡도는 상수 시간(constant time) = O(1)이다.
- 만약 아래 예제처럼 5번의 Steps을 거친다고 해도 O(5)가 아닌 O(1)이다. BigO는 함수가 인풋 사이즈에 따라 어떻게 작동하는지 큰 원리를 중요시할 뿐, 함수의 디테일을 따지지 않는다. 따라서 상수는 신경쓰지 않는다.
const arr = ['a', 'b', 'c', 'd'];
const printFirst = (arr) => {
console.log(arr[0]); // (Step 1)
console.log(arr[0]); // (Step 2)
console.log(arr[0]); // (Step 3)
console.log(arr[0]); // (Step 4)
console.log(arr[0]); // (Step 5)
} - 이처럼 인풋 사이즈에 관계없이 Step이 정해진 알고리즘들의 시간 복잡도는 O(1)이다.
2-2. 로그 시간(Logarithmic Time): O(log n)
- 예시) 이진 검색 알고리즘(이진 검색에서는 각 프로세스의 스텝을 절반으로 나눠 진행)
- 로그 예제) 로그의 예제는 아래와 같다. 하지만 BigO는 특성상, 밑(base) 숫자는 제거한다.
n = log₂32
32 / 2 = 16 (1번)
16 / 2 = 8 (2번)
8 / 2 = 4 (3번)
4 / 2 = 2 (4번)
2 / 2 = 1 (5번)
따라서, n = 5
(2를 밑(base)으로 하는 32의 로그는 5)
하지만, BigO는 특성상 밑(base)의 숫자를 제거한다.
n = log322-3. 선형 시간(Linear Time): O(n)
- 예제) 아래 예제의 arr의 길이는 5이며, for() 반복문을 통해 5번에 거쳐 요소들을 하나씩 출력하므로 5개의 Steps로 동작할 것이다. 배열이 커지면(인풋 사이즈가 커지면) 필요 스텝도 커진다. 따라서 해당 시간 복잡도는 O(n)이다.
const arr = ['a', 'b', 'c', 'd', 'e'];
const printAll = (arr) => {
for (let n of arr) console.log(n);
}
printAll(arr);
// a (Step 1)
// b (Step 2)
// c (Step 3)
// d (Step 4)
// e (Step 5)- 만약 위 예제를 다음과 같이 해당 함수 내에서 for() 반복문을 두 번 반복한다고 해도, BigO는 상수의 디테일은 무시하기에 O(2n)이 아닌 O(n)이다.
const arr = ['a', 'b', 'c', 'd', 'e'];
const printAll = (arr) => {
for (let n of arr) console.log(n);
for (let n of arr) console.log(n);
}2-4. 지수 시간(Exponent Time) / 2차 시간(Quadratic Time): O(n²)
- 예제) 중첩 반복(Nested Loops)이 있을 때 발생. 루프 안의 루프에서 함수를 실행하므로 시간 복잡도는 인풋의 n^2이다.
const printTwice = (arr) => {
for i of arr {
for j of arr {
console.log(i, j)
}
}
}3. 자료 구조에서의 시간 복잡도
3-1. 자바스크립트 함수들의 시간 복잡도
| method name | Big(o) |
|---|---|
| push() | O(1) |
| pop() | O(1) |
| shift() | O(n) |
| unshift() | O(n) |
| splice() | O(n) |
| sort() | O(n log n) |
| concat() | O(n) |
| slice() | O(n) |
| indexOf() | O(n) |
| map() | O(n) |
| filter() | O(n) |
| reduce() | O(n) |
3-2. 자료 구조에서의 시간 복잡도
▼ 평균 시간 복잡도
| 자료 구조 | 접근 | 탐색 | 삽입 | 삭제 |
|---|---|---|---|---|
| 배열 | O(1) | O(n) | O(n) | O(n) |
| 스택 | O(n) | O(n) | O(1) | O(1) |
| 큐 | O(n) | O(n) | O(1) | O(1) |
| 이중 연결 리스트 | O(n) | O(n) | O(1) | O(1) |
| 해시 테이블 | O(1) | O(1) | O(1) | O(1) |
| 이진 탐색 트리 | O(log n) | O(log n) | O(log n) | O(log n) |
| AVL 트리 | O(log n) | O(log n) | O(log n) | O(log n) |
| 레드 블랙 트리 | O(log n) | O(log n) | O(log n) | O(log n) |
▼ 최악의 시간 복잡도
| 자료 구조 | 접근 | 탐색 | 삽입 | 삭제 |
|---|---|---|---|---|
| 배열 | O(1) | O(n) | O(n) | O(n) |
| 스택 | O(n) | O(n) | O(1) | O(1) |
| 큐 | O(n) | O(n) | O(1) | O(1) |
| 이중 연결 리스트 | O(n) | O(n) | O(1) | O(1) |
| 해시 테이블 | O(n) | O(n) | O(n) | O(n) |
| 이진 탐색 트리 | O(n) | O(n) | O(n) | O(n) |
| AVL 트리 | O(log n) | O(log n) | O(log n) | O(log n) |
| 레드 블랙 트리 | O(log n) | O(log n) | O(log n) | O(log n) |
Reference.

