[알고리즘] 24일차 (이분 그래프 판별하기) #백준1707번

📌 문제 048) 이분 그래프 판별하기

시간 제한 2초, 골드 IV, 백준 1707번

그래프의 정점의 집합을 둘로 분할하여, 각 집합에 속한 정점끼리는 서로 인접하지 않도록 분할할 수 있을 때, 그러한 그래프를 특별히 이분 그래프 (Bipartite Graph) 라 부른다.
그래프가 입력으로 주어졌을 때, 이 그래프가 이분 그래프인지 아닌지 판별하는 프로그램을 작성하시오.

입력

입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에 두고 순서대로 주어진다. 각 정점에는 1부터 V까지 차례로 번호가 붙어 있다. 이어서 둘째 줄부터 E개의 줄에 걸쳐 간선에 대한 정보가 주어지는데, 각 줄에 인접한 두 정점의 번호 u, v (u ≠ v)가 빈 칸을 사이에 두고 주어진다.

2 # 테스트 케이스 개수
3 2 # 노드 개수, 에지 개수
1 3 # 에지 개수에 맞춰 2줄 입력
2 3
4 4 # 노드 개수, 에지 개수
1 2 # 에지 개수에 맞춰 4줄 입력
2 3
3 4
4 2

출력

K개의 줄에 걸쳐 입력으로 주어진 그래프가 이분 그래프이면 YES, 아니면 NO를 순서대로 출력한다.

YES
NO

1단계 문제 분석

• 노드의 집합을 2개로 나누는데, 인접한 노드끼리 같은 집합이 되지 않도록 적절하게 임의로 분발할 수 있다.
• 트리의 경우에는 항상 이분 그래프가 된다.
• 사이클이 발생하지 않으면 탐색을 하면서 다음 노드를 이번 노드와 다른 집합으로 지정하면 되기 때문이다.
• 단, 사이클이 발생했을 때는 이런 이분 그래프가 불가능할 때가 있다.
  
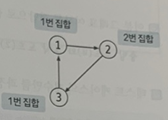
• 기존의 탐색 메커니즘에서 탐색한 노드에 다시 접근하게 됐을 때, 현재 노드의 집합과 같으면 이분 그래프가 불가능하다는 것으로 판별할 수 있다.

1. 입력된 그래프 데이터를 인접 리스트로 구현한다.
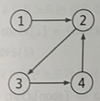
   1 -> 2
   2 -> 3
   3 -> 4
   4 -> 2

2. 모든 노드로 각각 DFS 탐색 알고리즘을 적용해 탐색을 수행한다. DFS를 실행할 때 현재 노드에서 연결된 노드 중 이미 방문한 노드가 나와 같은 집합이면 이분 그래프가 아닌 것으로 판별한다. 실행 결과가 이분 그래프가 아니면 이후 노드를 탐색하지 않는다.

• 1번 노드 DFS 실행
  1 -> 2 -> 3 -> 4 -> "2"
  A -> B -> A -> B -> "B"
• 이미 방문했던 노드 2에 도착함

3. 이분 그래프 여부를 정답으로 출력한다.

• 출발 노드(4)와 도착 노드(2)의 집합이 같으므로 이분 그래프가 불가능하다. -> NO 출력

4. 테스트 케이스의 개수만큼 1~3번을 반복한다.

• 여기서 모든 노드로 DFS를 실행하는 이유는 그래프의 모든 노드가 이어져 있지 않고, 여러 개의 부분 그래프로 이뤄진 케이스가 존재할 수 있기 때문이다.

2단계 슈도 코드

N(테스트 케이스 개수)
IsEven(이분그래프 판별 변수)

# DFS 구현하기
DFS:
    visited 리스트에 현재 노드 방문 기록하기
    if 현재 노드의 연결 노드 중 방문하지 않은 노드:
    	현재 노드와 다른 집합으로 연결 노드 집합 저장
        DFS(다음 노드)
    elif 이미 방문한 노드인데, 현재 나의 노드와 같은 집합:
    	이분 그래프가 아님

for N만큼 반복:
	V(노드 개수)
    E(에지 개수)
    A(그래프 데이터 저장 인접 리스트)
    visited(방문 기록 저장 리스트)
    check(노드별 집합 저장 리스트)
    IsEven = True # 이분 그래프 판별 변수 초기화
    
    for E만큼 반복:
    	A 인접 리스트에 그래프 데이터 저장하기
    
    for V만큼 반복:
    	각 노드에서 DFS 실행 -> 결과가 이분 그래프가 아니면 반복 종료
    
    이분 그래프 여부 출력

3단계 코드 구현

import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
N = int(input())
IsEven = True

def DFS(node): # DFS 탐색 함수 구현
    global IsEven
    visited[node] = True
    for i in A[node]:
        if not visited[i]:
            # 인접 노드는 같은 집합이 아니므로 다른 집합으로 처리
            check[i] = (check[node]+1)%2
            DFS(i)
        # 이미 방문한 노드가 현재 내 노드와 같은 집합이면 이분 그래프 아님
        elif check[node] == check[i]:
            IsEven = False


for _ in range(N):
    V, E = map(int, input().split())
    A = [[] for _ in range(V + 1)]
    visited = [False] * (V + 1)
    check = [0] * (V + 1)
    IsEven = True
    
    for i in range(E): # 인접 리스트로 그래프 저장
        Start, End = map(int, input().split())
        A[Start].append(End)
        A[End].append(Start)
    
    # 주어진 그래프가 항상 1개가 아니므로 모든 노드에서 수행
    for i in range(1, V + 1):
        if IsEven:
            DFS(i)
        else:
            break
    
    if IsEven:
        print("YES")
    else:
        print("NO")