자료구조
03-1 배열과 리스트
🔎 배열
• 인덱스를 사용하여 값에 바로 접근할 수 있다.
• 새로운 값을 삽입하거나 특정 인덱스에 있는 값을 삭제하기 어렵다. 값을 삽입하거나 삭제하려면 해당 인덱스 주변에 있는 값을 이동시키는 과정이 필요하다.
• 배열의 크기는 선언할 때 지정할 수 있으며, 한 번 선언하면 크기를 늘리거나 줄일 수 없다.
• 구조가 간단하므로 코딩 테스트에서 많이 사용한다.
🔎 리스트
값과 포인터를 묶은 노드(값, 포인터를 쌍으로 갖는 기초 단위)라는 것을 포인터로 연결한 자료구조
• 인덱스가 없으므로 값에 접근하려면 Head 포인터부터 순서대로 접근해야 한다. 다시 말해 값에 접근하는 속도가 느리다.
• 포인터로 연결되어 있으므로 데이터를 삽입하거나 삭제하는 연산 속도가 빠르다.
• 선언할 때 크기를 별도로 지정하지 않아도 된다. 다시 말해 리스트의 크기는 정해져 있지 않으며, 크기가 변하기 쉬운 데이터를 다룰 때 적절하다.
• 포인터를 저장할 공간이 필요하므로 배열보다 구조가 복잡하다.
파이썬은 배열과 리스트를 구분하지 않고 리스트(list)가 배열과 리스트의 특징 모두 가지도록 구현되어 있으므로, 이러한 특징을 잘 활용하면 다른 언어보다 조금 더 쉽게 정답 코드를 구현할 수 있다.
📌 문제 001) 숫자의 합 구하기
시간 제한 1초, 브론즈 IV, 백준 11720번
N개의 숫자가 공백 없이 써 있다. 이 숫자를 모두 합해 출력하는 프로그램을 작성하시오.
입력
1번째 줄에 숫자의 개수 N(1<=N<=100), 2번째 줄에 숫자 N개가 공백 없이 주어진다.
11 10987654321
출력
입력으로 주어진 숫자 N개의 합을 출력한다.
46
1단계 문제 분석
• 주어진 숫자를 리스트 형태로 저장한다.
• 해당 리스트를 index를 이용해 탐색하며 각 자릿수의 값을 더한다.
• 자릿수를 더할 때는 정수형으로 변환해 더한다.
2단계 슈도 코드
n값 받기
numbers 변수에 list 함수를 이용하여 숫자를 한 자리씩 나누어 받기
sum 변수 선언
for numbers 탐색:
sum 변수에 numbers에 있는 각 자릿수를 가져와 더하기
sum 출력3단계 코드 구현
n = input()
numbers = list(input())
sum = 0
for i in numbers:
sum = sum + int(i) # numbers에 있는 각 자리 수를 가져와 더하기
print(sum)참고: bool 형 변환은 int/float 변환 시 데이터가 0인지 아닌지에 따라 True/False 반환, chr와 str에서 변환할 때는 값이 비어 있는지 아닌지에 따라 True/False를 반환한다.
📌 문제 002) 평균 구하기
시간 제한 2초, 브론즈 I, 백준 1546번
세준이는 기말고사를 망쳤다. 세준이는 점수를 조작해서 집에 가져가기로 했다. 일단 세준이는 자기 점수 중에 최댓값을 골랐다. 이 값을 M이라고 한다. 그리고 나서 모든 점수를 점수 / M x 100으로 고쳤다.
예를 들어, 세준이의 최고점이 70이고, 수학 점수가 50이었으면 수학 점수는 50 / 70 x 100이 되어 71.43점이 된다.
세준이의 성적을 위의 방법대로 새로 계산했을 때, 새로운 평균을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 시험 본 과목의 개수 N이 주어진다. 이 값은 1000보다 작거나 같다. 둘째 줄에 세준이의 현재 성적이 주어진다. 이 값은 100보다 작거나 같은 음이 아닌 정수이고, 적어도 하나의 값은 0보다 크다.
3 40 80 60
출력
첫째 줄에 새로운 평균을 출력한다. 실제 정답과 출력값의 절대오차 또는 상대오차가 10^(-2) 이하이면 정답이다.
75.0
1단계 문제 분석
최고 점수를 기준으로 다시 계산해야 하기 때문에 모든 점수 입력받은 후 최고점은 별도로 저장해야 한다. 또한 문제에서 제시한 점수 계산 식은 총합과 관련된 식으로 변환 가능하다. 따라서 일일이 변환 점수를 구할 필요 없이 한 번에 변환한 점수의 평균 점수를 구할 수 있다.
( A / M x 100 + B / M x 100 + C / M x 100 ) / 3 = ( A + B + C ) x 100 / M / 3
2단계 슈도 코드
n에 과목의 수 입력
mylist에 점수 정보 저장
mymax에 mylist 정보 중 최댓값 저장
sum에 mylist 모든 데이터 값 더하기
sum * 100 / mymax / n 출력3단계 코드 구현
n = input()
mylist = list(map(int, input().split()))
mymax = max(mylist)
sum = sum(mylist)
print(sum * 100 / mymax / int(n))03-2 구간 합
🔎 구간 합 핵심 이론
구간 합 알고리즘을 활용하려면 먼저 합 배열을 구해야 한다.
합 배열 S 정의
S[i] = A[0] + A[1] + A[2] + ... + A[i-1] + A[i] #A[0]부터 A[i]까지의 합
합 배열은 리스트 데이터를 전처리한 배열이다. 합 배열을 미리 구해 놓으면 기존 리스트의 일정 범위의 합을 구하는 시간 복잡도가 O(N)에서 O(1)로 감소한다.
합 배열 S를 만드는 공식
S[i] = S[i-1] + A[i]
i에서 j까지 구간 합 공식
S[j] - S[i-1]
ex) A[2] ~ A[5] 구간 합
S[5] = A[0] + A[1] + A[2] + A[3] + A[4] + A[5]
S[1] = A[0] + A[1]
S[5] - S[1] = A[2] + A[3] + A[4] + A[5]
📌 문제 003) 구간 합 구하기 1
시간 제한 0.5초, 실버 III, 백준 11659번
수 N개가 주어졌을 때 i번째 수에서 j번째 수까지의 합을 구하는 프로그램을 작성하시오.
입력
1번째 줄에 수의 개수 N(1 <= N <= 100,000), 합을 구해야 하는 횟수 M(1 <= M <= 100,000), 2번째 줄에 N개의 수가 주어진다. 각 수는 1,000보다 작거나 같은 자연수다. 3번째 줄부터는 M개의 줄에 합을 구해야 하는 구간 i와 j가 주어진다.
5 3 # 데이터의 개수, 질의 개수 5 4 3 2 1 # 구간 합을 구할 대상 배열 1 3 2 4 5 5
출력
총 M개의 줄에 입력으로 주어진 i번째 수부터 j번째 수까지 합을 출력한다.
12 9 1
1단계 문제 분석
문제에서 수의 개수와, 합을 구해야 하는 횟수는 최대 100,000이다. 매번 합을 계산하면 0.5초 안에 절대 계산을 못한다. 이럴 때 구간 합 개념을 활용하자.
2단계 슈도 코드
suNo(숫자 개수), quizNo(질의 개수)
numbers 변수에 숫자 데이터 저장
prefix_sum 합 배열 변수 선언
temp 변수 선언
for 저장한 숫자 데이터 차례대로 탐색:
temp에 현재 숫자 데이터 더해 주기
합 배열에 temp값 저장
for 질의 개수만큼 반복:
질의 범위 받기(s~e)
구간 합 출력하기(prefix_sum[e] - prefix_sum[s-1])3단계 코드 구현
import sys
input = sys.stdin.readline
suNo, quizNo = map(int, input().split())
numbers = list(map(int, input().split()))
prefix_sum = [0]
temp = 0
for i in numbers:
temp = temp + i
prefix_sum.append(temp)
for i in range(quizNo):
s, e = map(int, input().split())
print(prefix_sum[e] - prefix_sum[s-1])📌 문제 004) 구간 합 구하기 2
시간 제한 1초, 실버 I, 백준 11660번
N×N개의 수가 N×N 크기의 표에 채워져 있다. (x1, y1)부터 (x2, y2)까지 합을 구하는 프로그램을 작성하시오. (x, y)는 x행 y열을 의미한다.
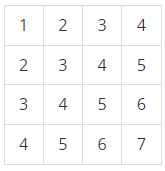
예를 들어, N = 4이고, 표가 아래와 같이 채워져 있는 경우를 살펴보자.
여기서 (2, 2)부터 (3, 4)까지 합을 구하면 3+4+5+4+5+6 = 27이고, (4, 4)부터 (4, 4)까지 합을 구하면 7이다.
표에 채워져 있는 수와 합을 구하는 연산이 주어졌을 때, 이를 처리하는 프로그램을 작성하시오.
입력
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네 개의 정수 x1, y1, x2, y2 가 주어지며, (x1, y1)부터 (x2, y2)의 합을 구해 출력해야 한다. 표에 채워져 있는 수는 1,000보다 작거나 같은 자연수이다. (x1 ≤ x2, y1 ≤ y2)
4 3 # 2차원 배열의 크기, 구간 합 질의의 개수 1 2 3 4 # 원본 배열 1번째 줄 2 3 4 5 # 원본 배열 2번째 줄 3 4 5 6 # 원본 배열 3번째 줄 4 5 6 7 # 원본 배열 4번째 줄 2 2 3 4 # 구간 합 (x1, y1), (x2, y2) 1번째 질의 3 4 3 4 # 구간 합 (x1, y1), (x2, y2) 2번째 질의 1 1 4 4 # 구간 합 (x1, y1), (x2, y2) 3번째 질의
출력
총 M줄에 걸쳐 (x1, y1)부터 (x2, y2)까지 합을 구해 출력한다.
27 6 64
1단계 문제 분석
먼저, 질의의 개수(M)이 100,000이므로 이 문제 역시 매번 합을 구하는 것이 아닌 구간 합 배열을 이용해야 한다. 1차원에서 2차원으로 확장된 것이 핵심이다.
2차원 구간 합 배열 D[X][Y]의 정의
D[X][Y] = 원본 배열의 (0, 0)부터 (X, Y)까지의 사각형 영역 안에 있는 수의 합
D[i][j]의 값을 채우는 구간 합 공식
D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]
질의 x1, y1, x2, y2에 대한 답을 구간 합으로 구하는 방법
D[x2][y2] - D[x1-1][y2] - D[x2][y1-1] + D[x1-1][y1-1]
2단계 슈도 코드
n(리스트 크기), m(질의 수)
A(원본 리스트), D(합 배열)
for n만큼 반복:
원본 리스트 데이터 저장
for i를 1부터 n까지 반복:
for j를 1부터 n까지 반복:
합 배열 저장
D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]
for m만큼 반복:
질의에 대한 결과 계산 및 출력
결과 = D[x2][y2] - D[x1-1][y2] - D[x2][y1-1] + D[x1-1][y1-1]3단계 코드 구현
import sys
input = sys.stdin.readline
n, m = map(int, input().split())
A = [[0] * (n + 1)]
D = [[0] * (n + 1) for _ in range(n + 1)]
for i in range(n):
A_row = [0] + [int(x) for x in input().split()]
A.append(A_row)
for i in range(1, n + 1):
for j in range(1, n + 1):
# 합 배열 구하기
D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]
for _ in range(m):
x1, y1, x2, y2 = map(int, input().split())
# 구간 합 배열로 질의에 답변
result = D[x2][y2] - D[x1-1][y2] - D[x2][y1-1] + D[x1-1][y1-1]
print(result)