Section 1_Sprint 1

Day 1

EDA(Exploratory Data Analysis)

• 데이터 분석에 있어서 매우 중요한 초기 분석 단계
  • 데이터의 특이성 확인
  • 시각화 같은 도구를 통해 패턴 발견
  • 통계화 그래픽을 통해 가설 검정하는 과정 등
• EDA 방법
  • Graphic : 차트 혹은 그림 등을 이용하여 데이터를 확인하는 방법
  • Non-Graphic : 그래픽적인 요소를 사용하지 않는 방법으로 주로 Summary Statistics 를 통해 데이터를 확인하는 방법

Pre-processing

Garbage In Garbage Out

• Cleaning : noise 를 제거하거나 inconsistency 를 보정하는 과정
  -> 데이터를 분석하기 전에 오류를 깨끗이 다듬지 않으면 잘못된 데이터를 통해 잘못된 인사이트, 결론을 얻을 수 있음

• Missing values

  • Ignore the tuple (결측치가 있는 데이터 삭제)
  • Manual Fill (수동으로 입력)
  • Global constant ("Unknown")
  • Imputation (All mean, Class mean, Inference mean, Regression 등)

• Noisy data : 큰 방향성에서 벗어난 random error 혹은 variance 를 포함하는 데이터
  -> 대부분 descriptivestatistics 혹은 visualization 등 (eda)을 통해 제거 가능

• Integration : 여러개로 나누어져 있는 데이터들을 분석하기 편하게 하나로 합치는 과정(ex. merge)

• Transformation : 데이터의 형태를 변화하는 작업, Scaling 이라고 부르기도 함(ex. normalize)

• Reduction : 데이터를 의미있게 줄이는 것을 의미, Dimension reduction과 유사한 목적을 가짐(ex. pca)

Day 2

Feature Engineering

Feature Engineering 은 도메인 지식과 창의성을 바탕으로, 데이터셋에 존재하는 Feature들을 재조합하여 새로운 Feature를 만드는 것

• 목적 : 더 좋은 퍼포먼스를 위하여 더 새롭고, 더 의미있는 패턴을 제공하는 것

🔥 Na, Null, NaN, 0, Undefined 의 차이

• NaN(Not a Number) : 프로그램 상 float 으로 인식, 잘못된 수식으로 인해 발행된 값
• Null : 비어있는 값
• Na(Not available) : 결측치, 사용할 수 없는 값
• Undefined : 비어있는 값, 아직 정의되지 않은 값, False

Day 3

Data manipulation

concat(concatenate)

pd.concat([x,y]) # concat_by_row

pd.concat([x,y], axis = 1) #concat_by_column

데이터 프레임을 더할 때, 일반적으로 더해지는 행, 열의 이름이나 인덱스 값이 일치해야 함
만약 그렇지 않으면 비어있는 부분에 대해서는 (결측치를 의미하는) NaN 값으로 채워짐

Merge

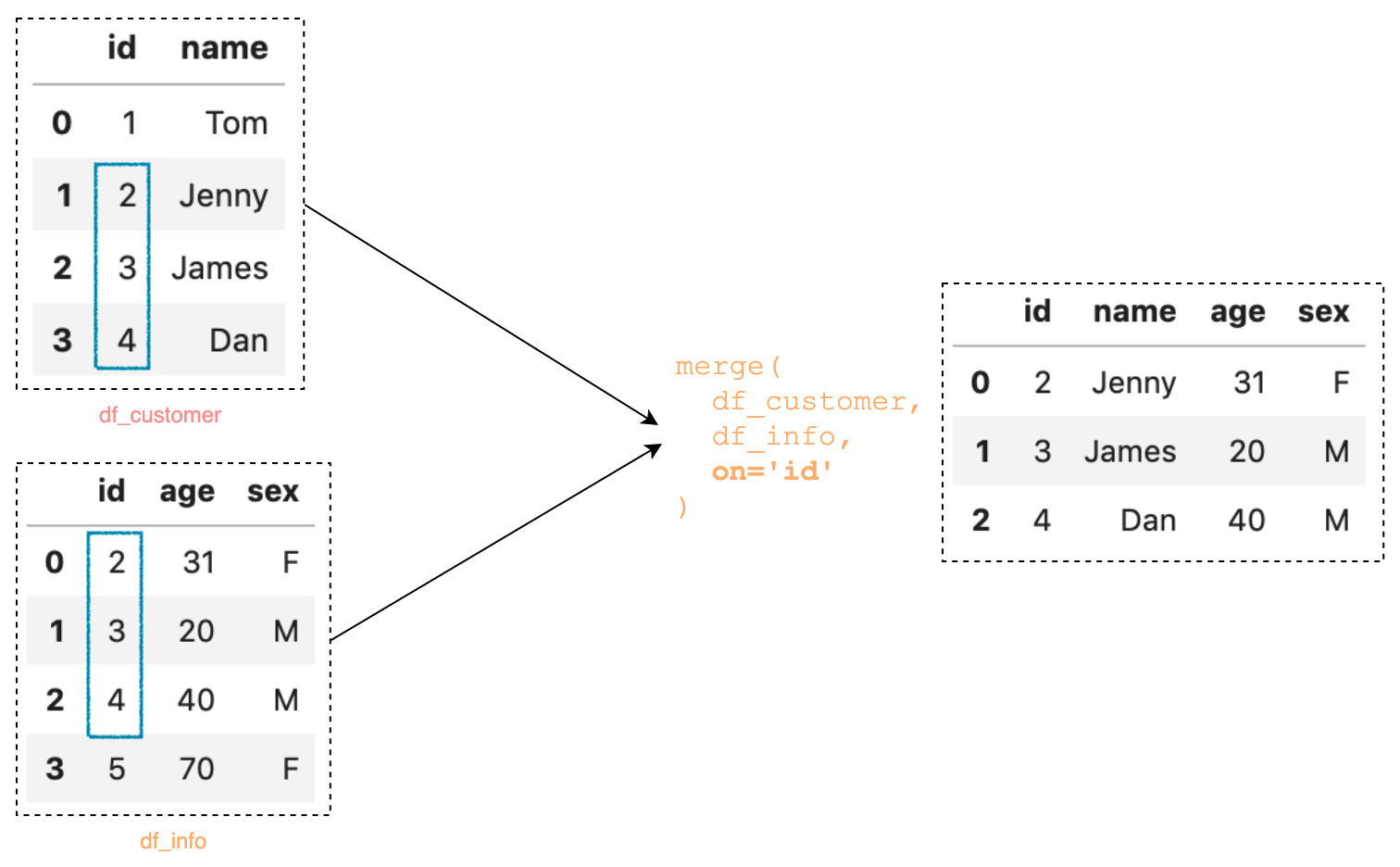
merge는 concat과 다르게 공통된 부분을 기반으로 합치기가 주요 용도

Tidy data

• wide data -> tidy data : melt

• tidy data -> wide data : pivot_table

Day 4

Basic derivative

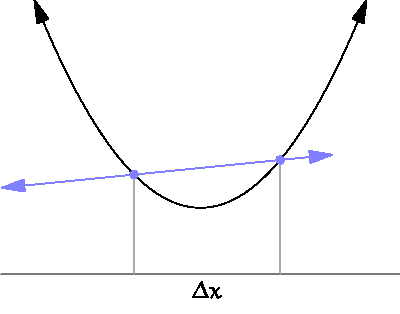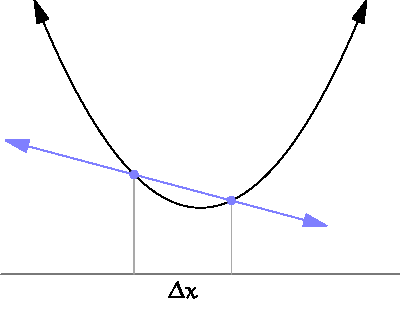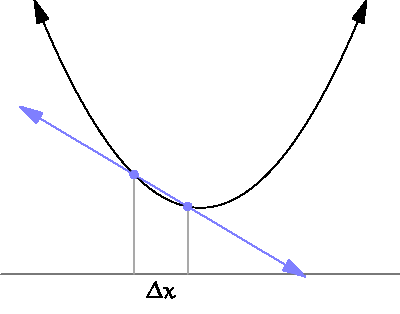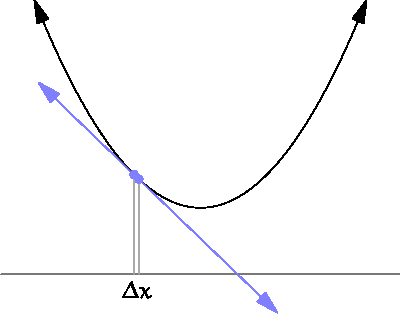미분 : x의 변화량이 한없이 0에 가까워질 때의 기울기 계산하는 것

x를 넣었을 때, y 값을 예측하는 선형 모델은 $\hat y = a + b X$

• 여기서 $\alpha$는 y-절편 (y-intercept), $\beta$는 기울기 (slope)

모델이 더 정확하게 실제값을 예측하기 위해서는

일단 주어진 데이터 X를 넣었을 떄 모델이 예측하는 예측값과 실제값 간의 차이(Error, ε )를 계산한 다음, 여러 모델 중 Error(모델에서 예측하는 예측값과 실제값 (y)의 차이)가 가장 작은 모델을 선택하는 방법을 통해, 가장 좋은 모델을 선택

• 여기서 이 과정은 f(a,b)=ε 로 표현 될 수 있으며, 오차 함수인 ε 을 최소화 하는 a,b 를 찾는 것이 머신러닝(Linear regression)의 목표

• 선형회귀모델의 경우 오차 함수는 보통 Mean Squared Error를 쓰는데, 오차 함수를 최소화하는 a,b 를 구하기 위해서 미분을 사용

• 미분을 통해서 오차 함수의 도함수( f′(x) )가 0이 되는 부분 (즉 변화율이 0인 부분)을 찾아서 오차 함수가 최소화되는 a,b 을 찾는 것

편미분(Partal Derivative)

머신러닝의 error 함수는 여러개의 파라미터 값을 통해 결정되는데 이때 쓰이는 것이 편미분

파라미터가 2개 이상인 Error 함수에서 우선 1개의 파라미터에 대해서만 미분을 하자 라는 목적으로 다른 변수들을 상수 취급 하는 방법

Chain Rule

함수의 함수를 미분하기 위해 사용하는 방식, 합성함수 라고 부르기도 함

공식 : $F(x) = f(g(x))$, $F'(x)$ $\rightarrow$ $f'((g(x)) \cdot g'(x)$

미분을 할 때 바깥 함수($f(x)$)부터 미분을 한 후에 안에 있는 함수 ($g(x)$)를 미분

경사하강법(Gradient Descent)

오차 함수인 𝜀 을 최소화 하는 𝑎,𝑏 를 찾을 수 있는 최적화 알고리즘 중의 하나

임의의 a, b를 선택한 후 (random initialization)에 기울기 (gradient)를 계산해서 기울기 값이 낮아지는 방향으로 진행

기울기는 항상 손실 함수 값이 가장 크게 증가하는 방향으로 진행, 때문에 경사하강법 알고리즘은 기울기의 반대 방향으로 이동

경사하강법에서 a,b는 다음과 같이 계산 :

$a_{n+1} = a_n - \eta ∇ f(a_n)$

$b_{n+1} = b_n - \eta ∇ f(b_n)$

반복적으로 파라미터 a,b를 업데이트 해가면서 그래디언트($∇ f$)가 0이 될 때까지 이동

이 때 중요한게 바로 학습률 (learning rate, $\eta$)

• 학습률이 너무 낮게 되면 알고리즘이 수렴하기 위해서 반복을 많이 해야되고 이는 결국 수렴에 시간을 상당히 걸리게 함
• 반대로 학습률이 너무 크면 오히려 극소값을 지나쳐 버려서 알고리즘이 수렴을 못하고 계산을 계속 반복하게 될 수도 있기 때문에 학습률을 정할 때는 신중하게 정해야 함