
Day 1
Decision Tree
sklearn.pipeline
- 여러 ML모델을 같은 전처리 프로세스에 연결시킬 수 있음
- 그리드처치(grid search)를 통해 여러 하이퍼파라미터를 쉽게 연결할 수 있음
from sklearn.pipeline import make_pipeline
from category_encoders import OneHotEncoder
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
pipe = make_pipeline(
OneHotEncoder(),
SimpleImputer(),
StandardScaler(),
LogisticRegression(n_jobs=-1)
)
pipe.fit(X_train, y_train)pipe.named_steps 속성을 사용하면 유사 딕셔너리 객체로 파이프라인 내 과정에 접근 가능
결정트리(Decision Tree)
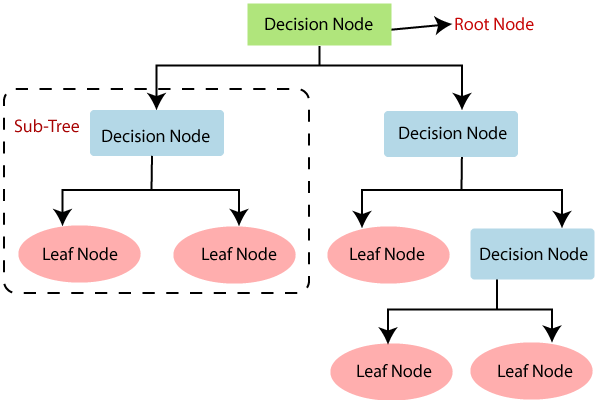
- 결정트리의 각 노드(node)는 뿌리(root)노드, 중간(internal)노드, 말단(external, leaf, terminal) 노드로 나뉨
- 결정트리는 분류와 회귀문제 모두 적용 가능
- 결정트리는 데이터를 분할해 가는 알고리즘
- 새로운 데이터가 특정 말단 노드에 속한다는 정보를 확인한 뒤 말단노드의 빈도가 가장 높은 범주로 데이터를 분류
장점
- 결과 해석 용이 -> 직관적 해석 가능, 주변 변수와 분리기준 제시
- 비모수적 모델 -> 통계모델에 요구되는 가정(정규성, 등분산성, 독립성)에 자유로움
- 변수간 상호작용 -> 변수간 상호작용을 고려하며 선형/비선형 관계 탐색 가능
- Scaling
단점
- 비안정성 -> 과적합으로 정확도 감소
- 선형성 미흡
- 비연속성
결정트리 학습 알고리즘
결정트리를 학습하는 것은 노드를 어떻게 분할하는가에 대한 문제로 결정트리의 비용함수를 정의하고 그것을 최소화 하도록 분할하는 것이 트리모델 학습 알고리즘
- 지니 불순도(Gini Impurity) :
- 엔트로피(Entropy) :
- 불순도(Impurity) : 여러 범주가 섞여 있는 정도
- 불순도 감소 최대, 정보획득 가장 큰 지점 찾아내야 함
- 정보획득(Information gain) : 특정한 특성을 사용하여 분할했을 때 엔트로피의 감소량 = = 분할 전 노드 불순도 - 분할 후 자식노드들의 불순도
과적합 해결
- min_samples_split
- min_samples_leaf : 말단 노드에 최소한 존재해야 하는 샘플들의 수 지정
- max_depth
특성 중요도(Feature importance)
선형모델에서는 특성과 타겟의 관계를 파악하기 위해 회귀 계수를 사용, 트리모델에서는 특성 중요도를 사용
- 항상 양수 값을 가지며, 특성이 얼마나 일찍 그리고 자주 분기에 사용되는지 결정하는 값
Day 2
Random forest
warm up
Random forest made out Decision tree
Decision tree is not flexible when it comes to classifying new samples -> Overfitting problem
Random forest can fix this problem easily
Bagging : Bootstarpping the data(ramdomly selecting data while allowing duplicate) plus using the aggregate to make decision
Out-Of-Bag dataset : it didn't make it into the bootstrap dataset
Out-Of-Bag error : the proportion of Out-Of-Bag samples that were incorrectly classified
- we can measure how accurate our random forest is by the proportion of Out-Of-Bag samples that were correctly classified by the random forest
랜덤포레스트는 앙상블 방법
-
앙상블 방법은 한 종류의 데이터로 여러 머신러닝 학습모델(weak base learner, 기본모델)을 만들어 그 모델들의 예측결과를 다수결이나 평균을 내어 예측하는 방법을 의미
-
이론적으로 기본모델 몇가지 조건을 충족하는 여러 종류의 모델을 사용할 수 있음
-
랜덤포레스트는 결정트리를 기본모델로 사용하는 앙상블 방법이라 할 수 있음
-
결정트리들은 독립적(= 병렬)으로 만들어지며 각각 랜덤으로 예측하는 성능보다 좋을 경우 랜덤포레스트는 결정트리보다 성능이 좋음
-
앙상블 모델에는 bagging, boosting, stacking 모델이 있고, 랜덤포레스트는 bagging 모델에 해당
왜 하나의 좋은 모델을 만들지 않고 기본모델을 만들까?
-> 안정성, 오류를 줄이기 위해, 과적합을 방지하려고 ...
-> 전문가 한명이 모든 문제를 해결하는 것보다 일반인 여러명이 모여 문제를 해결하면 더 좋은 결과를 도출할 수 있기 때문
랜덤포레스트의 기본모델 어떻게 만들까

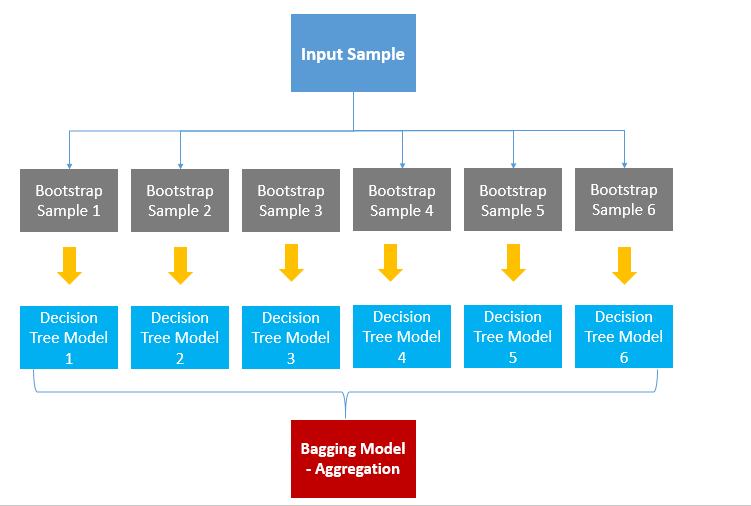
배깅(Bagging, Bootstrap Aggregating)
부트스트랩 방식으로 샘플들을 복원추출해서 트리를 만들고 결과를 도출
데이터에서 샘플 추출 : 부트스트랩 -> 기본모델(결정트리) 만듦 -> 종합 : 평균, 최빈값
부트스트랩(Bootstarp) 샘플링
앙상블에 사용하는 작은 모델들은 부트스트래핑(bootstraping)이라는 샘플링과정으로 얻은 부트스트랩세트를 사용해 학습
- 원본 데이터에서 샘플링을 하는데 복원추출을 한다는 것인데 복원추출은 샘플을 뽑아 값을 기록하고 제자리에 돌려놓는 것을 의미
- 이렇게 샘플링을 특정한 수 만큼 반복하면 하나의 부트스트랩세트가 완성
- 복원추출이기 때문에 부트스트랩세트에는 같은 샘플이 반복될 수 있음

-
부트스트랩세트의 크기가 n이라 할 때 한 번의 추출과정에서 어떤 한 샘플이 추출 되지 않을 확률은
-
n회 복원추출을 진행했을 때 그 샘플이 추출되지 않았을 확률은
-
n을 무한히 크게 했을 때 (참고: )
-
데이터가 충분히 크다고 가정했을 때 한 부트스트랩세트는 표본의 63.2% 에 해당하는 샘플을 가짐
-
추출되지 않은 36.8% 의 샘플이 Out-Of-Bag 샘플
- Out-Of-Bag 검증
pipe.named_steps['randomforestclassifier'].oob_score_ - 포함된 데이터가 샘플을 추출할때마다 바뀌기 때문에 val_score 랑 다를 수 밖에 없음
- validation data 를 나누기 힘들 때(=데이터 크기가 너무 작을 때) val_score 를 oob_core로 대신할 수도 있음 (-> 엄연히 말하면 둘은 다른 것)
- Out-Of-Bag 검증
Agrregation
- 부트스트랩세트로 만들어진 기본모델을 합치는 과정
- 회귀문제일 경우 기본모델 결과들의 평균으로 결과를 내고
- 분류문제일 경우 다수결로 가장 많은 모델들이 선택한 범주로 예측
랜덤포레스트는 기본모델의 트리를 만들 때 무작위로 선택한 특성세트 사용
- 결정트리에서 분할을 위한 특성을 선택할 때 모든 특성(n개)을 고려하여 최적의 특성을 고르고 분할
- 랜덤포레스트에서는 특성 n개 중 일부분 k개의 특성을 선택(sampling) 하고 이 k개에서 최적의 특성을 찾아내어 분할 (k개는 일반적으로 를 사용)
순서형(ordinal) 인코딩
- 순서형 인코딩은 범주에 숫자를 맵핑
- ['a','b','c'] -> [1,2,3] 으로 인코딩
- 트리구조에서는 중요한 특성이 상위노드에서 먼저 분할이 일어나기 때문에 범주 종류가 많은 (high carinality) 특성은 one-hot encoding 으로 인해 상위노드에서 선택될 기회가 적어짐
- 때문에 one-hot encoding 영향을 안 받는 수치형 특성이 상위노드를 차지할 기회가 높아지고 전체적인 성능 저하 생길 수 있음
- one-hot encoding : 특성의 수 증가
- ordinal encodng : 특성의 수 불변
- 범주들을 순서가 있는 숫자형으로 바꾸면 원래 그 범주에 없던 순서정보가 생김
- 순서형 인코딩은 범주들 간의 분명한 순위가 있을 때 그 연관성에 맞게 숫자를 정해주는 것이 좋음
- 명목형 변수에도 ordinal encoding 사용해도 되는 이유
-> 숫자의 크기가 의미가 없어서, 분할을 기준에 순서의 개념이 들어간다 해서 집단이 나뉘는 그룹이 달라지지 않음, 거리나 위치가 중요한 모델이 아니기 때문- ordinal encoding 을 one-hot encoding 보다 권장하는 이유
-> 피쳐 수 늘어나지 않아 특성 중요도를 정확하게 파악할 수 있기 때문
특성 중요도(Importance)
- 중요도는 노드들의 지니불순도(Gini impurity) 를 통해 계산
- 노드가 중요할수록 불순도가 크게 감소
트리 앙상블 모델이 결정트리 모델보다 상대적으로 과적합을 피할 수 있는 이유
- 결정트리 모델은 데이터 일부를 과적합하는 경향이 있음
- 랜덤포레스트는 다르게 샘플링된 데이터로 과적합된 트리를 많이 만들고 그 결과를 평균 내 사용하는 모델임
- 랜덤포레스트에서 트리를 랜덤하게 만드는 방법
- 랜덤포레스트에서 학습되는 트리들은 배깅을 통해 만들어지는데(bootstrap = true) 이때 각 기본트리에 사용되는 데이터가 랜덤으로 선택
- 각각 트리는 무작위로 선택된 특성들을 가지고 분기를 수행(max_features = auto)
랜덤포레스트 모델이 과적합에 결정트리에 비해 더 강한 이유?
- 여러 모델을 종합한 것이기 때문에 에러를 발견하고 보완할 확률이 더 높음
- 전체 데이터를 모두 사용하지 않기 때문
- 편향이 높은 약한 기준모델 여러 개를 종합하기 때문
Day 3
Evaluation Metrics for Classification
warm up
Performance measure
1. Classification : simple accuracy, precision, recall, F-beta measure, ROC(& AUC)
2. Regression : sum of squares error, mean absolute error, RMS error
Confusion Matrix
- Sklearn.metrics.plot_confusion_matrix
- Accuracy = accuracy_score()
- 정확도(Accuracy) : 전체 범주를 모두 바르게 맞춘 경우를 전체 수로 나눈 값
- 정밀도(Precision) : Positive로 예측한 경우 중 올바르게 Positive를 맞춘 비율
- 재현율(Recall, Sensitivity) : 실제 Positive인 것 중 올바르게 Positive를 맞춘 것의 비율
- F1점수(F1 score) : 정밀도와 재현율의 조화평균(harmonic mean) =
- F-beta score :
- 재현율에 정밀도의 2배 가중치 -> beta = 2
- 정밀도에 재현율의 2배 가중치 -> beta = 0.5
다루는 문제에 따라 정밀도와 재현율 중 어느 평가지표를 우선시 해야하는지 판단해야 함
- 병원에서 초기 암진단을 하는 경우?
- recall -> 초기 발견이 사망률을 크게 낮추기 때문에(실제 암일때 암이 아니라고 진단하면 리스크가 크기 때문에)
- 넷플릭스에서 영화추천을 해주는 경우?
- precision -> 선호하지 않은 영화를 추천하는 경우 소비자가 탈퇴할 가능성이 높기 때문
임계값(Threholds)
이분법으로 확실히 분류를 할 기준, Randomforestclassifier 기본 임계값은 0.5
- 임계값이 높아질수록 정밀도 높아지고 재현율 감소(1을 기준으로, 0을 기준으로 하면 반대)
ROC curve & AUC score
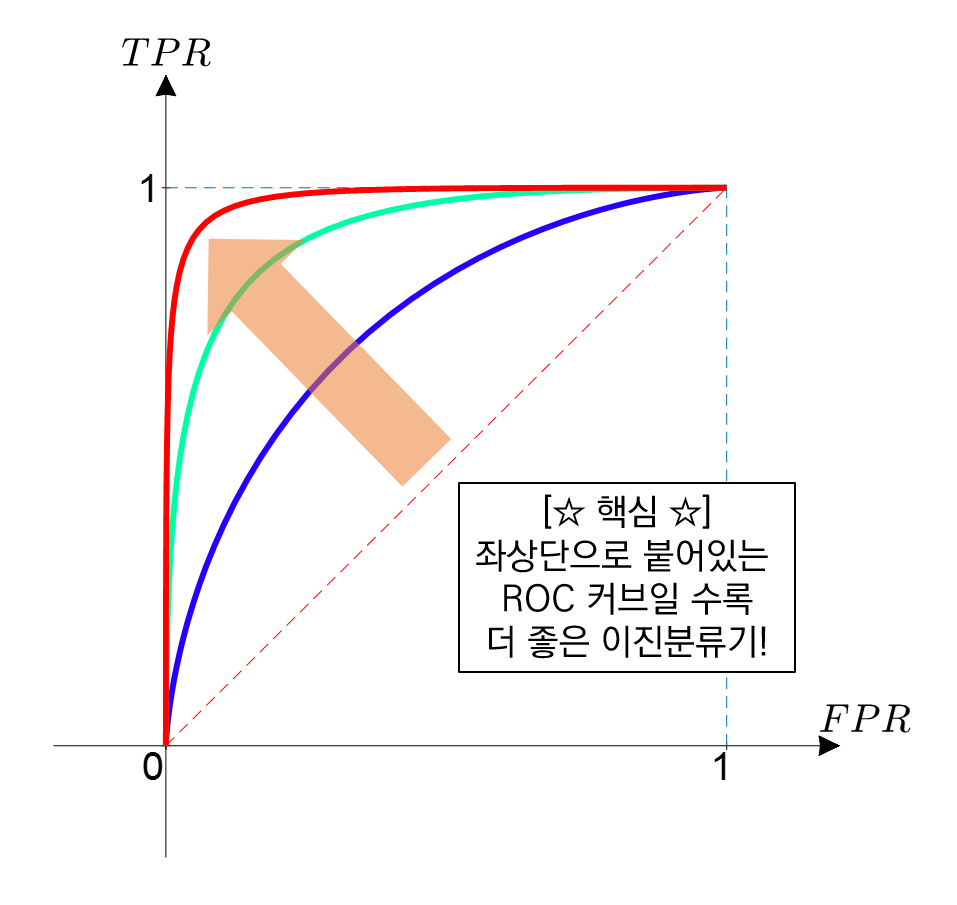 모든 임계값을 한 눈에 보고 모델을 평가할 수 있는 방법
모든 임계값을 한 눈에 보고 모델을 평가할 수 있는 방법
이진분류 문제에서 사용 가능(다중분류 문제에서는 각 클래스를 이진클래스 분류 문제로 변환하여 구할 수 있음)
ROC curve는 여러 임계값에 대해 TPR(True Positive Rate) 과 FPR(False Positive Rate) 그래프 보여줌
Recall(재현율) = Sensitivity =
Fall-out(위양성률) =
-
재현율을 높이기 위해서는 Positive로 판단하는 임계값을 계속 낮추어 모두 Positive로 판단하게 만들면 됨
- 하지만 이렇게 하면 동시에 Negative이지만 Positive로 판단하는 위양성률도 같이 높아짐
-
재현율은 최대화 하고 위양성률은 최소화 하는 임계값이 최적의 임계값
#threshold 최대값의 인덱스,np.argmax()
optimal_idx = np.argmax(tpr - fpr)
optimal_threshold = thresholds[optimal_idx]- AUC 는 ROC curve의 아래 면적

- from sklearn.metrics import roc_curve
- from sklearn.metrics import roc_auc_curve
ML 모델 flow
1. 전처리, eda
2. 모델: 평가지표-정밀도, roc,auc
3. val_set 검증 - 정밀도 (:과적합 성능 낮음 등등 문제)
4. 모델 수정, 발전 : 피쳐엔지니어링, 하이퍼파라미터조정, 로지스틱, 부스팅 등
5. (3, 4번) 반복
6. 최종모델
7. 임계값 조정 roc cuve(임계값 조정 위해서) : 최최종모델
8. 테스트 : 결과(정밀도)
9. 모델 해석
Day 4
Model Selection
warm up
Cross-validtion allows us to compare different machine learning methods and get a sense of how well they wll work in practice
교차검증(Cross-validation)
- 모델선택에 대한 문제 해결하기 위한 사용 방법 중 하나
- hold-out 교차검증 : 훈련/검증/테스트 셋으로 나누어 학습 진행
- 훈련셋의 크기가 모델학습에 충분하지 않을 경우 문제 발생할 수 있음
- 검증셋 크기가 충분히 크지 않다면 예측 성능에 대한 추정 부정확
- K-fold 교차검증 : 데이터를 k개로 등분하여 k개의 집합에서 k-1개의 부분집합을 훈련에 사용하고 나머지 부분집합을 테스트 데이터로 검증
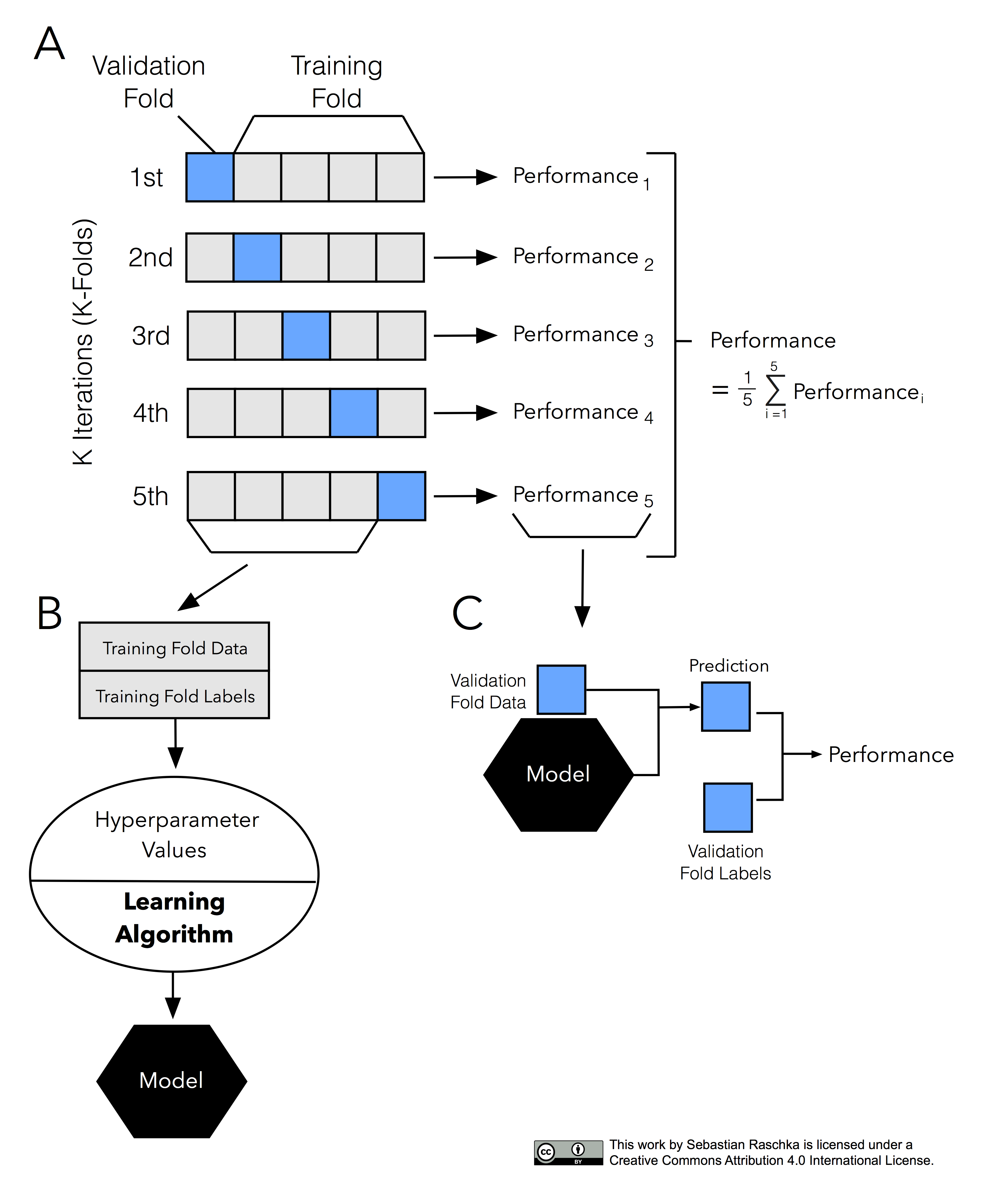
A : K개로 데이터를 나눈 후, 그 중 하나는 검증데이터로 나머지는 훈련데이터로 사용
B : 하이퍼파라미터를 설정해 학습을 시켜 모델 생성
C : 여기서 학습된 모델과 검증 데이터를 사용해 데이터 예측
-> 이런 퍼포먼스들을 모두 함쳐서 평균을 냄 = 종합적인 검증 스코어
- sklearn cross_val_score
- 시계열 데이터에는 적합하지 않음
모델선택(Model selection) : 문제를 풀기 위해 어떤 학습 모델을 사용할 것인지, 어떤 하이퍼파라미터를 사용할 것인지
TargetEncoder : 범주형 변수 인코더로 타겟값을 특성의 범주별로 평균을 내어 그 값으로 인코딩
하이퍼파라미터 튜닝
머신러닝 모델을 만들 때 중요한 이슈는 최적화와 일반화
- 최적화 : 훈련 데이터로 더 좋은 성능을 얻기 위해 모델 조정하는 과정
- 일반화 : 학습된 모델이 처음 본 데이터에서 얼마나 좋은 성능을 내는지
이상적인 모델은 과소적합과 과적합 사이에 존재

검증곡선 : 훈련/검증데이터에 대해 y축: 스코어 ,x축: 하이퍼파라미터로 그린 그래프
훈련곡선(learning curve): x축이 훈련데이터 수(# of training samples)에 대해 그린 것
Scikit-learn,validation curves 를 사용하면 다양한 하이퍼파라미터 값에 대해 훈련/검증 스코어 값의 변화를 확인할 수 있음
여러 하이퍼파라미터의 최적값 찾기 (모델 훈련 중에 학습이 되지 않는 파라미터)
사이킷런 하이퍼파라미터 튜닝 툴
- GridSearch CV : 검증하고 싶은 하이퍼파라미터들의 수치를 정해주고 그 조합을 모두 검증
- Randomized Search CV : 검증하려는 하이퍼파라미터들의 값 범위를 지정해주면 무작위로 값을 지정해 그 조합을 모두 검증
RandomizedSearchCV(모델명, param_distributions=하이퍼파라미터 조정범위
,n_iter = "탐색횟수", cv = "폴드 수", scorig = "평가방법"
,verbose = "진행 상황 표시", random_state = "시드")- n_iter = 50, cv = 2 / n_iter = 10, cv = 10
#Ridge 회귀모델의 하이퍼파라미터 튜닝 예시
from sklearn.model_selection import RandomizedSearchCV
from category_encoders import OneHotEncoder
from sklearn.feature_selection import f_regression, SelectKBest
from sklearn.impute import SimpleImputer
from sklearn.linear_model import Ridge
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
pipe = make_pipeline(
OneHotEncoder(use_cat_names=True)
, SimpleImputer()
, StandardScaler()
, SelectKBest(f_regression)
, Ridge()
)
# 튜닝할 하이퍼파라미터의 범위를 지정해 주는 부분
dists = {
'simpleimputer__strategy': ['mean', 'median'],
'selectkbest__k': range(1, len(X_train.columns)+1),
'ridge__alpha': [0.1, 1, 10],
}
clf = RandomizedSearchCV(
pipe,
param_distributions=dists,
n_iter=50,
cv=3,
scoring='neg_mean_absolute_error',
verbose=1,
n_jobs=-1
)
clf.fit(X_train, y_train);
print('최적 하이퍼파라미터: ', clf.best_params_)
print('MAE: ', -clf.best_score_)
# n_iter * cv = tasks 수행 수# 랜덤포레스트 회귀문제 적용 예시
from scipy.stats import randint, uniform
pipe = make_pipeline(
TargetEncoder(),
SimpleImputer(),
RandomForestRegressor(random_state=2)
)
dists = {
'targetencoder__smoothing': [2.,20.,50.,60.,100.,500.,1000.], # int로 넣으면 error(bug)
'targetencoder__min_samples_leaf': randint(1, 10),
'simpleimputer__strategy': ['mean', 'median'],
'randomforestregressor__n_estimators': randint(50, 500),
'randomforestregressor__max_depth': [5, 10, 15, 20, None],
'randomforestregressor__max_features': uniform(0, 1) # max_features
}
clf = RandomizedSearchCV(
pipe,
param_distributions=dists,
n_iter=50,
cv=3,
scoring='neg_mean_absolute_error',
verbose=1,
n_jobs=-1
)
clf.fit(X_train, y_train);
print('최적 하이퍼파라미터: ', clf.best_params_)
print('MAE: ', -clf.best_score_)negative MAE 사용 이유
사이킷런의 모델들은 성능을 평가하는 수치가 크면 좋다고 인식
하지만 mae같은 지표들(비용함수)은 작으면 작을수록 좋다. 0.3이 10보다 좋은 거지만 모델은 10이 더 좋다고 인식할수도 있는 것
그래서 성능 평가 지표에 -를 취해준 negative mae같은 것을 지표로 사용
그렇게 되면 -0.3이 -10보다 큰 거라 0.3이 더 좋다고 인식하고 실제로도 그게 맞기 때문!
예측결과 : best_estimator _
best_estimator _ : CV가 끝난 후 찾은 best parameter를 사용해 모든 학습데이터(all the training data)를 가지고 다시 학습(refit)한 상태
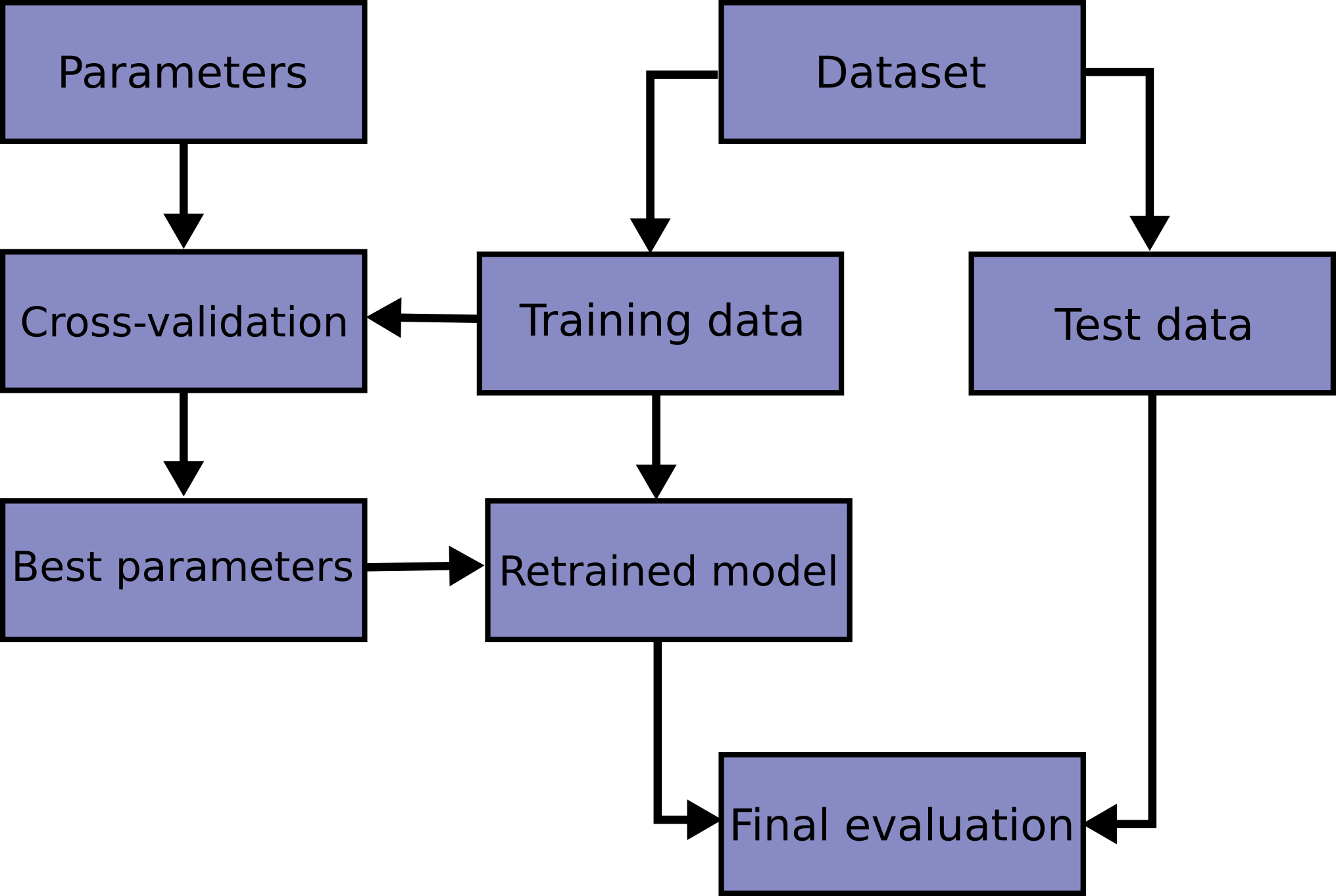
만약 hold-out 교차검증(훈련/검증/테스트 세트로 한 번만 나누어 실험)을 수행한 경우에는, (훈련 + 검증) 데이터셋에서 최적화된 하이퍼파라미터로 최종 모델을 재학습(refit) 해야함
선형회귀, 랜덤포레스트 모델들의 튜닝 추천 하이퍼파라미터
Random Forest
- class_weight (불균형(imbalanced) 클래스인 경우)
- max_depth (너무 깊어지면 과적합)
- n_estimators (적을경우 과소적합, 높을경우 긴 학습시간)
- min_samples_leaf (과적합일경우 높임)
- max_features (줄일 수록 다양한 트리생성)
Logistic Regression
- C (Inverse of regularization strength)
- class_weight (불균형 클래스인 경우)
- penalty
Ridge / Lasso Regression
- alpha
