1. 퀵 정렬

• 분할 정복 알고리즘
• 불안정 정렬에 속하며, 다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬에 속함
• Merge Sort와 달리 Quick Sort는 배열을 비균등하게 분할
• 장점✨
  1. 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환할 뿐만 아니라, 한 번 결정된 피봇들이 추후 연산에서 제외되는 특성 때문에 시간복잡도가 같은 다른 정렬 알고리즘보다 빠름.
  2. 다른 메모리 공간이 필요없음.
• 단점🧐
  1. 불안정 정렬 - 동일한 값에 대해서 기존의 순서가 유지되지 않음.
  2. 최악의 경우 O(n^2)의 시간복잡도가 나옴.

퀵정렬 Process (Ascending)

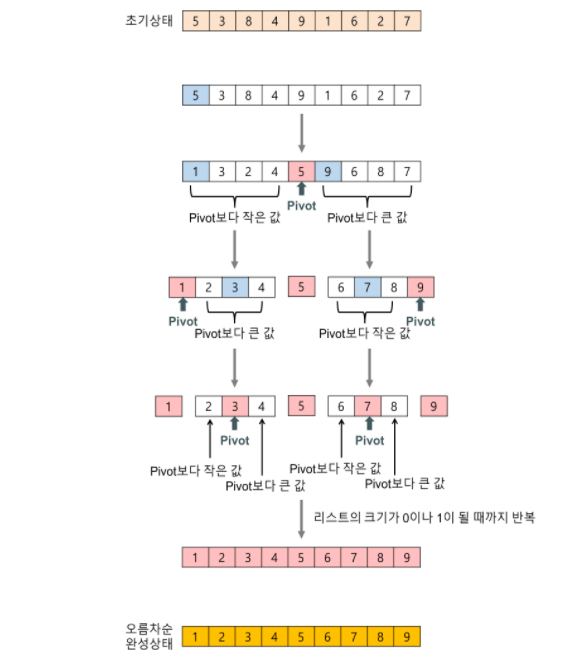
1. 리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 pivot(피벗) 이라고 한다.

2. pivot을 기준으로 pivot보다 작은 요소들은 모두 pivot의 왼쪽으로 옮기고 pivot보다 큰 요소들은 모두 pivot의 오른쪽으로 옮긴다.

3. pivot을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.
   3-1) 분할된 왼쪽 리스트와 오른쪽 리스트도 다시 pivot을 정하고 pivot을 기준으로 2개의 부분리스트로 나눈다.
   3-2) 재귀를 사용하여 부분 리스트들이 더이상 분할이 불가능 할 때까지 반복한다.

Python 코드

def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    lesser_arr, equal_arr, greater_arr = [], [], []
    for num in arr:
        if num < pivot:
            lesser_arr.append(num) // 분할정복
        elif num > pivot:
            greater_arr.append(num) // 분할정복
        else:
            equal_arr.append(num)
    return quick_sort(lesser_arr) + equal_arr + quick_sort(greater_arr)

복잡도

• 공간복잡도
  : 재귀적으로 정의되므로 재귀 호출에 따른 스택이 사용됨. 스택의 깊이는 n개의 원소에 대해 log(n)에 비례

  O(nlog(n))

• 시간복잡도

  최악의 경우(pivot이 최솟값이나 최댓값 선정) : O(n^2)
  평균 : O(nlog(n))

2. 병합정렬

• 분할(split) 단계와 방합(merge) 단계로 나눌 수 있으며, 단순히 중간 인덱스를 찾아야 하는 분할 비용보다 모든 값들을 비교해야해서 비용이 큼.
• 인접한 값들 간에 상호 자리 교대(swap)이 일어나지 않음.
• 최악의 경우 O(n^2)인 퀵정렬에서 보완하여 모든 경우에 log(nlog(n))을 보장
• 장점✨
  1. O(nlogn)의 시간 복잡도를 보장.
• 단점🧐
  1. 임시 배열이 필요하므로 추가 공간이 필요하다 → 추가 공간을 사용하므로 제자리 정렬이 아니다
  2. 데이터의 크기가 큰 경우 이동 횟수가 많으므로 시간 낭비 발생

병합정렬 Process (Ascending)

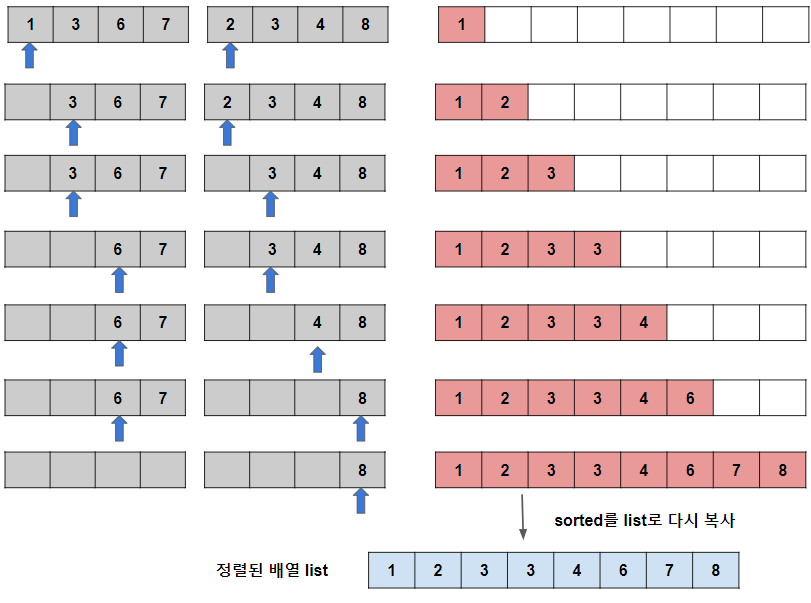
• 주어진 배열을 원소가 하나 밖에 남지 않을 때까지 계속 둘로 쪼갠 후에 다시 크기 순으로 재배열 하면서 원래 크기의 배열로 합침.

1. 두 개의 리스트의 값을 처음부터 비교해서 두 개의 리스트의 값 중에 작은 값을 새로운 리스트로 옮긴다.
2. 두 개의 리스트 중 하나의 리스트가 끝날 때까지 반복한다.
3. 하나의 리스트가 끝나게 되면 남은 리스트의 값을 모두 새로운 리스트로 옮긴다.

Python 코드

1. 메모리 효율이 안좋음
def merge_sort(arr):
    if len(arr) < 2:
        return arr

    mid = len(arr) // 2
    low_arr = merge_sort(arr[:mid])
    high_arr = merge_sort(arr[mid:])

    merged_arr = []
    l = h = 0
    while l < len(low_arr) and h < len(high_arr):
        if low_arr[l] < high_arr[h]:
            merged_arr.append(low_arr[l])
            l += 1
        else:
            merged_arr.append(high_arr[h])
            h += 1
    merged_arr += low_arr[l:]
    merged_arr += high_arr[h:]
    return merged_arr
    
2. 최적화
def merge_sort(arr):
    def sort(low, high):
        if high - low < 2:
            return
        mid = (low + high) // 2
        sort(low, mid)
        sort(mid, high)
        merge(low, mid, high)

    def merge(low, mid, high):
        temp = []
        l, h = low, mid

        while l < mid and h < high:
            if arr[l] < arr[h]:
                temp.append(arr[l])
                l += 1
            else:
                temp.append(arr[h])
                h += 1

        while l < mid:
            temp.append(arr[l])
            l += 1
        while h < high:
            temp.append(arr[h])
            h += 1

        for i in range(low, high):
            arr[i] = temp[i - low]

    return sort(0, len(arr))

복잡도

• 공간복잡도
  : 두 개의 배열을 병합할 때 병합 결과를 담아 놓을 배열이 추가로 필요

  O(N)

• 시간복잡도

  O(nlog(n))