Dynamic Programming
DP는 하나의 문제를 여러 개의 하위 문제로 나눠 계산한 뒤, 이 결과를 재사용하여 문제를 효율적으로 해결하는 알고리즘 기법입니다. 동일한 하위 문제가 여러 번 반복되는 경우, 계산 결과를 테이블에 저장해 중복 계산을 피합니다.
최적화 문제
DP는 주로 최적화 문제 풀이와 관련 있습니다. 여러 개의 해답 중 최대(최소) 값을 구하거나, 이 때 최적의 해답을 계산하는 데 사용됩니다.
DP의 두 가지 구현 방식
1. Tabulation
- 가장 작은 하위 문제부터 차례대로 계산해 테이블을 채워나가는 방식
- 보통 반복문을 사용해 구현
- 테이블을 기반으로 순차적으로 큰 문제를 해결
2. Memoization
- 큰 문제를 먼저 호출한 뒤, 필요한 경우에만 하위 문제를 재귀 호출하여 해결하는 방식
- 계산한 하위 문제의 결과를 테이블에 저장
- 필요할 때만 계산하고 저장하며, 이미 계산된 값은 재사용
f(4)→f(3)→f(2)…
DP 해결 시나리오
step1. 구조를 분석하기 (Top-Down)
- 최적값과 최적의 해답을 어떻게 구할 수 있을지 분석하는 단계입니다.
- Top-Down 방식으로 해결하며, 목표를 역방향으로 추적합니다.
step2. 최적 값을 재귀식으로 정의하기
- 최적 값을 Top-Down 방식으로 분석하여 재귀식을 정의합니다.
step3. 상향식으로 최적값 계산하기 (Bottom-Up)
- 재귀식으로 정의된 최적값을 Bottom-up으로 계산합니다.
- 테이블을 이용하여 하위 문제 → 상위 문제를 해결합니다.
(필요한 경우 )step4. 최적의 해답 계산하기(Reconstruct)
step3의 최적 값을 계산하는 과정에서 발생하는 정보를 이용하여 구합니다.
[문제.1] 2XN 직사각형 타일 채우기
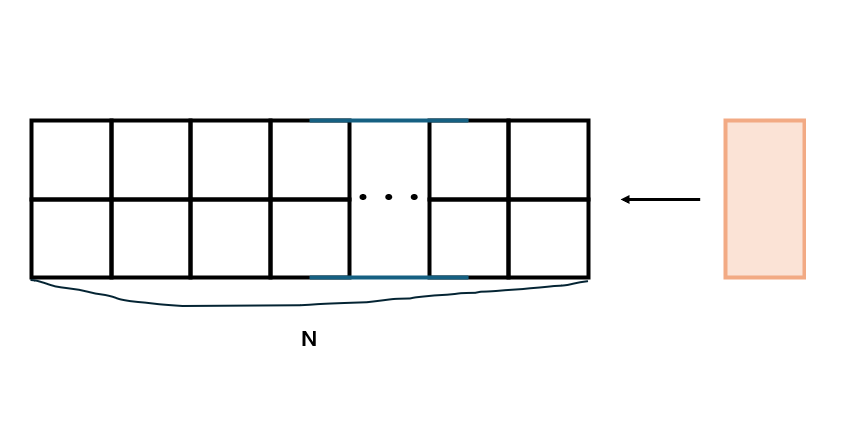
크기가 2 X N 인 직사각형의 판이 주어졌을 때, 이 판을 2 X 1 타일로 채우는 경우의 수를 구하는 문제입니다.
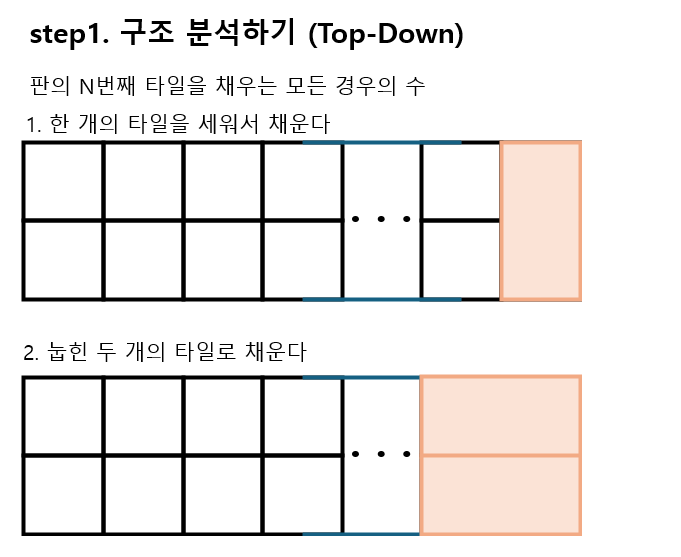
step1. 구조 분석하기 (Top-Down)
- 도미노 : 2 X 1 크기, 판 크기 2 X N
- 길이가 N인 판을 채우는 경우의 수는 두 가지로 나눌 수 있다
- 마지막 타일이 세워진 경우
- 마지막 타일이 눕힌 두 개의 타일인 경우
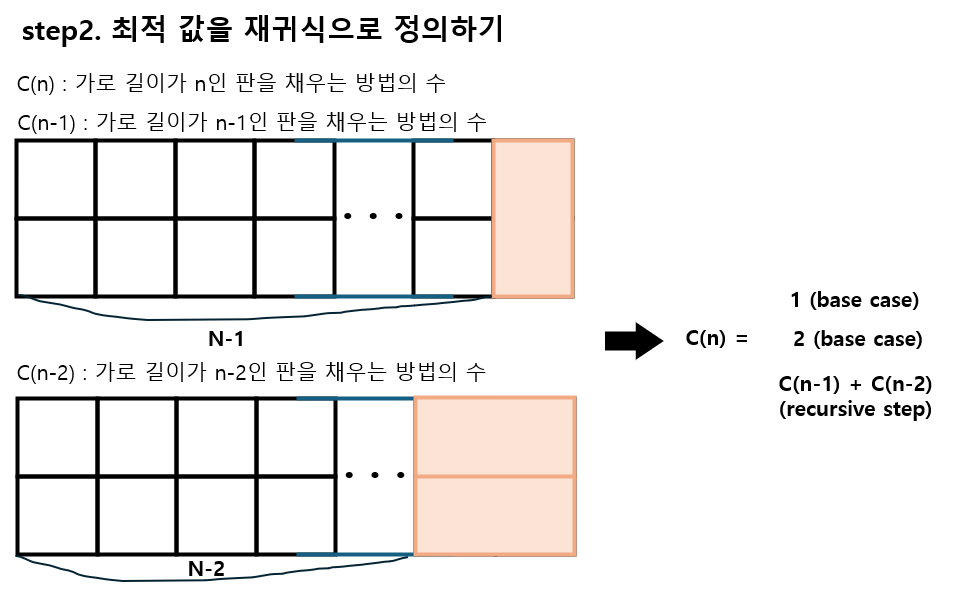
step2. 최적 값을 재귀식으로 정의하기
C(n): 가로가 n인 판을 채우는 방법의 수라고 정의한다.
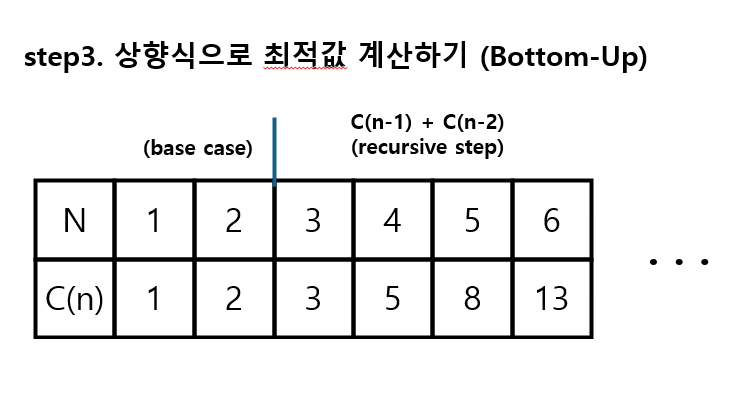
step3. 상향식으로 최적값 계산하기(Bottom-Up)
- C[n] : 가로의 길이가 n인 판을 2 X 1 타일로 채우는 경우의 수를 저장하는 테이블로 정의한다
- 재귀식 → 테이블 변환하기 :
C(n)→C[n] - 가로의 길이가 1인 판을 채우는 방법은 1개, 2인 판을 채우는 방법은 2개이다. base case가 설정됐으니 순차적으로
C[n] = C[n-1] + C[n-2]로 구하면 된다.
예제 코드
#include <iostream>
#include <vector>
using namespace std;
int tabulation(int n)
{
if (n == 1 || n == 2) return n;
vector<int> vec(n+1, 0);
vec[1] = 1;
vec[2] = 2;
for (int i = 3; i <= n; i++)
{
// 차례대로 값 구하기
vec[i] = vec[i-1] + vec[i-2];
}
return vec[n];
}
int memoization(vector<int>& vec, int n)
{
// 값이 테이블에 존재하는 경우
if (vec[n] != -1) return vec[n];
// 값이 테이블에 없어 구해야 하는 경우
if (n == 1 || n == 2) return vec[n] = n;
return vec[n] = memoization(vec, n-1) + memoization(vec, n-2);
}
int main(void)
{
int n; cin >> n;
cout << tabulation(n) << "\n";
vector<int> memo(n+1, -1);
cout << memoization(memo, n) << "\n";
} [문제.2] 동전 교환 문제 : 1차 동적 계획법
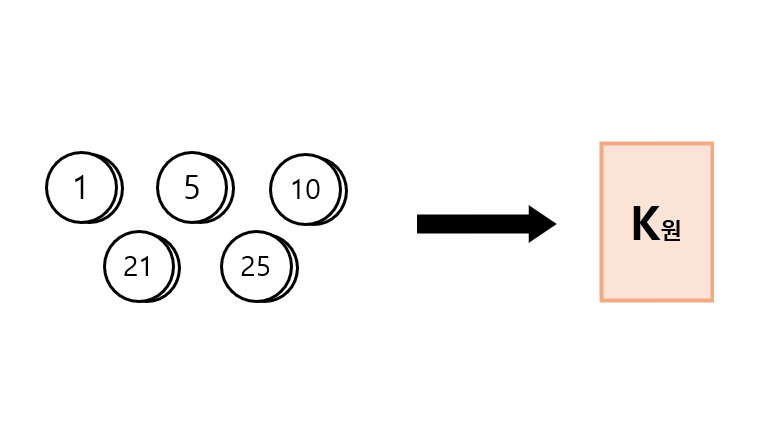
동전의 종류가 { 1원, 5원, 10원, 21원, 25원 } 로 5 개일 때, k원을 만드는 최소 동전 개수를 구한 뒤, 이 때 동전 조합을 구하라.
step1. 구조를 분석하기 (Top-Down)
- 동전의 종류 : 1원 / 5원 / 10원 / 21원 / 25원 … n 개
- 목표 : k원을 구성하기
- k원을 구성하는 최소 동전의 개수는 k원에서 특정 동전 금액을 뺀 값의 최소 동전 개수 + 1이다.
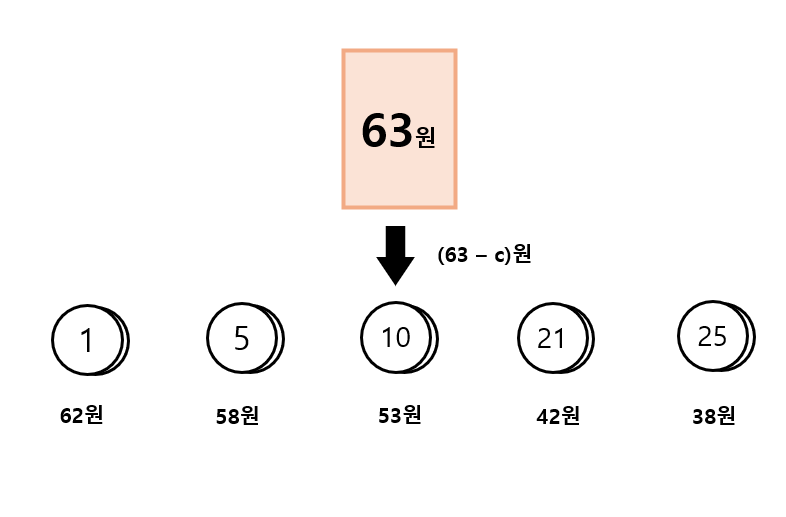
[ 62원, 58원, 53원, 42원, 38원 ]에서 가장 적은 동전으로 만들 수 있는 금액은 42원이다 (21원 + 21원, 2개). 즉, 42원을 구성하는 최소 동전 조합에 21원 동전 한 개를 더해 63원을 만들 수 있다는 의미이다.
step2. 최적 값을 재귀식으로 정의하기
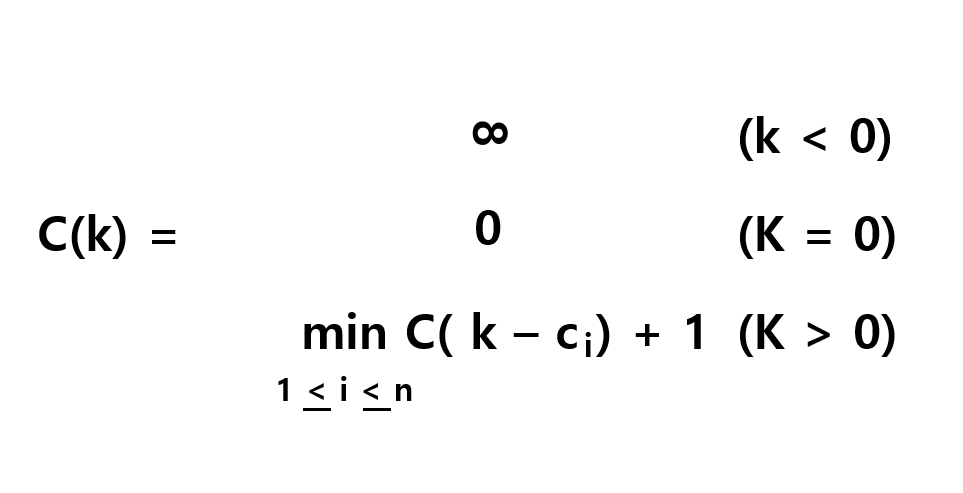
C(k): k원을 구성하기 위한 최소 동전의 개수라고 정의한다.
step3. 상향식으로 최적값 계산하기 (Bottom-Up)
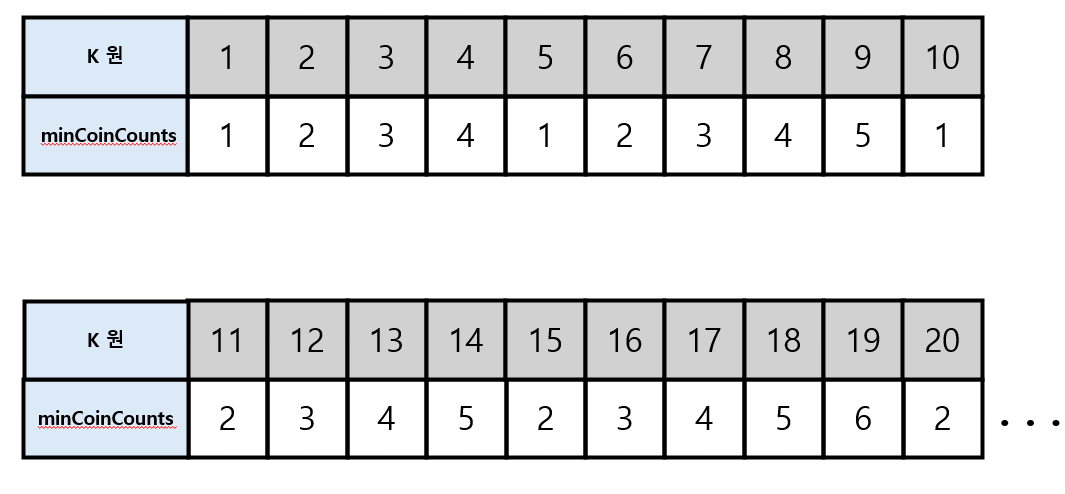
minCoinCounts[k]배열은 k원을 만들기 위한 최소 동전의 개수를 저장한다.- C[12] 는 12원을 만들기 위해 최소 3개의 동전이 필요하다는 뜻이다.
(필요한 경우)step4. 최적의 해답 계산하기(Reconstruct)
- 최적 값을 발견했을 때의 정보를 저장하는 배열
lastUsedCoin에 사용된 금액 기록한다. - 앞의 경우에서는
42원이 2개의 동전으로 구성할 수 있어 최적 값이었다.(63 - 21 = 42)즉,21원짜리 동전을 사용해서42원에 접근했으므로,lastUsedCoin[63] = 21이 된다.63원을 최소 동전 개수로 구성하기 위해 마지막으로 사용한 동전이21원짜리 동전임을 의미한다.
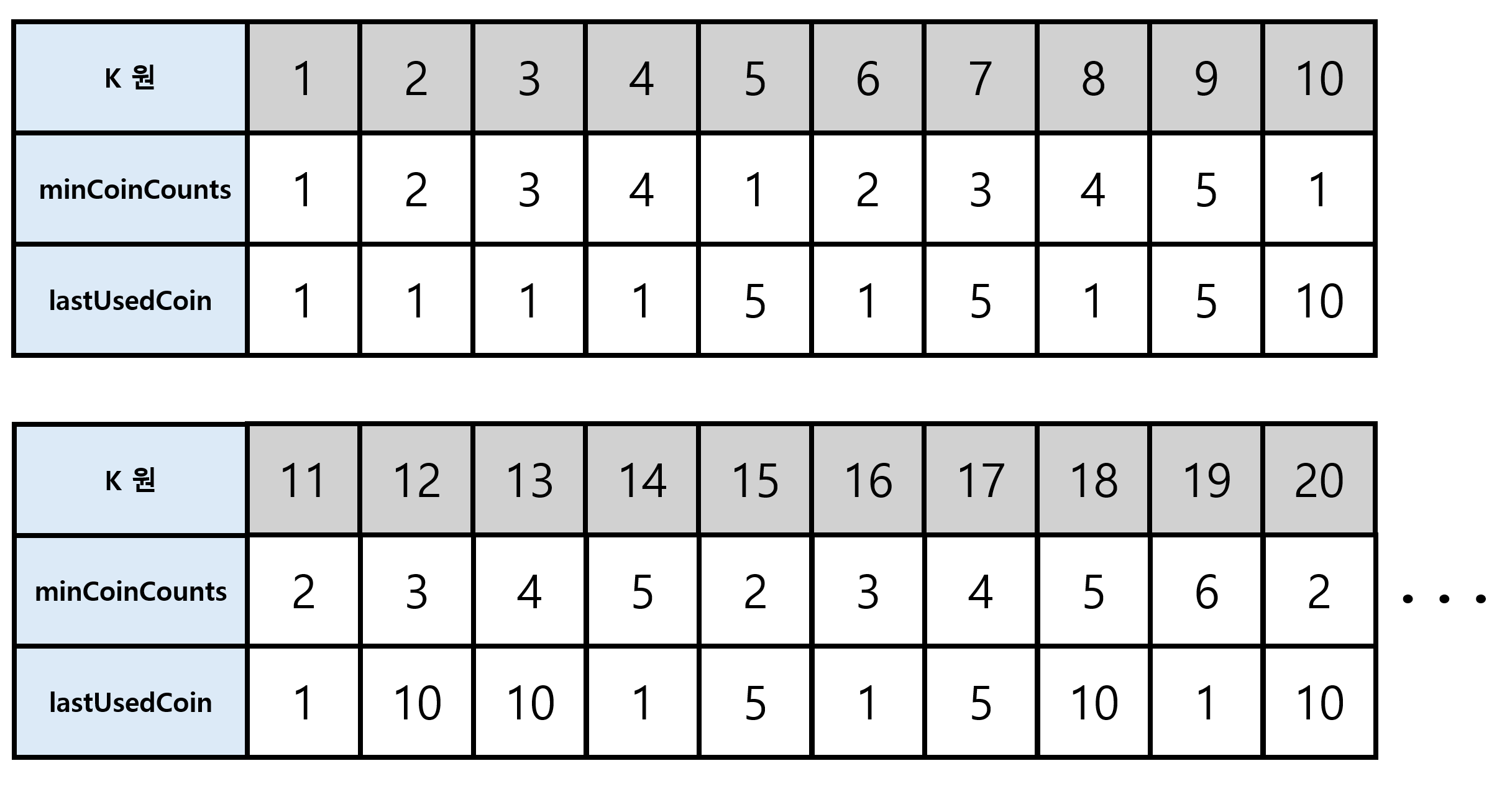
이렇게 작성된 표로, 최적 해답를 구할 수 있다.
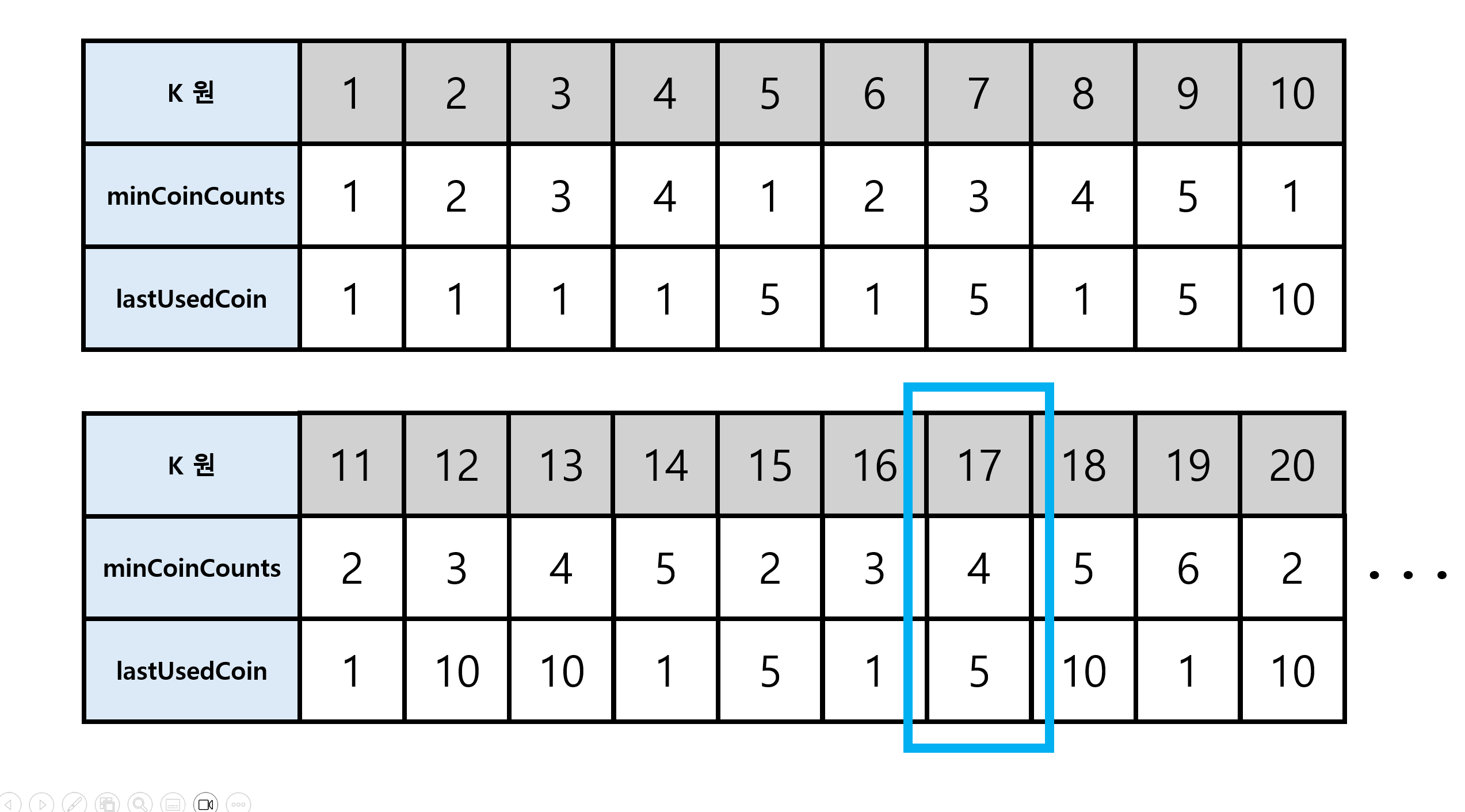
17원을 구성하는 최소 동전 조합을 구하려고 한다.
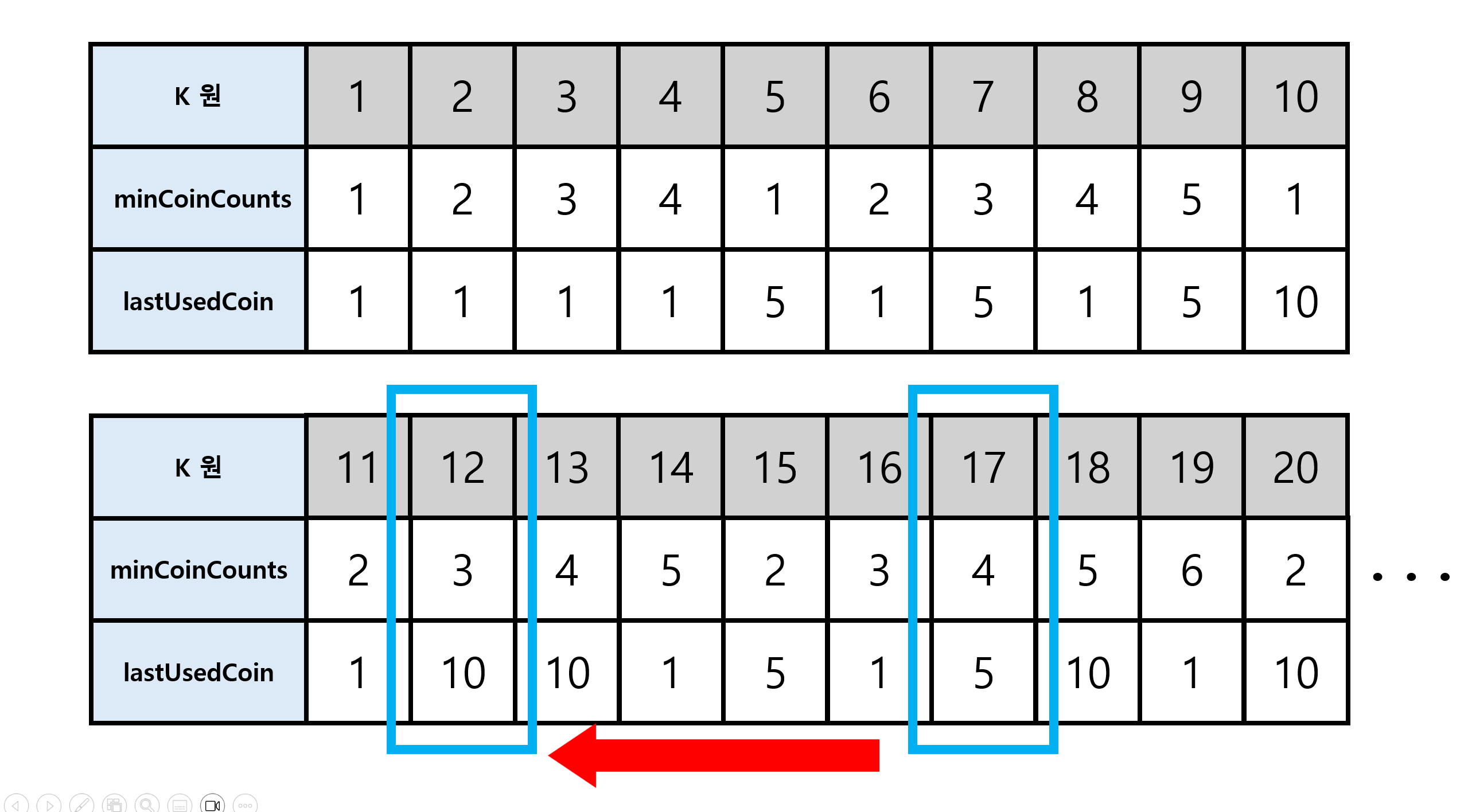
lastUsedCoin[17]이 5이므로, 5원 짜리 동전이 사용됐음을 알 수 있다. 이렇게 역추적을 시작하면
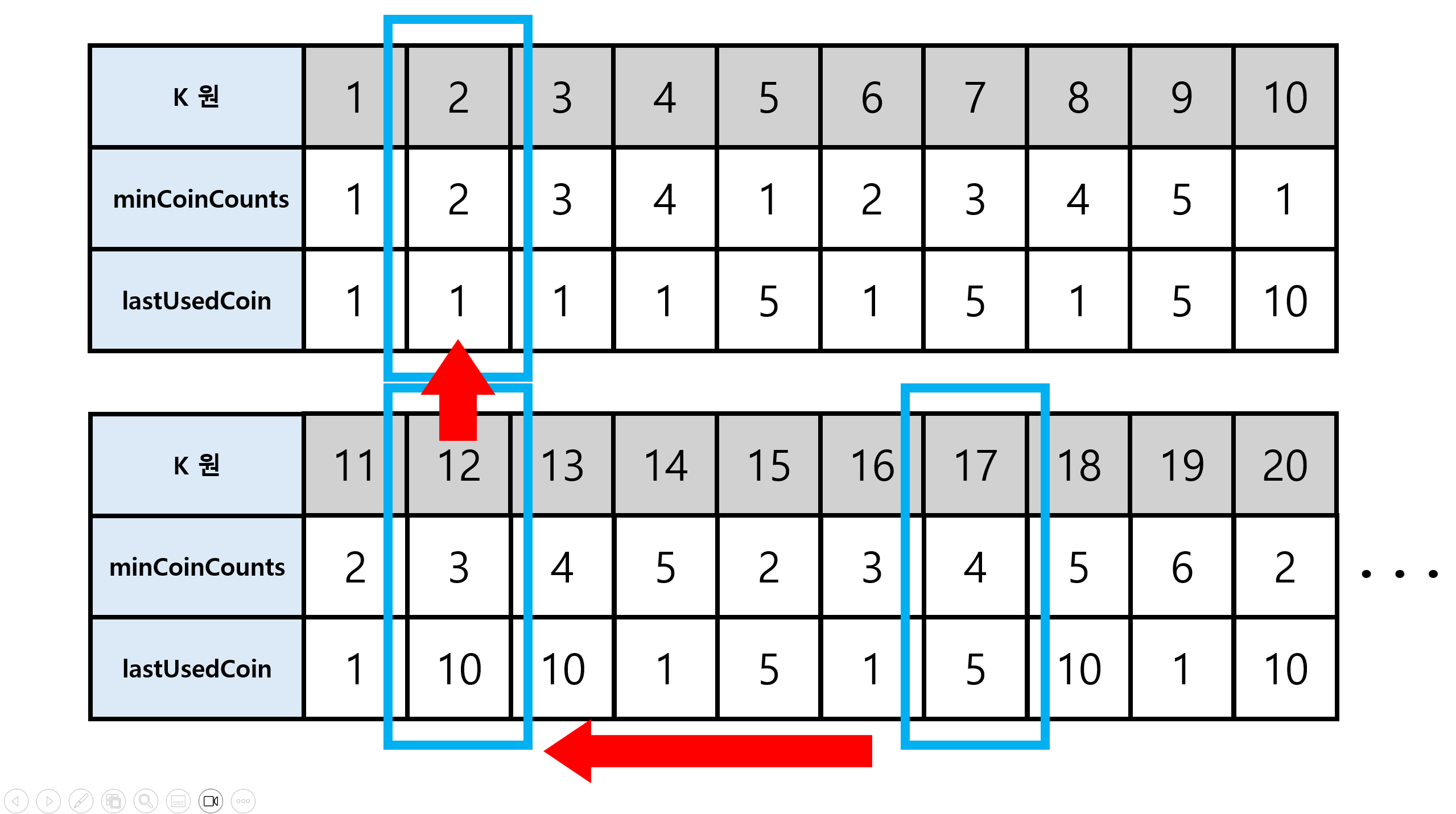
12원을 구성하기 위해선 10원 짜리 동전이 사용됐으며
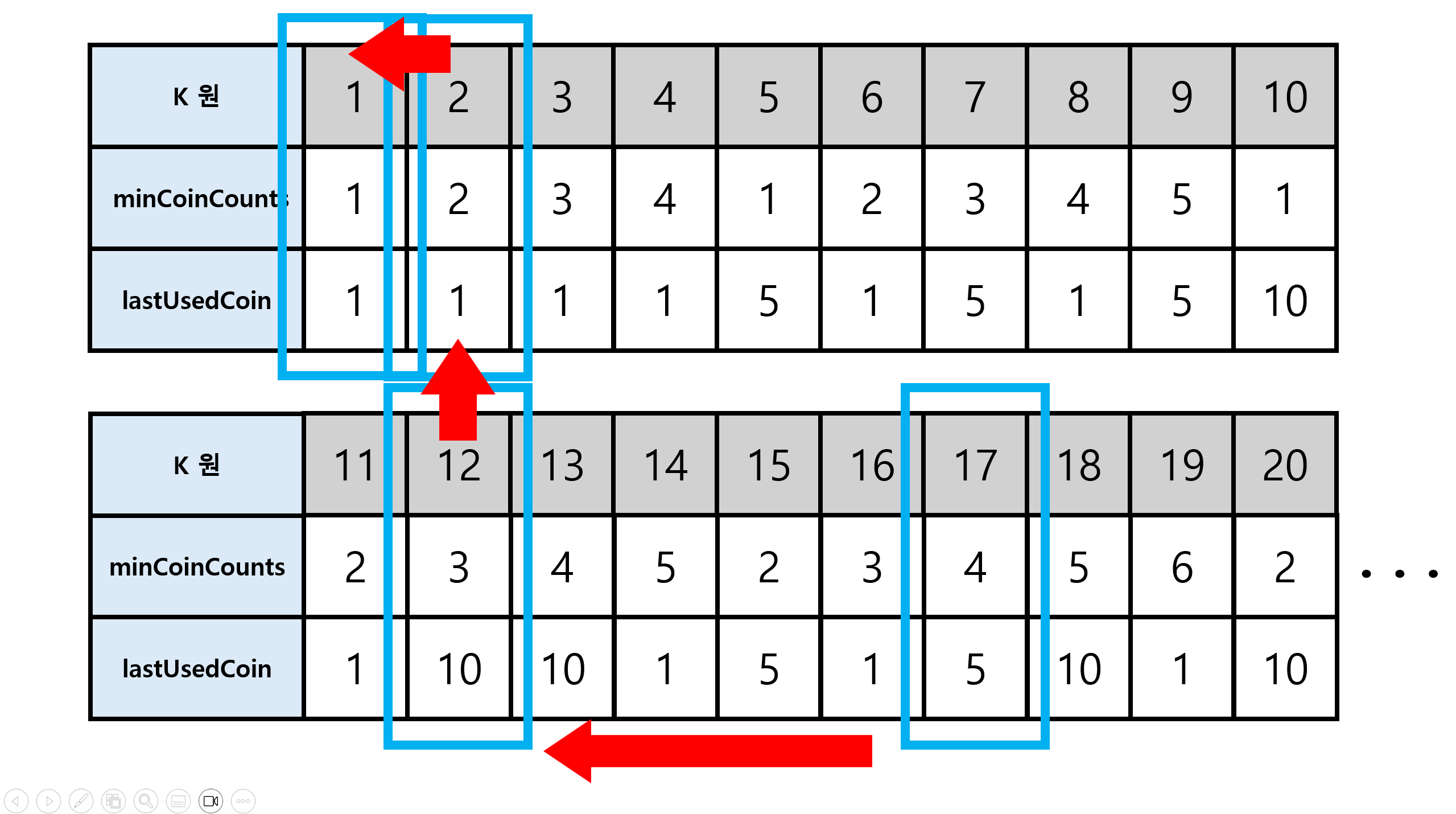
2원 을 구성하기 위해선 1원 짜리 동전이 총 2개 쓰였음을 알 수 있다.
최종적으로 17원 을 구성하는 최소 동전 조합은 [ 1원, 1원, 5원, 10원 ] 총 4개가 필요하다.
예제 코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 사용할 동전 단위
const int coins[] = { 1, 5, 10, 21, 25 };
int totalAmount;
void tabulation()
{
int coinCount = sizeof(coins) / sizeof(coins[0]);
// 각 금액별 최소 동전 수를 저장하는 배열
vector<int> minCoins(totalAmount + 1, 0);
// 각 금액을 만들기 위해 마지막으로 사용된 동전 저장
vector<int> lastUsedCoin(totalAmount + 1, 0);
for (int amount = 1; amount <= totalAmount; ++amount)
{
int minCount = amount; // 최악의 경우 모두 1원짜리 사용
int chosenCoin = 1; // 기본값으로 1원 선택
// 사용 가능한 동전 중에서 최소 동전 수를 만드는 조합 탐색
for (int i = 0; i < coinCount; ++i)
{
if (coins[i] > amount) continue;
int candidate = minCoins[amount - coins[i]] + 1;
if (candidate < minCount)
{
minCount = candidate;
chosenCoin = coins[i];
}
}
minCoins[amount] = minCount;
lastUsedCoin[amount] = chosenCoin;
}
// 결과 출력: 최소 개수 및 사용된 동전 목록
cout << "최소 동전 개수: " << minCoins[totalAmount] << "\n";
cout << "동전 조합: ";
int remaining = totalAmount;
while (remaining > 0)
{
cout << lastUsedCoin[remaining] << " ";
remaining -= lastUsedCoin[remaining];
}
}
int main()
{
cin >> totalAmount; // 금액 입력 받기
tabulation();
return 0;
}
