1. 팩토리얼

• 1부터 n까지 연속한 정수의 곱

  n : 1 x 2 x ... x n-1 x n

1) 반복문 이용

def fact1(n):
	f = 1
    for i in range(1, n+1):
    	f = f * i
    return f

2) 재귀 호출

• 종료 조건 필요

1! = 1
2! = 1 x 2 = 2 x 1!
3! = 1 x 2 x 3 = 3 x 2!
n! = 1 x 2 x ... x (n-1) x n = n x (n-1)!

def fact2(n):
	if n<=1: # 종료 조건
    	return 1
    return n * fact(n-1)

ex) fact2(4)
-> 4! = 4 x 3! = 4 x 3 x 2! = 4 x 3 x 2 x 1! = 4 x 3 x 2 = 4 x 6 = 24

3) 성능

• for문 이용 : 곱셈 n
• 재귀 호출 : 곱셈 n-1

  모두 O(n)

4) 응용

4-1) 1부터 n까지의 합 : 재귀 호출

def sum_n(n):
    if n == 1:
        return 1
    return n + sum_n(n-1)

print(sum_n(3))

4-2) 숫자 n개 중 최댓값 찾기 : 재귀 호출

def find_max(a, n):
    if n == 1:
        return a[0]
    max_n = find_max(a, n-1)

    if max_n > a[n-1]:
        return max_n
    else:
        return a[n-1]
    
    
v = [17, 92, 18, 33, 58, 7, 33, 42]
print(find_max(v, len(v)))

2. 최대 공약수 구하기

• 두 개 이상의 정수 중 가장 큰 약수

1) 반복문

def gcd(a, b):
	i = min(a,b)
    while True:
    	if a % i == 0 and b % i == 0:
        	return i
        i = i - 1

2) 유클리드 알고리즘

• a와 b의 최대공약수는 b와 a%b의 나머지의 최대공약수와 같다
• gcd(a,b) = gcd(b, a%b)
• 어떤 수와 0의 최대공약수는 자기 자신임 -> 종료조건
• gcd(n, 0) = n

ex) gcd(60, 24) = gcd(24, 12) = gcd(12, 0) = 12

def gcd(a,b):
	if b == 0:
    	return a
    return gcd(b, a%b)

3) 피보나치 수열

• 0, 1, 1, 2, 3, 5, 8, 13 ...

def pibo(n):
	if n <= 1:
    	return n

    return pibo(n-1) + pibo(n-2)

3. 하노이의 탑

• 원반이 n개인 하노이의 탑을 옮기기 위한 원반 이동 순서를 출력하는 알고리즘

  • 크기가 다른 원반 n개를 출발 기둥에서 도착 기둥으로 이동
  • 원반은 한 번에 한 개만 이동 가능
  • 원반을 옮길 때는 원반의 맨 위의 것만 이동 가능
  • 큰 원반이 작은 원반 위로 갈 수 없음.

1) 풀이

1-1) 원반이 1개인 경우

• 원반을 기둥 1에서 기둥 3으로 한 번에 옮길 수 있음

1-2) 원반이 2개인 경우

• 1번 기둥의 맨 위 원반을 기둥 2로 옮김
• 1번 기둥의 맨 아래 원반을 기둥 3으로 옮김
• 2번 기둥의 원반을 기둥 3으로 옮김
• 3번만에 원반을 옮김

1-3) 원반이 3개인 경우

• 원반 2개를 기둥 2로 이동(1-2와 같은 원리) : 1->3, 2->2, 1->2
• 1번 기둥에 남아있는 마지막 원반을 기둥 3으로 이동
• 기둥 2의 맨 위 원반을 기둥 1로 이동
• 기둥 2의 원반을 기둥 3으로 이동
• 기둥 1의 원반을 기둥 3으로 이동
• 총 7번만에 원반 이동

1-4) 원반이 n개인 경우

• 1번 기둥의 n-1개의 원반을 2번 기둥으로 이동
• 1번 기둥의 맨 마지막 원반을 3번 기둥으로 이동
• 2번 기둥의 n-1개의 원반을 2번 기둥으로 이동

2) 구현

def hanoi (n, from_pos, to_pos, aux_pos):
    if n ==1:
        print("출발:", from_pos)
        print("->")
        print("도착:", to_pos)
        return
    
    hanoi(n-1, from_pos, aux_pos, to_pos)
    print("출발:", from_pos)
    print("->")
    print("도착:", to_pos)
    hanoi(n-1, aux_pos, to_pos, from_pos)


hanoi(3, 1, 3, 2) 

• hanoi(n-1, from_pos, aux_pos, to_pos) : n-1개 원반을 보조 기둥으로 이동
• hanoi(n-1, aux_pos, to_pos, from_pos) : 보조 기둥에 있는 n-1개의 원반을 목적지 기둥으로 이동.

3) 분석

• 연산횟수 : 2^n - 1

성능 : O(2^n)

4. 재귀 호출을 이용한 그림그리기

• 파이썬 '거북이 그래픽' 이용
• 거북이 그래픽 : 화면 위에 펜 역할을 하는 거북이를 올린 후 거북이가 움직이도록 명령을 내려 그림을 그리게 함

1) 사각 나선 그리기

import turtle as t

def spiral(sp_len):
    if sp_len <= 5:
        return
    t.forward(sp_len)
    t.right(90)
    spiral(sp_len - 5)

t.speed(0)
spiral(200)
t.hideturtle()
t.done()

2) 시에르핀스키의 삼각형 그리기

import turtle as t

def tri(tri_len):
    if tri_len <= 10:
        for i in range(0, 3):
            t.forward(tri_len)
            t.left(120)
        return
    new_len = tri_len / 2
    tri(new_len)
    t.forward(new_len)
    tri(new_len)
    t.backward(new_len)
    t.left(60)
    t.forward(new_len)
    t.right(60)
    tri(new_len)
    t.left(60)
    t.backward(new_len)
    t.right(60)

t.speed(0)
tri(160)
t.hideturtle()
t.done()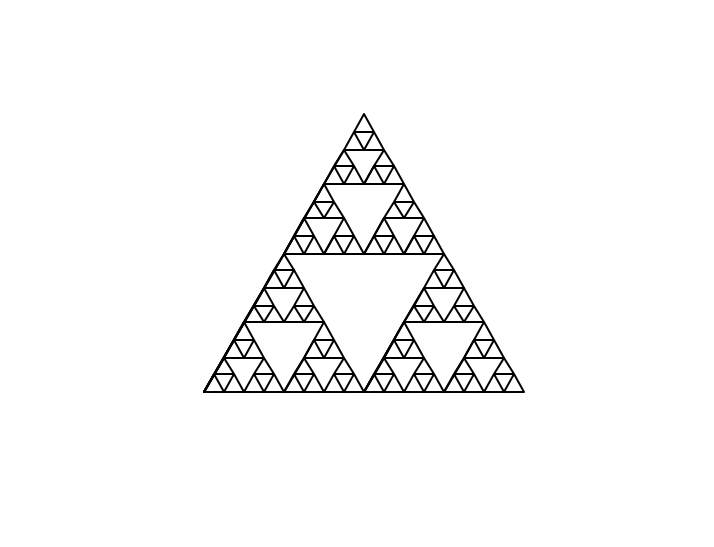

3) 나무 그리기

import turtle as t

def tree(br_len):
    if br_len <= 5:
        return
    new_len = br_len * 0.7
    t.forward(br_len)
    t.right(20)
    tree(new_len)
    t.left(40)
    tree(new_len)
    t.right(20)
    t.backward(br_len)

t.speed(0)
t.left(90)
tree(70)
t.hideturtle()
t.done()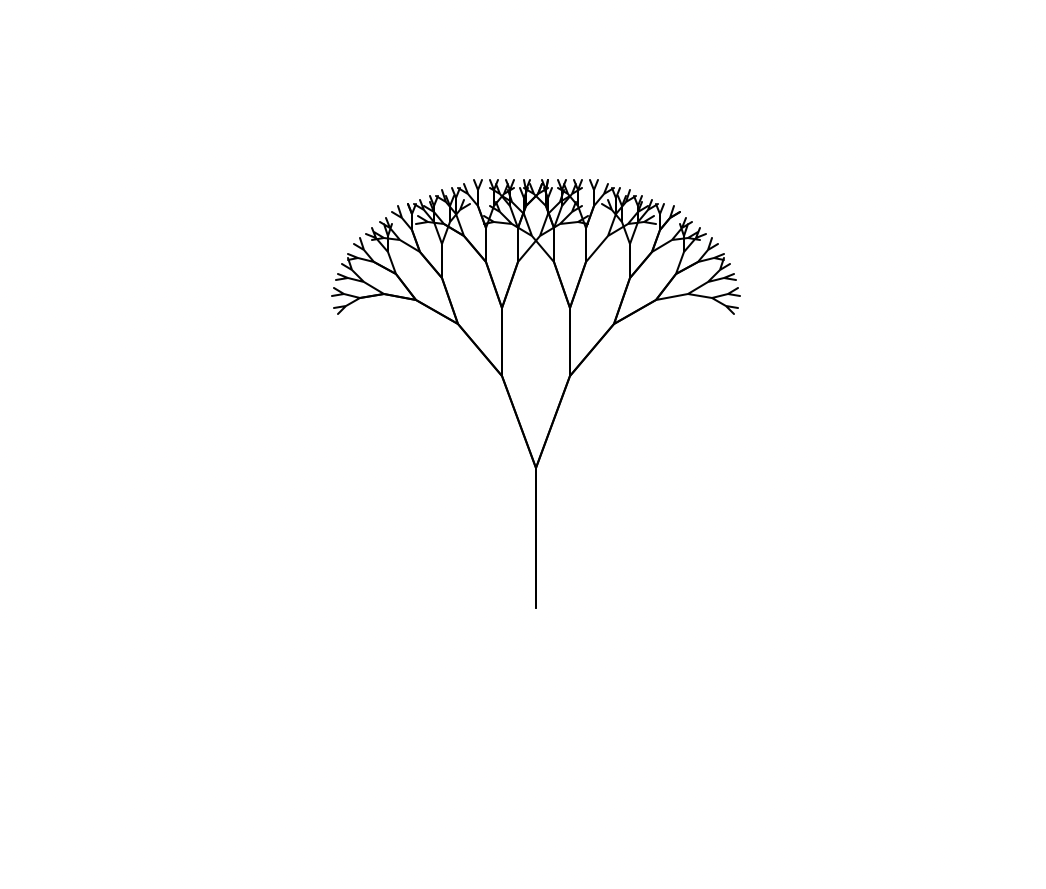

4) 눈꽃 그리기

import turtle as t

def snow(snow_len):
    if snow_len <= 10:
        t.forward(snow_len)
        return
    new_len = snow_len / 3
    snow(new_len)
    t.left(60)
    snow(new_len)
    t.right(120)
    snow(new_len)
    t.left(60)
    snow(new_len)

t.speed(0)
snow(150)
t.right(120)
snow(150)
t.right(120)
snow(150)
t.hideturtle()
t.done()