7.1.용어

1) 노드

• 그래프의 정점과 비슷
• root 노드 : 맨 위의 노드
• 부모, 자식 노드 : 1단계 차이
• 조상, 자손 노드 : 2단계 차이

2) 차수

• 어떤 노드의 자식 노드 개수
• 트리의 차수(degree of a tree) : 트리에 있는 노드의 최대 차수
• 리프 노드(leaf node) : 자식이 없는 노드
• 내부 노드 (internal node) : 루트 노드, 리프노드를 제외한 트리 내 모든 노드

3) 레벨

• 루트의 레벨을 레벨 1로 하고 자식으로 내려가면서 하나씩 더해지는 개념

• 깊이와 연관되어 있음

• 트리의 깊이(depth)/높이(height) : 트리가 가지는 최대 레벨

  e = n - 1
  -> e >= n이 되는 경우, 트리에서는 사이클이 생겨서 더이상 트리가 아니게 됨.

• e : 에지의 개수, n : 노드의 개수

4) 이진 트리(binary tree)

트리를 구성하는 노드의 자식이 최대 2개인 트리

• 레벨 l에 대한 이진 트리의 최대 노드의 개수 : 2^ㅣ-1
• 트리 높이 h에 대한 이진트리의 최대 노드의 개수 : 2^h - 1

4-1) 포화 이진트리(full binary tree)

• 트리 높이 h에 대한 이진트리의 최대 노드의 개수가 2^h - 1 인 트리

4-2) 완전 이진트리(complete binary tree)

• 높이 h일 때, h-1까지의 노드 개수가 2^h-1 - 1이고, 높이 h에서는 노드가 왼쪽에서 오른쪽으로 채워지는 트리

4-3) 편향 이진트리(skewed binary tree)

• 왼쪽이나 오른쪽 서브트리만 가진 이진 트리

7.2. 이진트리의 순회 : 모든 노드 방문

1) 전위 순회(preorder traversal)

• 방문순서 : 현재노드 > 왼쪽 서브트리 > 오른쪽 서브트리

1-1) 재귀적으로 방문 수행

• 왼쪽 서브트리의 서브트리까지 모두 탐색 후에 오른쪽 서브트리로 넘어가기 때문

class Node:
    def __init__(self, item):
        self.item = item
        self.left = None
        self.right = None

class BinaryTree():
    def __init__(self):
        self.root = None
    
    def preorder(self, n):
        if n!= None:
            print(n.item, '', end='')
            if n.left:
                self.preorder(n.left)
            if n.right:
                self.preorder(n.right)


tree = BinaryTree()
n1 = Node(1)
n2 = Node(2)
n3 = Node(3)
n4 = Node(4)
n5 = Node(5)
n6 = Node(6)
n7 = Node(7)

tree.root = n1
n1.left = n2; n1.right = n3
n2.left = n4; n2.right = n5
n3.left = n6; n3.right = n7
# 트리 만들기

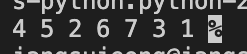
print(tree.preorder(tree.root))

1-2) 스택과 반복문 이용

def iter_preorder(cur):
        s = Stack()
        while True:
            while cur:
                print(cur.data, end='')
                s.push(cur)
                cur = cur.left
            cur = s.pop()
            if not cur :
                break
            cur = cur.right 

• cur = cur.left : 왼쪽 방향으로 쭉 순회
• cur = s.pop() : pop을 통해 가져온 노드
  1) None : 스택이 비어 있는 경우, 즉 모든 노드를 순회한 경우
  2) 왼쪽 서브트리가 빔
  3) 왼쪽 서브트리를 방문한 상태
• cur = cur.right : 왼쪽 서브트리를 방문했으므로 오른쪽 서브트리 방문할 차례

2) 중위 순회(inorder traversal)

• 방문 순서 : 왼쪽 서브트리 -> 현재노드 -> 오른쪽 서브트리

• 왼쪽 서브트리의 최하위층에서부터 시작함.

2-1) 재귀 이용

def inorder(self, n):
        if n == None:
            return    
        self.inorder(n.left)
        print(n.item, '', end='')
        self.inorder(n.right)

2-2) 스택과 반복문 이용

def iter_inorder(cur):
    s = Stack()
    while True:
        while cur:
            s.push(cur)
            cur = cur.left
        cur = s.pop()
        if not cur:
            break
        # pop한 후에 방문을 합니다.
        print(cur.data, end=' ')
        cur = cur.right

3) 후위 순회(postorder traversal)

방문순서 : 왼쪽 서브트리 -> 오른쪽 서브트리 -> 현재 노드

def postorder(self, n):
        if n!=None:
            if n.left:
                self.postorder(n.left)
            if n.right:
                self.postorder(n.right)
            print(n.item, '', end='')

4) 레벨 순서 순회(levelorder traversal)

• 큐를 사용하여 순회

  레벨을 하나씩 내려가면서 해당 레벨에 있는 모든 노드 순회

def levelorder(self, root):
        q = Queue()
        q.put(root)

        while not q.empty():
            t = q.get()
            print(t.item, end=' ')

            if t.left:
                q.put(t.left)
            if t.right:
                q.put(t.right)

• 해당 노드의 자식노드가 존재한다면, 해당 노드를 큐에 넣음.
• adj[cur] = {cur.left, cur.right}
• 큐가 빌 때까지 반복하면 깊이가 깊어짐 -> 모든 노드 방문