9.1. 이진 탐색 트리의 문제점
- 데이터가 정렬된 상태에서 들어오면 각 레벨마다 노드를 하나씩만 가져 결국은 연결리스트 구조가 됨.
- 해결 : 회전(rotation)을 이용
9.2. 레드 블랙 트리
1) 확장 이진 트리(extended binary tree)
- 모든 빈 노드를 외부 노드(external node)로 대체함
- 이전 리프 노드가 더이상 리프노드가 아니게 됨
- 내부 노드(internal node) : 리프노드를 제외한 모든 노드
2) 레드 블랙 트리
모든 노드의 컬러가 블랙 혹은 레드인 이진 탐색 트리
- 블랙 : 루트, 외부 노드
- 특징
- 트리의 모든 노드는 블랙 아니면 레드
- 루트 노드와 외부 노드 : 블랙
- 루트 노드에서 외부 노드까지 경로에서 레드 노드가 연속으로 나올 수 없음
: 부모 노드가 레드면, 자식 노드는 무조건 블랙 -> 레드 규칙(insert 연산) - 루트 노드에서 외부 노드까지 모든 경로에서 블랙 노드 개수는 같음
: delete 연산으로 인해 블랙 노드가 삭제되는 경우
- 회전
- 왼쪽 회전 : 노드 r을 축으로 노드 n을 왼쪽, 즉 반시계 방향으로 회전하는 것. r의 왼쪽 자식이었던 내부 노드 혹은 외부 노드 l을 노드 n의 오른쪽 자식으로 만들어 주어야 함.
- 오른쪽 회전 : 노드 l을 축으로 노드 n을 오른쪽, 즉 시계 방향으로 회전. 노드 l의 오른쪽 자식인 내부 노드 혹은 외부 노드 r을 노드 n의 왼쪽 자식으로 만들어 주는 것
-삽입 연산
- BST 삽입 연산과 같음 : 새로 삽입된 노드는 RED
- 삽입된 노드와 부모노드가 모두 RED인 경우, 레드 규칙 위반 > insert_fix로 다룸
- insert_fix
1) 루트 노드 : red 인 경우, black으로 변경함.
2) 레드 규칙 위반을 8가지 경우로 나누어서 다룸 :
2-1. 조부모 노드의 왼쪽 자식 노드가 새 노드의 부모 노드인 경우
- n : 새로 삽입된 노드, red
- p : n의 부모노드, g의 왼쪽 노드, red
- g : p의 부모노드, n의 조부모 노드로 black
- u : p의 형제노드, g의 오른쪽 노드
- 경우의 수
1) LLr : n이 p의 왼쪽 노드이며, u의 색상 red
-> 1. 조부모의 색을 red로 변경(g)
-> 2. 부모와 부모 형제 노드 색을 black으로 변경(u,p)
-> 경로상 black 노드 개수 : 1
-> 3. 노드 n을 조부모 g로 이동하여 그의 부모(새로운 p)가 black이면 종료, red면 반복 실행
-> 4. 계속 타고 올라가다가 root가 red가 되는 경우에는 root를 black으로 변경 후 알고리즘 종료.
2) LRr : n이 p의 오른쪽 노드, u의 색상 red
3) LLb : n이 p의 왼쪽 노드, u : black
4) LRb : n이 p의 오른쪽 노드, u : black
-> 1. 부모노드 p에 대하여 왼쪽 회전 : LLb로 만들어줌
-> 2. p를 black, g를 red로 바꿈
-> 3. g 기준 오른쪽 회전
2-2. 조부모 노드의 오른쪽 자식 노드가 새 노드의 부모 노드인 경우
- n : 새로 삽입된 노드, red
- p : n의 부모노드, g의 오른쪽 노드, red
- g : p의 부모노드, n의 조부모 노드로 black
- u : p의 형제노드, g의 왼쪽 노드
- 경우의 수
1) RLr : n이 p의 왼쪽 노드이며, u의 색상 red
2) RRr : n이 p의 오른쪽 노드, u의 색상 red
3) RLb : n이 p의 왼쪽 노드, u : black
4) RRb : n이 p의 오른쪽 노드, u : black
3) 구현
- 모든 빈 노드가 하나의 외부 노드를 가리키게 만들어서 리프노드, 자식이 하나인 노드의 외부 노드 역할을 수행하게 함.
class RBNode:
def __init__(self, key) :
self.key = key
self.color = "RED"
self.left = None
self.right = None
self.parent = None
def __str__(self):
return str(self.key)- 이진 트리 구현한 노드에서 color 값만 추가됨
class RedBlackTree:
def __init__(self):
self.__root = None
self.__EXT = RBNode(None)
self.__EXT.color = "BLACK"
def get_root(self):
return self.__root
def preorder_traverse(self, cur, func, *args, **kwargs):
if cur == self.__EXT:
return
func(cur, *args, **kwargs)
self.preorder_traverse(cur.left, func, *args, **kwargs)
self.preorder_traverse(cur.right, func, *args, **kwargs)
- __EXT 라는 멤버를 두어 RBNode 인스턴스 하나를 참조하게 함
- 외부 노드이므로 black
def __left_rotate(self, n):
r = n.right #n의 오른쪽 자식
l = r.left #r의 왼쪽 자식
l.parent = n
n.right = l
#l을 n의 오른쪽 자식으로
if n == self.__root:
self.__root = r
elif n.parent.left == n:
n.parent.left = r
else:
n.parent.right = r
r.parent = n.parent
r.left = n
n.parent = r
#n을 r의 왼쪽 자식으로
def __right_rotate(self, n):
l = n.left
r = l.right
r.parent = n
n.left = r
if n == self.__root:
self.__root = r
elif n.parent.left == n:
n.parent.left = l
else:
n.parent.right = l
l.parent = n.parent
l.right = n
n.parent = l- 왼쪽 / 오른쪽 회전
def insert(self, key):
new_node = RBNode(key)
new_node.left=self.__EXT
new_node.right=self.__EXT
cur = self.__root
if not cur:
self.__root = new_node
self.__root.color = "BLACK"
return
while True:
parent = cur
if key < cur.key:
parent.left = new_node
new_node.parent = parent
break
else:
cur = cur.right
if cur == self.__EXT:
parent.right = new_node
new_node.parent = parent
break
self.__insert_fix(new_node)- insert 연산 : while 문 이후 insert_fix 연산 수행하여 노드의 재배치 수행
def __insert_fix(self, n):
pn = gn = un = None
pn = n.parent
while pn != None and pn.color == "RED":
gn = pn.parent
if gn.left == pn:
un = gn.right
if un.color == "RED":
gn.color = "RED"
pn.color = un.color = "BLACK"
n = gn
pn = n.parent
else:
if pn.right == n:
self.__left_rotate(pn)
n, pn = pn, n
pn.color, gn.color = gn.color, pn.color
self.__right_rotate(gn)
else:
un = gn.left
if un.color == "RED":
gn.color = "RED"
pn.color = un.color = "BLACK"
n = gn
pn = n.parent
else:
if pn.left == n:
self.__right_rotate(pn)
n, pn = pn, n
pn.color, gn.color = gn.color, pn.color
self.__left_rotate(gn)
self.__root.color = "BLACK" - pn : n의 부모
- gn : n의 조부모
- un : pn의 형제
while pn != None and pn.color == "RED":: n이 root가 아니고, n의 부모 색상이 redgn = pn.parent: pn이 red면, 반드시 gn 존재. 루트는 black이므로 gn은 root가 아님.if gn.left == pn:: pn이 gn의 왼쪽 자식인 경우if un.color == "RED":: 부모의 형제가 redgn.color = "RED"; pn.color = un.color = "BLACK": 부모, 부모형제, 조부모의 색 변경n = gn: gn을 새로운 n으로 만든 후, 연속된 레드가 일어나는지 확인else:: 부모 형제가 black인 경우if pn.right == n:: LRbpn.color, gn.color = gn.color, pn.color: LLb 라면 부모와 조부모의 색상 바꿈else:: pn이 gn의 오른쪽 자식인 경우un = gn.left: 조부모의 왼쪽 자식이 외부 노드라면 부모 형제를 en으로 변경
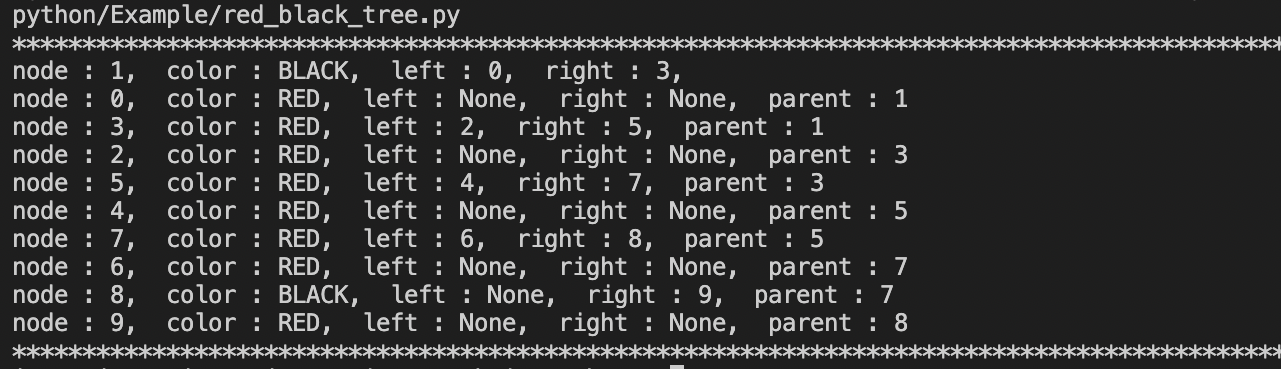
def print_node(self, rbn):
if rbn:
print("node : {}, ".format(rbn.key), end=" ")
if rbn.color == "RED":
print("color : RED, ", end=" ")
else:
print("color : BLACK, ", end=" ")
if rbn.left:
print("left : {}, ".format(rbn.left.key), end=" ")
if rbn.right:
print("right : {}, ".format(rbn.right.key), end=" ")
if rbn.parent:
print("parent : {}".format(rbn.parent.key), end=" ")
print()
if __name__ == "__main__":
print('*'*100)
rbt = RedBlackTree()
for i in range(10):
rbt.insert(i)
rbt.preorder_traverse(rbt.get_root(), rbt.print_node)
print('*'*100) def print_node(self, rbn):
if rbn:
print("node : {}, ".format(rbn.key), end=" ")
if rbn.color == "RED":
print("color : RED, ", end=" ")
else:
print("color : BLACK, ", end=" ")
if rbn.left:
print("left : {}, ".format(rbn.left.key), end=" ")
if rbn.right:
print("right : {}, ".format(rbn.right.key), end=" ")
if rbn.parent:
print("parent : {}".format(rbn.parent.key), end=" ")
print()
if __name__ == "__main__":
print('*'*100)
rbt = RedBlackTree()
for i in range(10):
rbt.insert(i)
rbt.preorder_traverse(rbt.get_root(), rbt.print_node)
print('*'*100)