op - Supply Chain Management

SCM : 용량제약 입지선정모형

1. SCM : 모델링

2. SCM : 기본 코드

from ortools.linear_solver import pywraplp
solver = pywraplp.Solver.CreateSolver("SCIP")
infinity = solver.infinity()
BIGM = 100000000

# 비용
DATA = [[1675, 400, 685, 1630, 1160, 2800],
        [1460, 1940, 970, 100, 495, 1200],
        [1925, 2400, 1425, 500, 950, 800],
        [380, 1355, 543, 1045, 665, 2321],
        [922, 1646, 700, 508, 311, 1797]]

# 수요량
a = [10, 8, 12, 6, 7, 11]

# 공급량
b = [18, 24, 27, 22, 31]

# 고정비
f = [7650, 3500, 3500, 4100, 2200]

# 의사결정변수(x[1,1]은 창고 a에서 수요도시1로의 배송량 / y는 창고 가동여부 이진변수 가동하면 1 가동하지 않으면 0)
x = {}
for i in range(5):
    for j in range(6):
        x[i,j] = solver.IntVar(0, infinity, f"x[{i},{j}]")
    
y = {}
for i in range(5):
    y[i] = solver.IntVar(0, 1, "y[%i]" % i)


# 고정비용관련 제약조건
for i in range(5):
    for j in range(6):
        solver.Add(x[i,j]<= BIGM*y[i])

# 수요 제약조건 
for j in range(6):
    solver.Add(sum([x[i,j] for i in range(5)])>= a[j])

# 공급 제약조건
for i in range(5):
    solver.Add(sum([x[i,j] for j in range(6)]) <= b[i])



# 목적함수 : 비용최소화
expr = [] # 변동비
for i in range(5):
    for j in range(6):
        expr.append(DATA[i][j]*x[i,j])

expr_f = [] # 고정비
for i in range(5):
    expr_f.append(f[i]*y[i])


solver.Minimize(sum(expr) + sum(expr_f))


with open('예제1', "w") as out_f:
    lp_text = solver.ExportModelAsLpFormat(False)
    out_f.write(lp_text)

status = solver.Solve()

if status == pywraplp.Solver.OPTIMAL:
    print("OPTIMAL")
    print("목적함수값 = %.1f" % solver.Objective().Value())
    for i in range(5):
        for j in range(6):
            print(x[i,j].name(), " = ", x[i,j].solution_value())
    for i in range(5):
        print(y[i].name(), " = ", y[i].solution_value())
else:
    print("The problem does not have an optimal solution.")

3. SCM : 관련 문제

세계적인 PC 제조업체인 델컴퓨터는 비용을 줄이기 위한 방안으로 유럽생산기지를 루마니아, 폴란드, 아일랜드 중 하나로 옮기고자 한다. 수요 시장별 연간 예상 수요량, 각 입지 후보지별 생산능력 및 시설 고정비용, 생산 후보지로 부터 각 수요시장으로 연간 분배비용(생산, 재고, 수송을 포함한 비용)은 다음표와 같다.

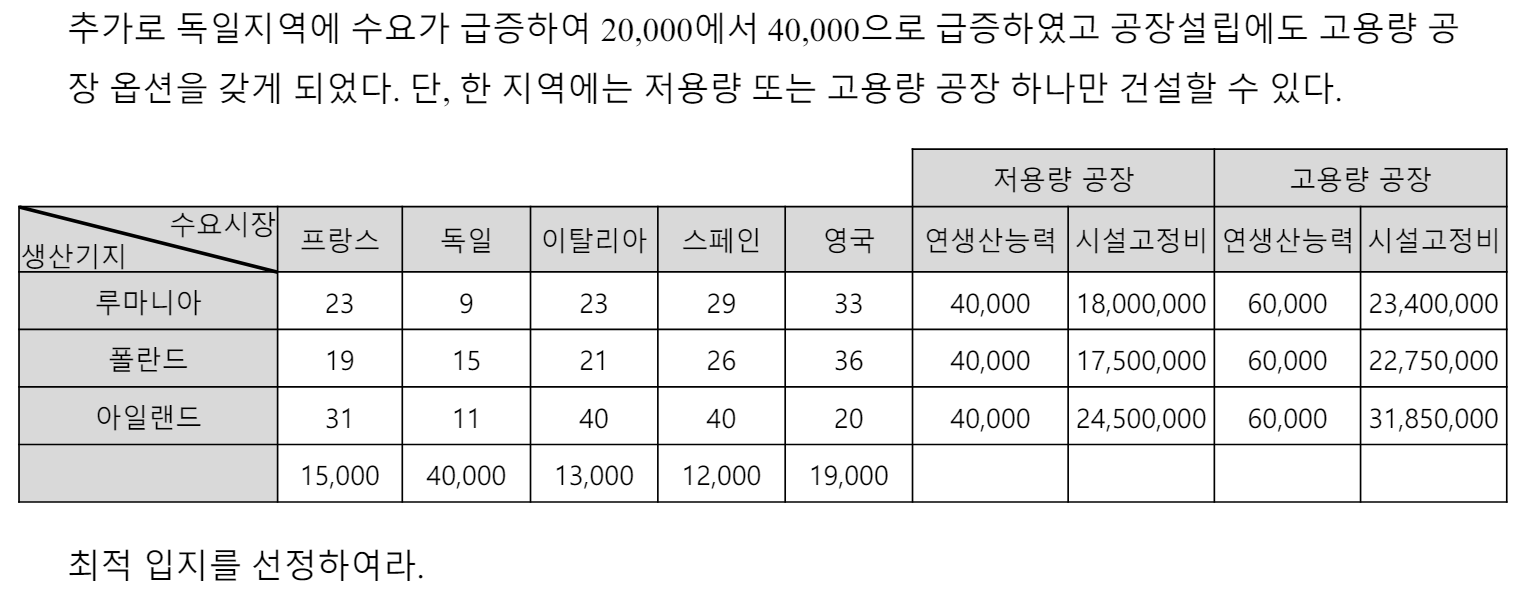
# 저생산 / 고생산 모두 고려해서 풀이 
from ortools.linear_solver import pywraplp
solver = pywraplp.Solver.CreateSolver("SCIP")
infinity = solver.infinity()
BIGM = 100000000

# 비용
DATA = [[23, 9, 23, 29, 33],
        [19, 15, 21, 26, 36],
        [31, 11, 40, 40, 20]]

# 수요량
a = [15000, 40000, 13000, 12000, 19000]


# 저 생산공장
low_f = [18000000, 17500000, 24500000] # 고정비
low_b = [40000, 40000, 40000] # 공급능력

# 고 생산공장
high_f = [23400000, 22750000, 31850000] # 고정비
high_b = [60000, 60000, 60000] # 공급능력



# 의사결정변수(x[1,1]은 창고 a에서 수요도시1로의 배송량 / y는 저 생산공장 가동여부 이진변수 가동하면 1 가동하지 않으면 0 / z는 고 생산공장 가동여부 이진변수)
x = {}
for i in range(3):
    for j in range(5):
        x[i,j] = solver.IntVar(0, infinity, f"x[{i},{j}]")
    
y = {}
for i in range(3):
    y[i] = solver.IntVar(0, 1, "y[%i]" % i)

z = {}
for i in range(3):
    z[i] = solver.IntVar(0, 1, "z[%i]" % i)


# 공장 건설공장 : 저생산 or 고생산 중에서 최대 1개 생산가능함
for i in range(3):
    solver.Add(y[i] + z[i] <= 1)


# 고정비용관련 제약조건
for i in range(3):
    for j in range(5):
        solver.Add(x[i,j]<= BIGM*y[i] + BIGM*z[i])


# 수요 제약조건 
for j in range(5):
    solver.Add(sum([x[i,j] for i in range(3)])>= a[j])


# 공급 제약조건
for i in range(3):
    solver.Add(sum([x[i,j] for j in range(5)]) <= (low_b[i]*y[i] + high_b[i]*z[i]))



# 목적함수 : 비용최소화
expr = [] # 변동비
for i in range(3):
    for j in range(5):
        expr.append(DATA[i][j]*x[i,j])

expr_f = [] # 고정비
for i in range(3):
    expr_f.append(low_f[i]*y[i] + high_f[i]*z[i])


solver.Minimize(sum(expr) + sum(expr_f))


with open('연습문제2-2', "w") as out_f:
    lp_text = solver.ExportModelAsLpFormat(False)
    out_f.write(lp_text)

status = solver.Solve()

if status == pywraplp.Solver.OPTIMAL:
    print("OPTIMAL")
    print("목적함수값 = %.1f" % solver.Objective().Value())
    for i in range(3):
        for j in range(5):
            print(x[i,j].name(), " = ", x[i,j].solution_value())
    for i in range(3):
        print(y[i].name(), " = ", y[i].solution_value())
    for i in range(3):
        print(z[i].name(), " = ", z[i].solution_value())
else:
    print("The problem does not have an optimal solution.")

최단 경로 문제

1. 최단 경로 : 모델링

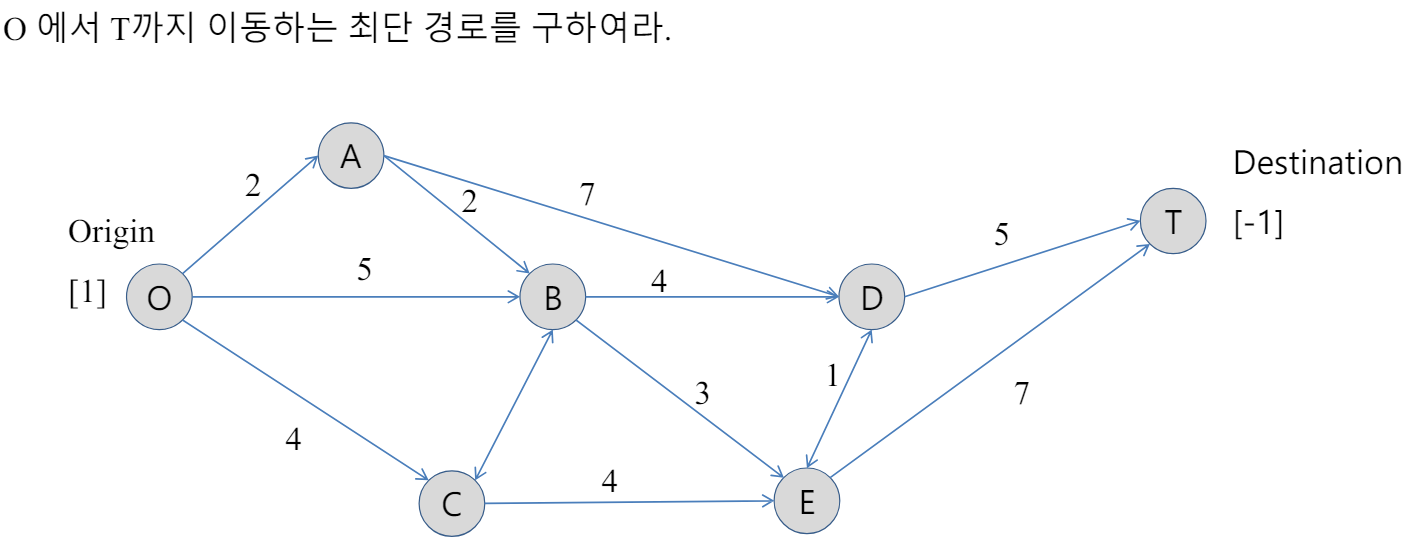
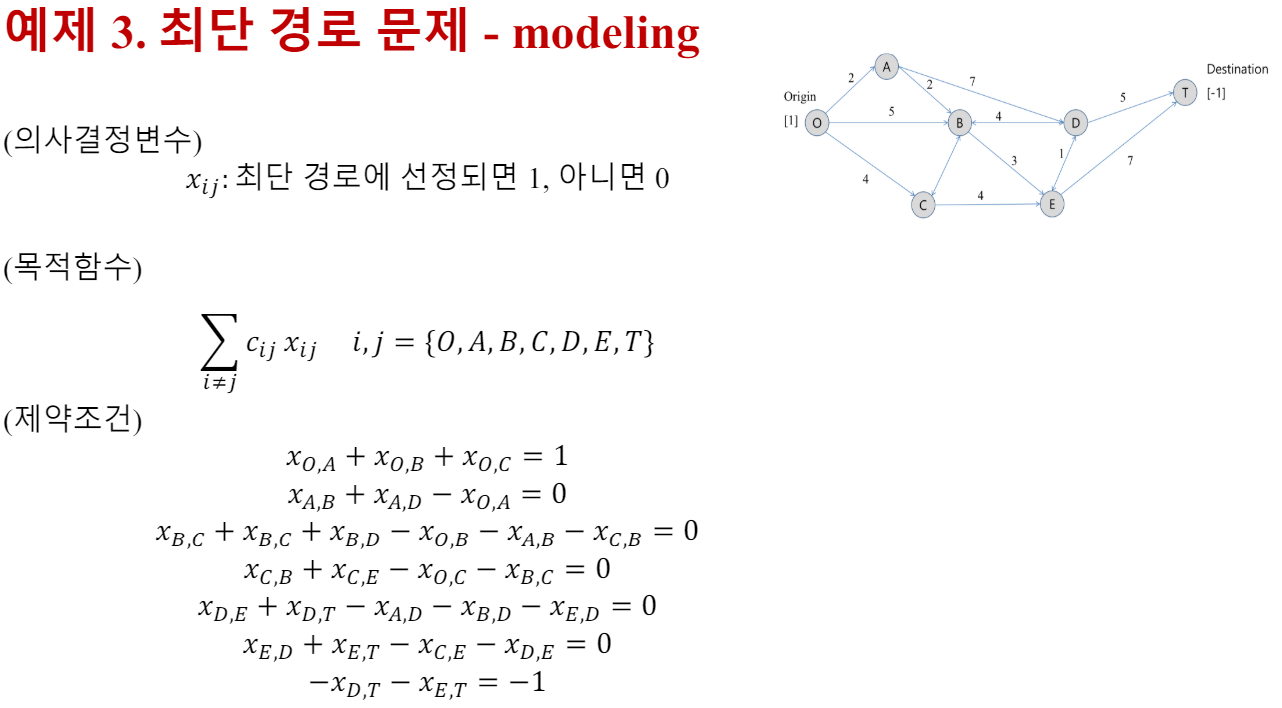
2. 최단 경로 : 기본 예제

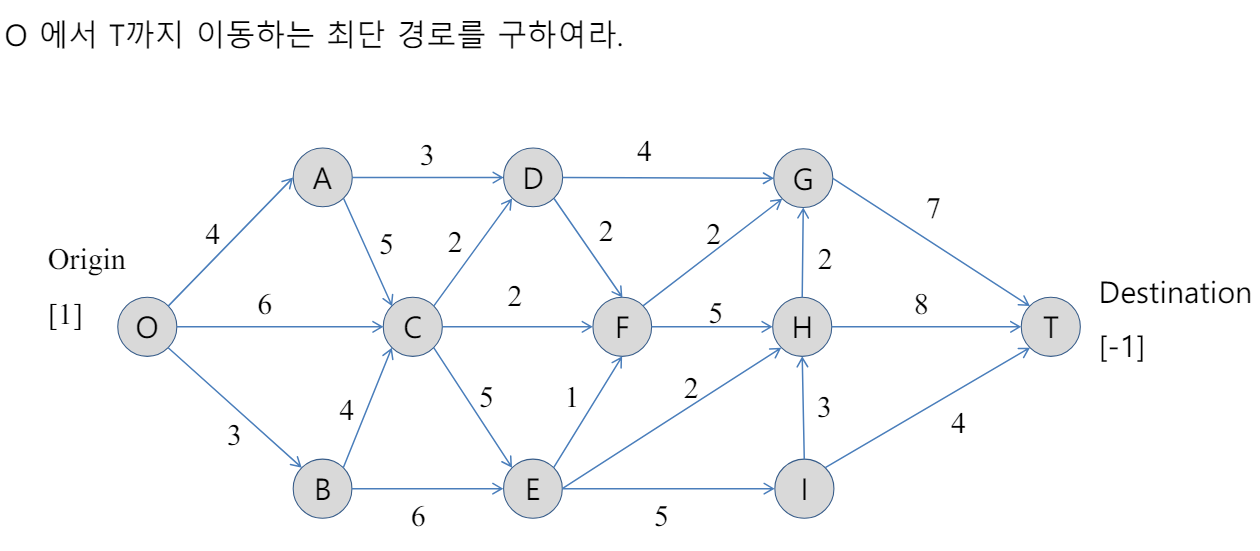
# 풀이
from ortools.linear_solver import pywraplp
solver = pywraplp.Solver.CreateSolver("SCIP")
infinity = solver.infinity()

# 각 node의 명칭을 붙이고 딕셔너리형태로 저장
node_name = {0: 'O', 1: 'A', 2: 'B', 3: 'C', 4: 'D', 5: 'E', 6: 'F', 7: 'G', 8 : 'H', 9 : 'I', 10 : 'T'}

COSTS = {(0, 1): 4, (0, 2) : 3, (0, 3): 6, 
(1, 3): 5, (1, 4): 3,
(2, 3): 4, (2, 6): 6, 
(3, 4): 2, (3, 5): 5, (3, 6): 2,
(4, 6): 2, (4, 7): 4,
(5, 6): 1, (5, 8): 2, (5,9) : 5,
(6,7): 2, (6,8) : 5, 
(7,10) : 7,
(8,7) : 2, (8,10) : 8,
(9,8) : 3, (9,10): 4}

FLOW = [1, 0, 0, 0, 0, 0, 0, 0, 0, 0 -1]

nNodes = len(FLOW)

x = {}
for key in COSTS.keys():
    x[key] = solver.IntVar(0, 1, "X[%i,%i]" %(key[0], key[1]))

# 제약조건
for i in range(nNodes):
    const_expr = []
    for key in COSTS.keys():
        if key[0] == i: # incoming traffic
            const_expr.append(x[key])
        elif key[1] == i: # outgoing traffic
            const_expr.append(-x[key[0], key[1]])
    
    solver.Add(solver.Sum(const_expr) == FLOW[i], 'node_'+str(i))

    
obj_expr = []
for key in COSTS.keys():
    obj_expr.append(COSTS[key] * x[key])
    


solver.Minimize(sum(obj_expr))


with open("연습문제3", "w") as out_f:
    lp_text = solver.ExportModelAsLpFormat(False)
    out_f.write(lp_text)

status = solver.Solve()

if status == pywraplp.Solver.OPTIMAL:
    print("OPTIMAL")
    print("목적함수값 = %.1f" % solver.Objective().Value())
    for i in COSTS.keys():
        print(x[i].name(), " = ", x[i].solution_value())
else:
    print("The problem does not have an optimal solution.")