op- 선형모델링

선형계획법(Linear Programming)

1. 선형모델링 문제(기본)

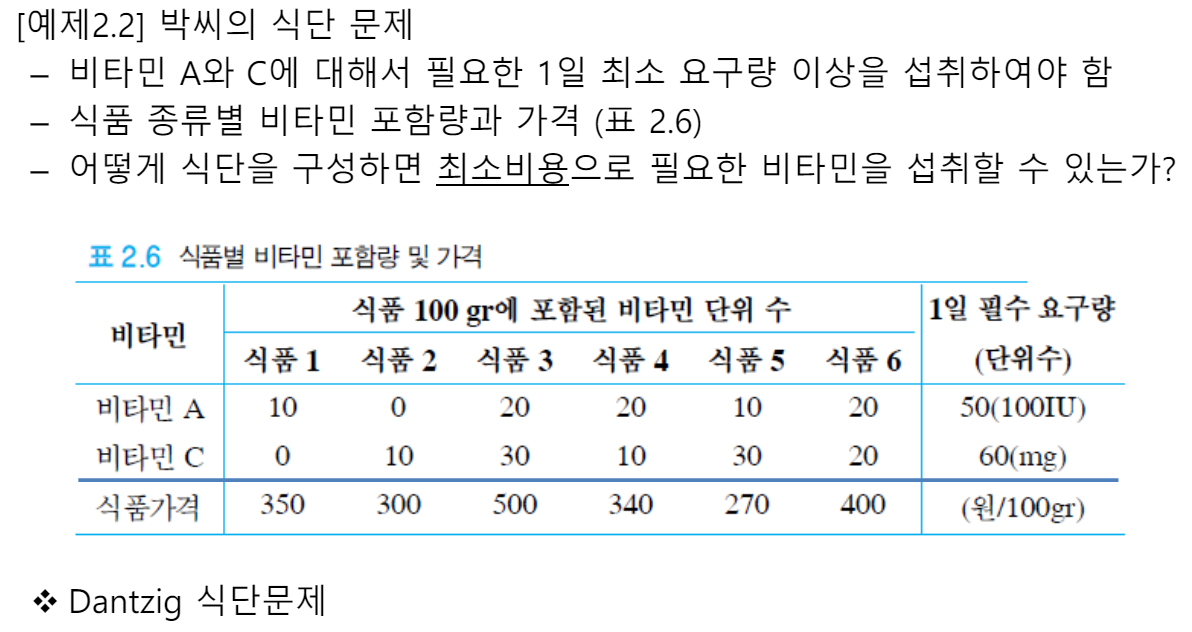
1. 비타민 섭취문제

from ortools.linear_solver import pywraplp
solver = pywraplp.Solver.CreateSolver("SCIP")

# 의사결정 변수생성을 위한 준비작업

data = {}
data["constraint_coeffs"] = [
[10, 0, 20, 20, 10, 20],
[0, 10, 30, 10, 30, 20]
]
data["supply"] = [50, 60]
data["prices"] = [350, 300, 500, 340, 270, 400]
data["num_vars"] = 6
data["num_constraints"] = 2

# 의사결정 변수생성(for문을 활용하여 간편하게 생성)
x = {}
for j in range(data["num_vars"]):
    x[j] = solver.NumVar(0, solver.infinity(), "식품[%i]" % j)

# 제약식(for문을 이용함 / 비타민a와 비타민 c의 1일 필수요구량보다 크거나 같다로 설정함)
for i in range(data['num_constraints']):
    constraint_expr = [data['constraint_coeffs'][i][j] * x[j] for j in range(data['num_vars'])]
    solver.Add(solver.Sum(constraint_expr)>= data['supply'][i])

# 목적함수(식품 1~6별 가격과 구매량을 곱한것의 최솟값이 목적함수임)
objective = solver.Objective()
obj_expr = [data['prices'][j] * x[j] for j in range(data['num_vars'])]

solver.Minimize(solver.Sum(obj_expr))

print(f"Solving with {solver.SolverVersion()}")

status = solver.Solve()

if status == pywraplp.Solver.OPTIMAL:
    print("Objective value =", solver.Objective().Value())
    for j in range(data["num_vars"]):
        print(x[j].name(), " = ", x[j].solution_value())
else:
    print("The problem does not have an optimal solution.")

2. 데이터 가져와서 사용하기

from or2_4_data import *

2. 선형모델링(고급)

1. 기계 scheduling (Bazarra 교재)

from ortools.linear_solver import pywraplp
solver = pywraplp.Solver.CreateSolver("SCIP")
infinity = solver.infinity()

p_names = ['Small', 'Medium', 'Large', 'ExLarge']
m_names = ['A', 'B', 'C']
o_costs = [30, 50, 80]
demands = [10000, 8000, 6000, 6000]
p_rates = [
[300, 600, 800],
[250, 400, 700],
[200, 350, 600],
[100, 200, 300]
]

# 의사결정 변수 : i = 0(Small), 1(Medium), 2(Large), 3(Ex Large) / j = 0(A), 1(B), 2(C)
X = {}
for i in range(len(p_names)):
    for j in range(len(m_names)):
        X[i, j] = solver.NumVar(0, infinity, "X"+str(i)+str(j))

const_expr = []

# 제약조건 : 생산요구량
for i in range(len(p_names)):
    solver.Add(sum([p_rates[i][j]*X[i,j] for j in range(len(m_names))])>= demands[i], p_names[i]+'_demand')
    
# 제약조건 : 기계시간제약
for j in range(len(m_names)):
    solver.Add(sum([X[i,j] for i in range(len(p_names))]) <= 50, m_names[j]+'_capa')

# 목적함수 : 최소화
obj_expr = [o_costs[j] * X[i, j] for i in range(len(p_names)) for j in range(len(m_names))]

solver.Minimize(solver.Sum(obj_expr))

# 모델 파일 생성
with open('or3-1.lp', "w") as out_f:
    lp_text = solver.ExportModelAsLpFormat(False)
    out_f.write(lp_text)

status = solver.Solve()

if status == pywraplp.Solver.OPTIMAL:
    print("Objective value = %.1f" % solver.Objective().Value())
    for i in range(len(p_names)):
        for j in range(len(m_names)):
            print(p_names[i], '/', m_names[j], ': ', \
            X[i, j].name(), " = %.1f" % X[i, j].solution_value())
else:
    print("The problem does not have an optimal solution.")

2. 투자문제 : 초기투자 2200불 (Bazarra 교재)

from ortools.linear_solver import pywraplp
solver = pywraplp.Solver.CreateSolver("SCIP")
inity = solver.infinity()

#의사결정 변수
x = {} # 1년 적금 투자 금액
for i in range(5):
    x[i] = solver.NumVar(0, infinity, "x[%i]" % i)

y = {} # 2년 적금 투자 금액
for i in range(4):
    y[i] = solver.NumVar(0, infinity, "y[%i]" % i)

z = {} # 3년 적금 투자 금액
for i in range(1,3):
    z[i] = solver.NumVar(0, infinity, "z[%i]" % i)

s = {} # 투자후 남은 잔액
for i in range(5):
    s[i] = solver.NumVar(0,infinity,"s[%i]"%i)


# 제약식
solver.Add(x[0] + y[0] + s[0] == 2200, 'year 1')
solver.Add(x[1] + y[1] + z[1] + s[1] == 1.08*x[0] + s[0], 'year 2')
solver.Add(x[2] + y[2] + z[2] + s[2] == 1.08*x[1] + 1.17*y[0] + s[1], 'year 3')
solver.Add(x[3] + y[3] + s[3]== 1.08*x[2] + 1.17*y[1] + s[2], 'year 4')
solver.Add(x[4] + s[4] == 1.08*x[3] + 1.17*y[2] + 1.27*z[1] + s[3], 'year 5')           
           

# 목적함수 : 최대화
objective = solver.Objective()
solver.Maximize(1.17*y[3] + 1.27*z[2] + 1.08*x[4] + s[4])

with open('or3-2.lp', "w") as out_f:
    lp_text = solver.ExportModelAsLpFormat(False)
    out_f.write(lp_text)

status = solver.Solve()

if status == pywraplp.Solver.OPTIMAL:
    print("Objective value =", solver.Objective().Value())
    for i in range(5):
        print(x[i].name(), " = ", x[i].solution_value())
    for i in range(4):
        print(y[i].name(), " = ", y[i].solution_value())
    for i in range(1,3):
        print(z[i].name(), " = ", z[i].solution_value())
    for i in range(5):
        print(s[i].name(), "=", s[i].solution_value())
else:
    print("The problem does not have an optimal solution.")