백준_1991_트리순회
https://www.acmicpc.net/problem/1991
문제를 만나고... 과거에 분명 했었던 것 같은 이진트리가 생각이 나지않아 이번엔 까먹지 않게 확실히 정리하자..!
라는 마음으로 이진트리에 대해 정리하는 글 _〆(。。)
🤷♂️ 이진트리?
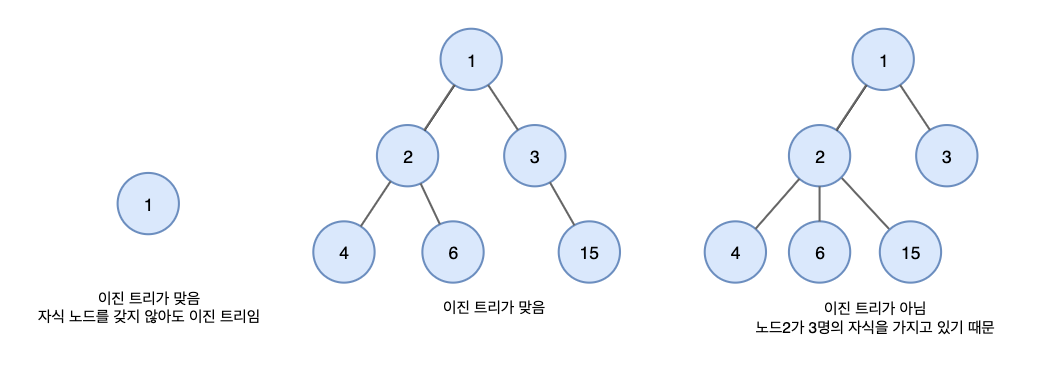
모든 노드들이 둘 이하(0,1,2 개)의 자식을 가진 트리.
❗️ 자식노드의 위치가 각각 왼쪽과 오른쪽으로 다르다면 서로 다른 트리!
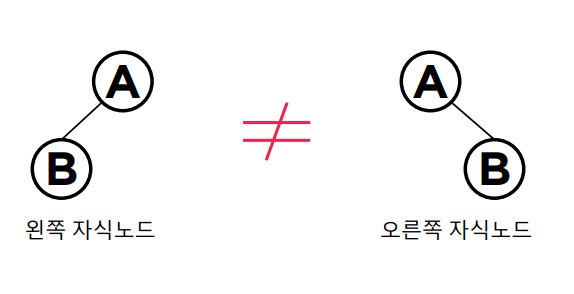
🙆♂️ 이진트리의 종류
1. 포화 이진 트리(Perfect binary tree)
- 모든 레벨의 노드가 가득 차있는 트리
- 노드가 2개의 자식을 가지고 있다.
- 차수(Degree)가 2.

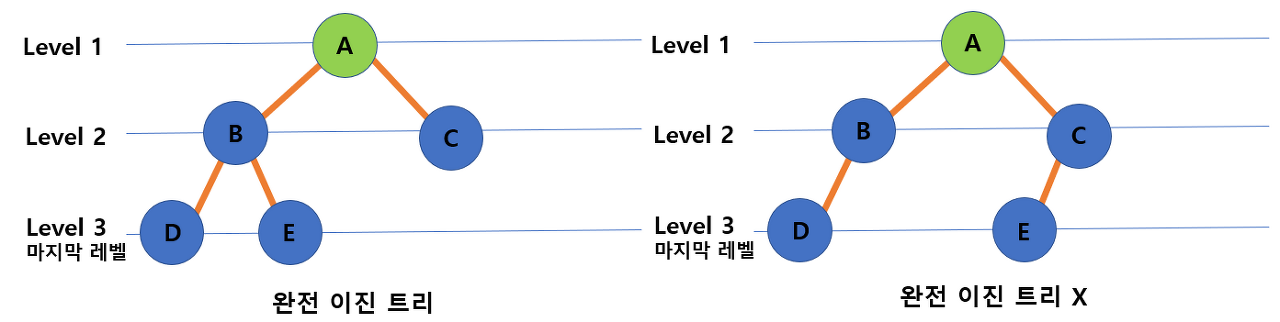
2. 완전 이진 트리(Complete binary search tree)
- 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있는 트리
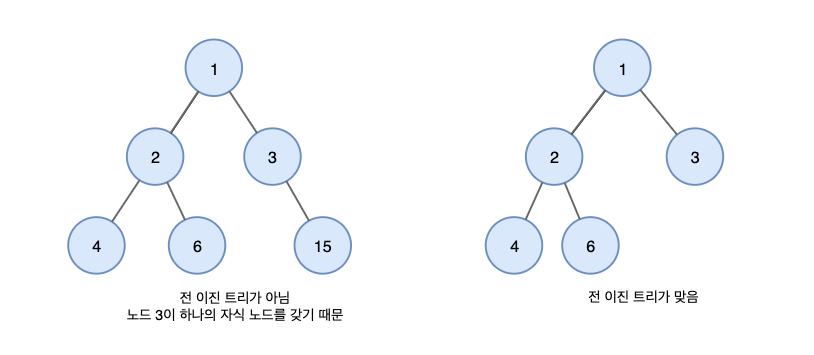
3. 정 이진트리(full binary tree)
- 모든 노드가 0개 또는 2개의 자식 노드를 갖는 트리
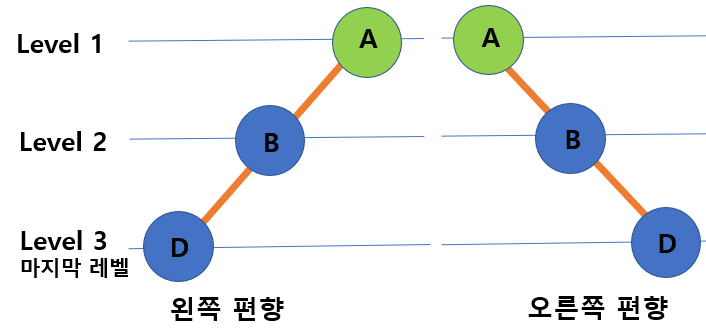
4. 편향 이진트리(skewed binary tree)
- 왼쪽 또는 오른쪽으로 편향되게 채워져있는 트리
- 각각의 높이에서 1개의 노드만 있다.
- 각 부모 노드가 오직 한 개의 연관 자식 노드를 갖는 트리
- 사향 이진 트리(Degenerate (or Pathological) Tree) 라고도 부른다.
- Linked List 성능과 동일하다.
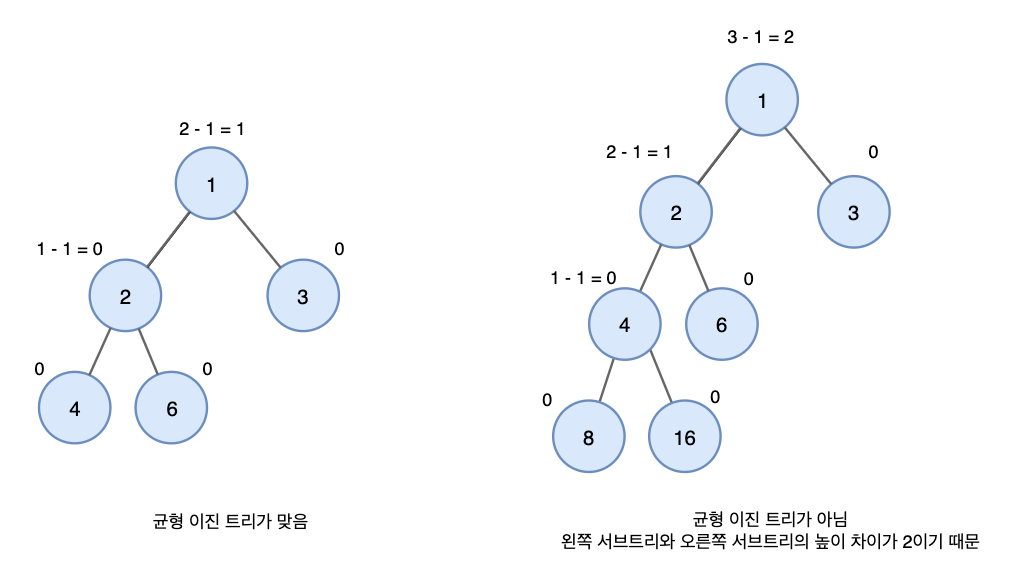
5. 균형 이진 트리(Balanced Binary Tree)
- 모든 노드의 왼쪽과 오른쪽 서브 트리의 높이가 1 이상 차이가 나지 않는 트리
6. 이진 탐색 트리(Binary Search Tree, BST)
이거 하려고 여기까지 왔다⎛⑉・⊝・⑉⎞
- 왼쪽 자식은 부모보다 작고 오른쪽 자식은 부모보다 큰 이진 트리
- 삽입, 삭제, 탐색과정에서 모두 트리의 높이만큼 탐색하기 때문에 O(logN)의 시간 복잡도를 가진다.
🐥 순회
- 전위순회 (preorder traversal)
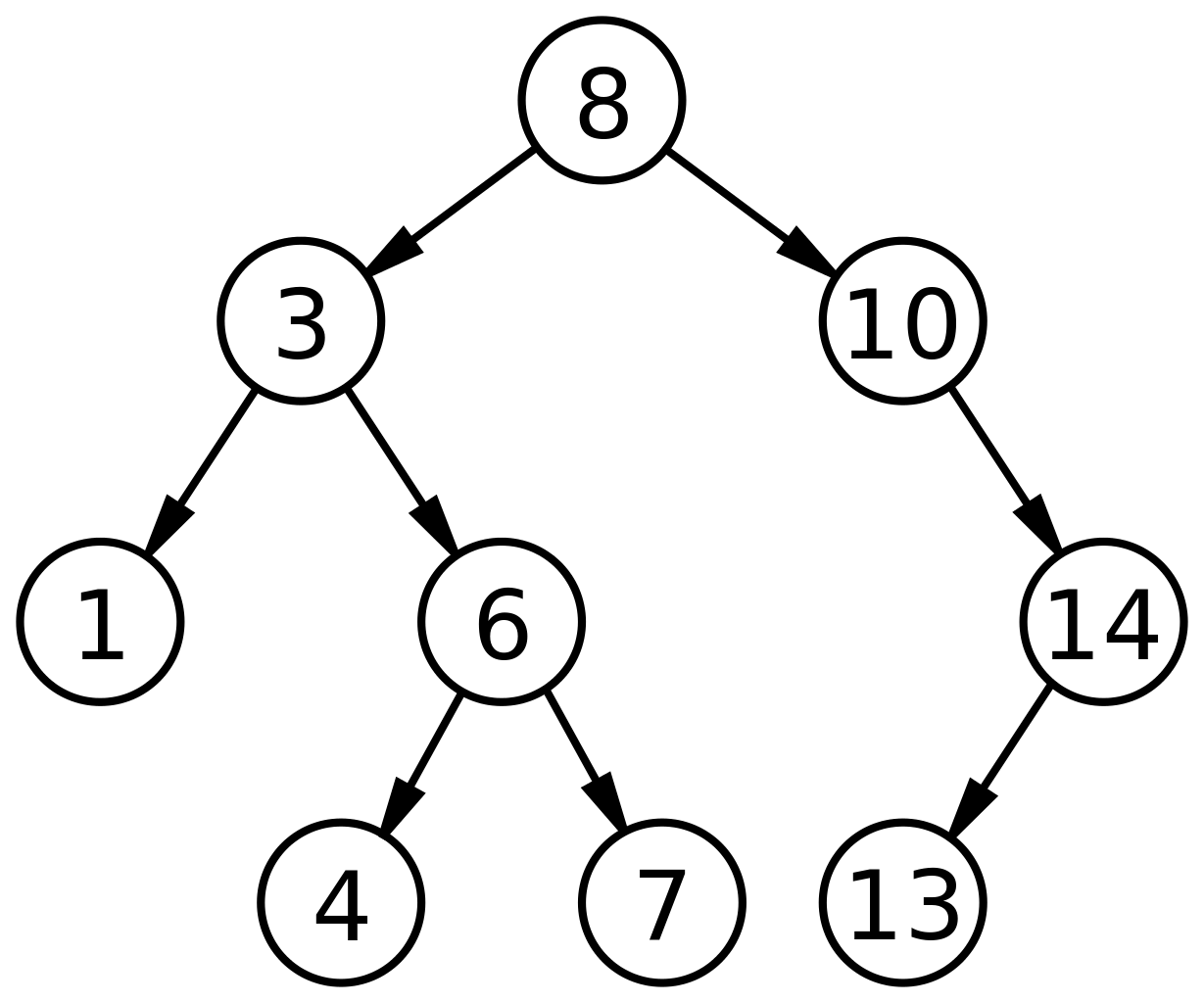
- 루트에서 시작해서 왼쪽 노드들을 순차적으로 탐색한 후, 오른쪽 노드 탐색!
루트 ➡️ 왼쪽 ➡️ 오른쪽
( 8 ➡️ 3 ➡️ 1 ➡️ 6 ➡️ 4 ➡️ 7 ➡️ 10 ➡️ 14 ➡️ 13)
public static void pre_order(Node node){
if(node == null) return;
System.out.print(node.value);
pre_order(node.left);
pre_order(node.right);
}- 중위순회 (inorder traversal)
- 왼쪽 자식 노드를 탐색 후, 루트 노드를 탐색하고, 오른쪽 자식 노드 탐색!
왼쪽 ➡️ 루트 ➡️ 오른쪽
( 1 ➡️ 3 ➡️ 4 ➡️ 6 ➡️ 7 ➡️ 8 ➡️ 10 ➡️ 13 ➡️ 14 )
public static void in_order(Node node) {
if(node == null) return;
in_order(node.left);
System.out.print(node.value);
in_order(node.right);
}- 후위순회(postorder traversal)
- 왼쪽 자식 노드 탐색 후, 오른쪽 자식 노드를 탐색하고, 루트 노드 탐색!
왼쪽 ➡️ 오른쪽 ➡️ 루트
(1 ➡️ 4 ➡️ 7 ➡️ 6 ➡️ 3 ➡️ 13 ➡️ 14 ➡️ 10 ➡️ 8 )
public static void post_order(Node node) {
if(node == null) return;
post_order(node.left);
post_order(node.right);
System.out.print(node.value);
}백준_1991_트리순회
https://www.acmicpc.net/problem/1991
풀이코드💡
import java.util.*;
import java.io.*;
public class BJ_1991_트리순회 {
static Node tree = new Node('A', null, null);
static int N;
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
N = Integer.parseInt(br.readLine());
for(int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine());
char root = st.nextToken().charAt(0);
char left = st.nextToken().charAt(0);
char right = st.nextToken().charAt(0);
insert(tree, root, left, right);
}
pre_order(tree);
System.out.println();
in_order(tree);
System.out.println();
post_order(tree);
System.out.println();
}
static class Node {
char value;
Node left;
Node right;
Node(char value, Node left, Node right) {
this.value = value;
this.left = left;
this.right = right;
}
}
public static void insert(Node temp, char root, char left, char right) {
if(temp.value == root) {
temp.left = (left == '.' ? null : new Node(left, null, null));
temp.right = (right == '.' ? null : new Node(right, null, null));
} else {
if(temp.left != null){
insert(temp.left,root,left,right);
}
if(temp.right != null) {
insert(temp.right, root, left, right);
}
}
}
public static void pre_order(Node node){
if(node == null) return;
System.out.print(node.value);
pre_order(node.left);
pre_order(node.right);
}
public static void in_order(Node node) {
if(node == null) return;
in_order(node.left);
System.out.print(node.value);
in_order(node.right);
}
public static void post_order(Node node) {
if(node == null) return;
post_order(node.left);
post_order(node.right);
System.out.print(node.value);
}
}
이제 안까먹었으면 좋겠는데... 할 수 있지..? \=͟͟͞͞(꒪ᗜ꒪ ‧̣̥̇)