Greedy Method

Greedy Method는 여러 알고리즘 패러다임 중 Brute Force(완전탐색)와 더불어 가장 직관적인 방법 중 하나이다. 재귀호출을 사용하여 해결 과정을 여러 조각으로 쪼갠 후, 각 단계를 해결하여 답을 완성해나가는 점에서 동적 계획법 알고리즘과 유사하다. 그러나 모든 선택지를 고려하여 최적의 답을 찾아내는 완전탐색과 동적 계획법 알고리즘과 달리 각 단계에서 찾을 수 있는 가장 최적의 방법을 선택한다. 즉, 탐욕법은 지금의 선택이 앞으로 남은 선택들에 어떠한 영향을 끼치는지 고려하지 않는다. 이러한 매커니즘은 항상 최적의 답을 만들어낼 수 있는가에 대한 의문점을 남긴다. 결론부터 말하자면 Greedy Method는 항상 최적해를 구할 수 없다. 따라서 다음과 같이 제한적으로 사용된다.

1. Greedy Method를 사용하여 항상 최적해를 구할 수 있는 문제의 경우, 동적 계획법보다 수행시간이 훨씬 빠르기 때문에 더 유용하다.(ex.일부 동전 교환 문제)
2. 시간이나 공간적 제약으로 인해 다른 방법으로 최적해를 찾기 어려운 경우 최적해가 아닌 근사해를 찾는 방법으로 타협할 수 있다. 즉, 적당히 좋은 답을 구하는 용도로 사용된다.

그리디 알고리즘의 가장 큰 오해는 쉽다는 것이다. 결론부터 말하자면 쉽지 않다. 그렇게 때문에 프로그래밍 대회에서 이 문제를 가장 나중에 푸는 것이 일반적이다. 이 알고리즘이 쉽지 않은 이유는 알고리즘의 결과가 근사해이기 때문에 알고리즘의 결과가 왜 최적이 되는지를 증명하는것이 어렵기 때문이다. 그리디 알고리즘의 결과가 최적임을 알리는 것을 정당성 증명이라고 한다. 앞서 서술하였듯 그리디 알고리즘의 결과는 항상 최적해를 보여주지 않기 때문에 만약 그리디 알고리즘으로 최적해라 판단되는 결과를 구했을 경우 정당성 증명을 통해 결과 값이 항상 옳음을 증명해야한다.

문제1. 동전 교환 문제(Coin Exchange)

문제 : 10원, 50원, 100원, 500원, 1000원이 있을 때, 2,750원를 교환할 수 있는 최소 동전 개수를 구하라.
이 문제는 그리디 알고리즘으로 해결할 수 있는 대표적인 문제이다. 가장 간단하게 생각해볼 수 있는 방법은 가장 큰 금액의 잔돈부터 차례로 계산하는 것이다. 그리고 이는 실제로 문제의 최적해이다.

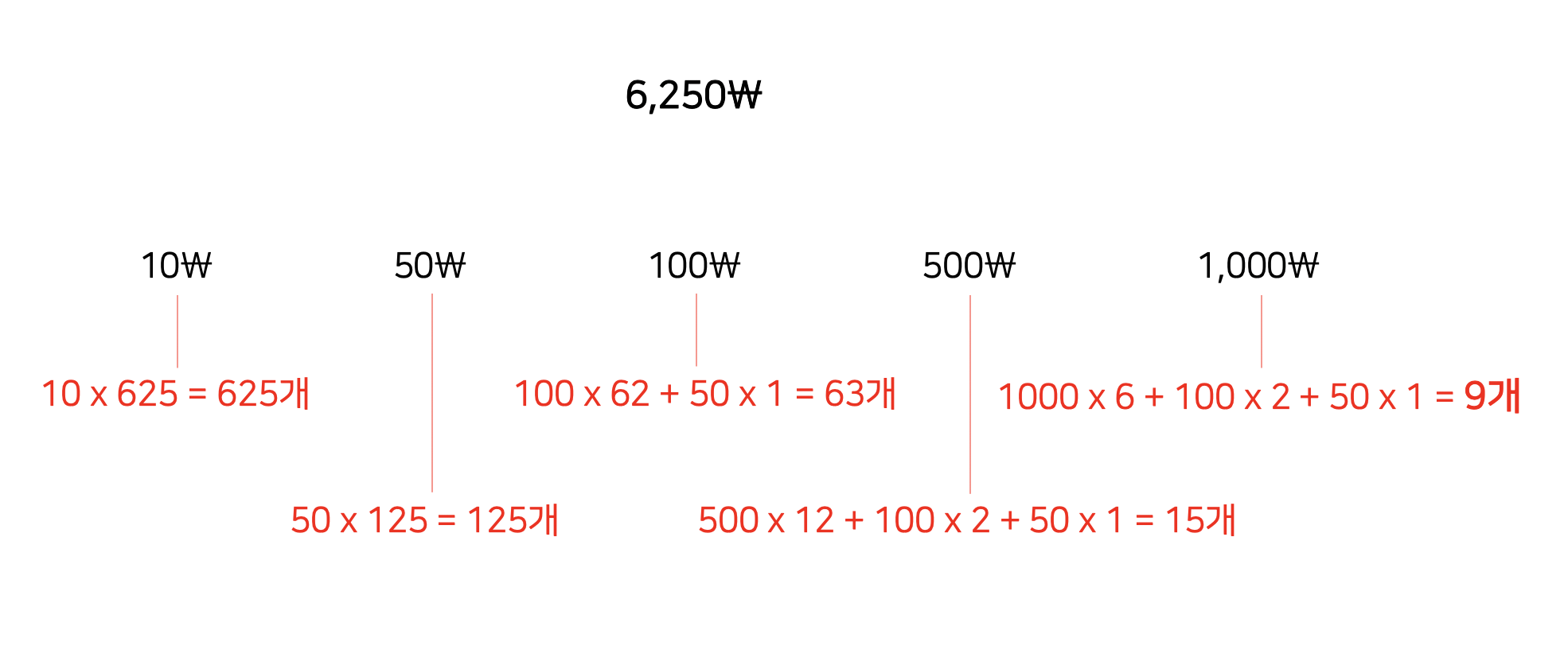
위 그림과 같이 가장 큰 금액의 잔돈인 1,000원부터 계산할 경우 9개의 동전을 사용하여 교환할 수 있다. 그리고 이 과정은 문제에 대한 정당성 증명이라고 할 수 있다.

int coins = [10, 50, 100, 500, 1000];

int main() {
	int money = 6250;	//교환할 돈
    	int changes = 0;	//동전 개수

	for(int i = coins.length - 1; i >= 0; i--) {
    		while(money >= coins[i]){
        		money -= coins[i];
        		changes++;
		}
    	}
}

문제2. 회의실 배정

문제 바로가기

문제 : 회사에 회의실이 하나밖에 없는데, n(<=100)의 팀이 각각 회의하고 싶은 시간을 다음 그림과 같이 제출했다고 한다. 두 팀이 동시에 회의실을 같이 쓸 수 없는 경우 최대로 많은 회의를 진행할 수 있는 최적해를 구하시오.

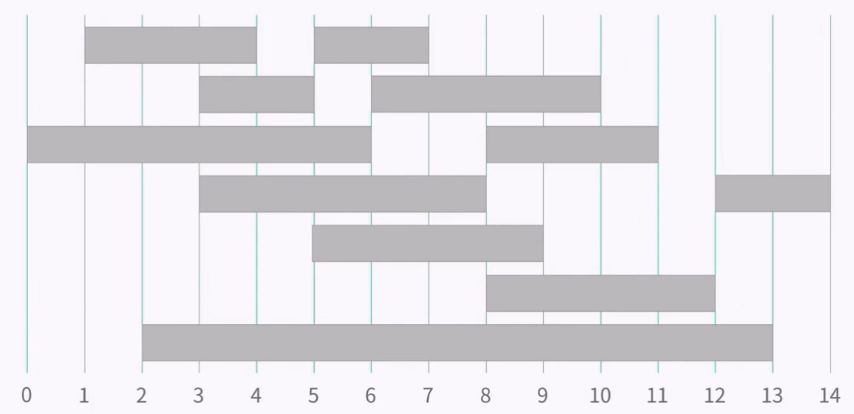
방법1. 회의시간이 짧은 회의를 먼저 배정한다?

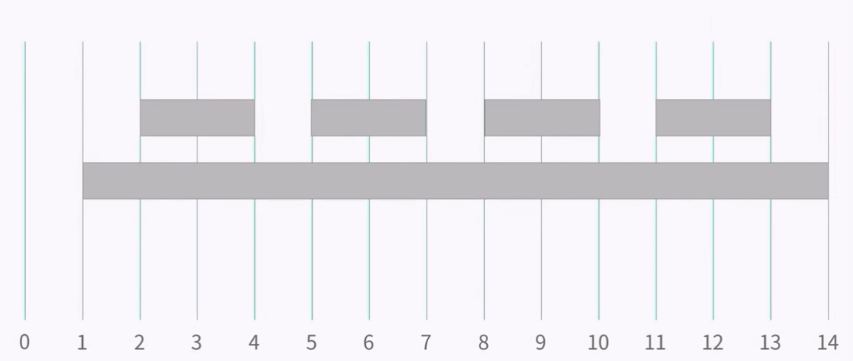
회의 시간이 짧은 회의를 먼저 배정하는 경우 위 그림과 같은 상황에서 최적해를 구할 수 없다. 따라서 다른 방법이 필요하다!

방법2. 일찍 시작하는 회의를 배정한다?

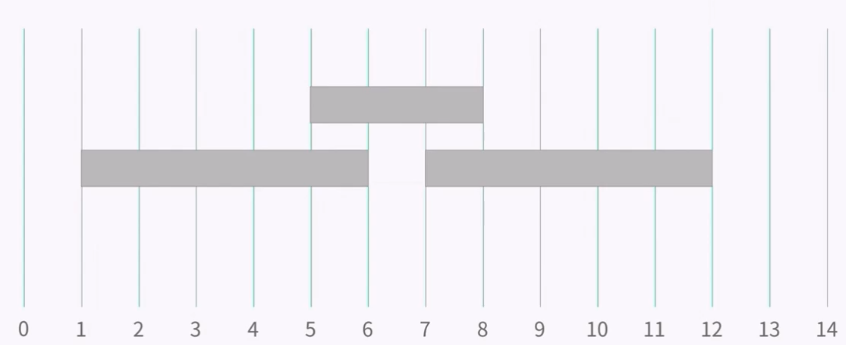
일찍 시작하는 회의를 배정할 경우 다음과 같은 상황에서 문제가 된다. 그럼 이러한 상황에 봉착했을 때를 대비하여 다른 Case를 고려하여 선택하면 되지 않나? 안타깝지만 그런 방법은 좋지 않다. 반례는 또다른 반례의 반례를 낳기 때문에 더 좋은 방법을 찾는 것이 중요하다.

방법3. 일찍 종료하는 회의를 배정한다?

struct Meeting{ 
  int begin, end;
}

bool compare(const Meeting &u, const Metting &v){
  //끝나는 시간이 같은 경우 시작시간을 기준으로 정렬한다.
  if(u.end == v.end){
    return u.begin < v.begin;
  } else{
    return u.end < v.end;
  }
}

int main() {
  int n;
  scanf("%d", &n);
  vector<Meeting> order(n);
  for(int i = 0; i < n; i++){
    scanf("%d %d", &order[i].begin, &order[i].end);
  }
  //order를 compare함수의 Logic을 이용하여 정렬한다.
  sort(order.begin(), order.end(), compare);
  
  int earliest = 0; //다음 회의가 시작할 수 있는 가장 빠른 시간
  int ans = 0; //선택한 회의의 수
  for(int i = 0; i < n; i++) {
    if(earliest <= order[i].begin) {
      earliest = order[i].end;
      ans++;
    }
  }
  printf("%d\n", ans);
  return 0;
}

문제3. 문자열 합치기

문제 바로가기

Hint : 우선순위 큐

주어진 문자열들의 길이를 오름차순으로 정렬하고 맨 앞의 가장 작은 두 값을 더한 값을 ret에 더해주고 그 값을 다시 정렬된 배열의 적합한 위치에 넣어준다.

int concat(const vector<int> lengths){
    priority_queue<int, vector<int>, greater<int> > pq;
    for(int i = 0; i < lengths.size(); i++)
        pq.push(lengths[i]);
    int answer = 0;
    while(pq.size() > 1) {
        int min1 = pq.top(); pq.pop();
        int min2 = pq.top(); pq.pop();
        pq.push(min1 + min2);
        answer += min1 + min2;
    }
    return answer;
}

정리

그리디 알고리즘은 문제를 해결하는 단계를 쪼개어 각 단계에서 선택할 수 있는 최적의 결과를 선택한다. 그렇기 때문에 이후의 선택을 고려하지 않아 항상 최적해를 보장하지 않는다. 제약에 의해 최적해를 구할 수 없거나 구하기 어려울 때 근사해를 구하기 위해 사용되거나 일부 문제에서 최적해를 구할 때 사용된다. 이때 결과가 최적해인지를 증명하는 과정이 필요하며 이를 정당성 증명이라고 한다. 그리디 알고리즘을 이용하여 최적해를 구했을 경우 동적 계획법 등의 다른 알고리즘에 비해 비교적 빠른 수행시간을 보여준다.