1. 그리디(탐욕) 알고리즘
-
동적 프로그래밍(dp) 사용 시 지나치게 많은 일을 한다는 것에서 착안하여 고안된 알고리즘이다. dp를 대체한다는 개념 보다는 같이 쓰이며 서로 보완하는 개념이다.
-
미래를 생각하지 않고 각 단계에서 가장 최선의 선택을 하는 기법이다.
예시)
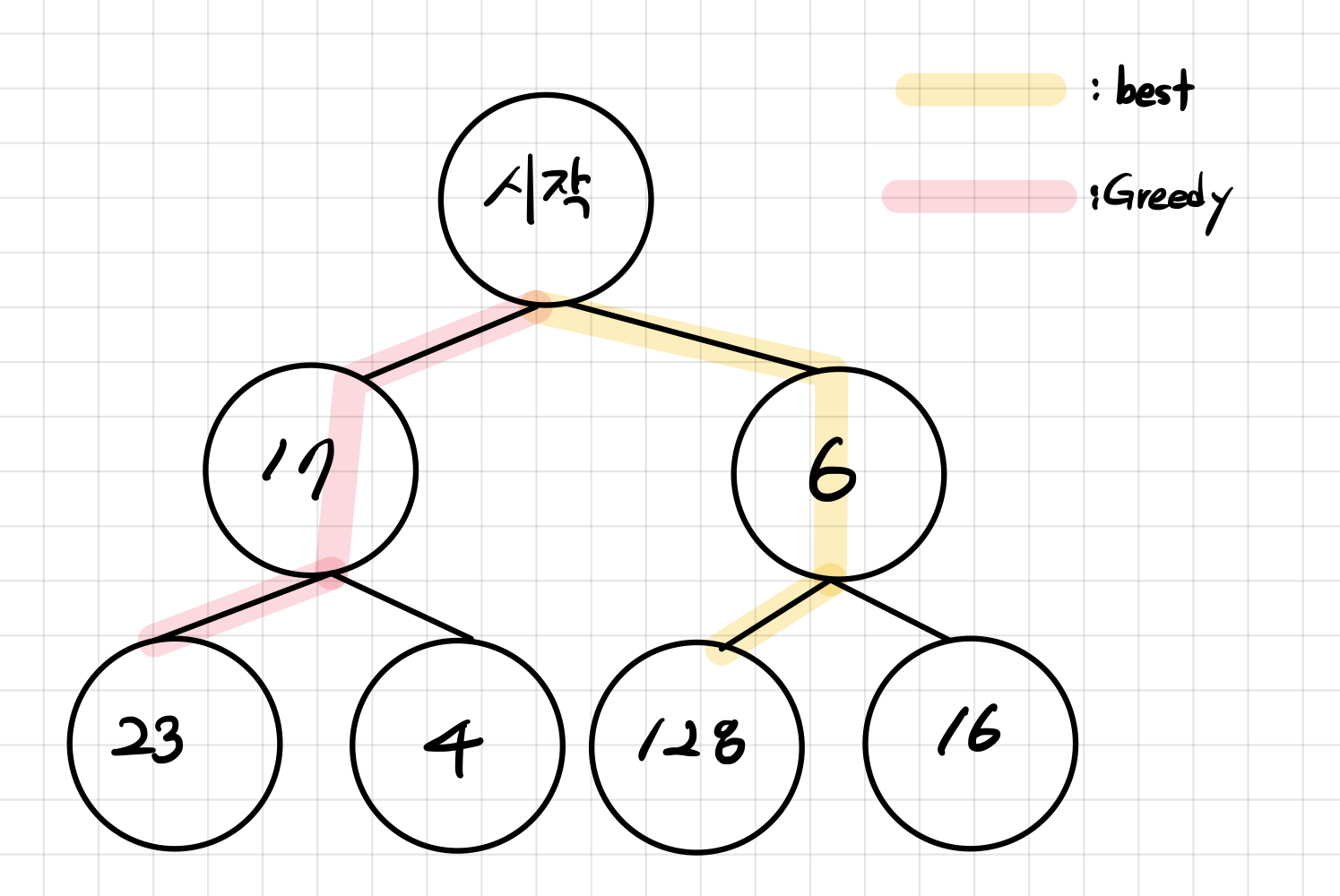시작 지점에서부터 시작하여 가장 큰 수를 구하는 문제가 있다고 가정해보자.
우리는 '시작 - 6 - 128'을 거치는 경로가 가장 큰 수를 도출할 수 있다는 것을 알 수 있다.
하지만 그리디 알고리즘은 '시작 - 17 - 23' 을 거치는 경로가 가장 좋은 것이라고 판단한다(현재 상황에서 가장 좋은 결과를 선택하기 때문이다. 17 vs 6 인 상황에서는 17이 가장 좋은 결과이고, 23 vs 4 인 상황에서는 23이 가장 좋은 결과이다)
그래서 사실, 위 문제에서는 그리디 알고리즘을 쓰면 안된다.
-
그리디 알고리즘을 사용하기 위해서는
- 그리디한 선택으로 인해 전체 문제의 최적해를 반드시 도출할 수 있어야 한다.
- 문제에 대한 최종 해결 방법이 부분 문제에 대해서도 또한 최적의 해결방법이다.
이 두 가지 조건을 만족해야 한다.
- 그리디 알고리즘이 통하는 문제들을 한 번 보자.
예시)
거스름돈 문제
당신은 음식점의 계산을 도와주는 점원입니다. 카운터에는 거스름돈으로 사용할 500원, 100원, 50원, 10원 동전이 무한개 존재합니다. 손님에게 거슬러 줘야 할 돈이 N원일 때 거슬러주어야 할 동전의 최소 개수를 구하라. 단, 거슬러 줘야 할 돈 N은 항상 10의 배수이다.
해답
def solution(money):
answer = 0
change = [500, 100, 50, 10]
remain = money
for i in change:
answer += remain // i
remain = remain % i
return answer- 조건에서는 '최소 개수'를 구하는 문제이므로 가장 큰 단위부터 거슬러주고 나머지를 그 다음 단위의 화폐로 거슬러 주는 것 이라는 해결 방법을 떠올릴 수 있다.(그리디 알고리즘)
- 거스름돈 문제는 가지고 있는 동전 중 '큰 단위'의 동전이 항상 '작은 단위'의 배수이므로(500원은 100원 5, 100원은 50원 2, 50원은 10원 * 5) 작은 단위 동전을 조합해 다른 해가 나올 수 없기 때문에 그리디 알고리즘을 사용할 수 있다.
2. 브루트 포스 알고리즘
-
brute: 무식한 / force:힘 -> '무식한 힘'
-
완전탐색 알고리즘으로써, 가능한 모든 경우의 수를 모두 탐색하면서 요구조건에 충족되는 결과만을 가져온다.
-
예외없이 100%의 확률로 정답만을 출력한다.
-
브루트 포스 알고리즘 설계의 가장 기본적인 접근 방법은 해가 존재할 것으로 예상되는 모든 영역을 전체 탐색하는 방법이다.
-
선형 구조를 전체적으로 탐색하는 순차 탐색, 비선형 구조를 전체적으로 탐색하는 깊이 우선 탐색(DFS, Depth First Search)과 너비 우선 탐색(BFS, breadth first search)이 가장 기본적인 도구이다.
-
깊이 우선 탐색(DFS)이 브루트 포스와 관련이 깊다.
-
너비 우선 탐색(BFS)
: 그래프에서 완전탐색 방법 중 하나. 탐색트리의 루트노드부터 목표노드를 만날 때까지 단계별로 횡방향으로 탐색을 진행해 나가는 방식.
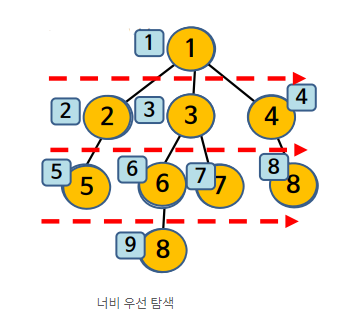: 장점으로는, 출발노드에서 목표노드까지의 최단 길이 경로를 보장한다.
: 단점으로는, 경로가 매우 길 경우에는 탐색 가지가 급격히 증가하므로 많은 기억 공간을 필요로 한다.
: 해가 존재하지 않는다면 유한 그래프의 경우에는 모든 그래프를 탐색한 후에 실패로 끝난다. 무한 그래프의 경우에는 결코 해를 찾지도 못하고, 끝내지도 못한다. -
브루트 포스 알고리즘 예제
- 거스름돈을 지불할 수 있는 방법의 수와 최소 동전의 개수 구하기
: 10원과 50원으로 120원을 지불할 수 있는 모든 방법의 수와 최소 동전의 개수를 구해보자. -> 주어진 동전의 종류가 2가지이므로 2차원 즉 행렬의 형태로 구조화하여 일반적 방법으로 해결할 수 있다. 행을 50원, 열을 10원으로 생각하고 구조화해보자.
위 행렬에서 행렬(0, 0)은 50원 동전 0개, 10원 동전은 0개를 지불하는 방법으로 생각할 수 있다. 따라서 행렬(1, 7)은 50원 동전 1개, 10원 동전 7개로 120원을 지불하는 방법이 된다.
구조화하고 행렬을 2차원으로 탐색하여 120을 이루는 모든 경우의 수를 조사하여, 구한 값들 중 행의 값 + 열의 값의 합의 최소값을 찾으면 최소 동전의 수가 된다.
위 행렬을 탐색해 보면 120원을 지불할 수 있는 경우의 수는 (0, 12), (1, 7), (2, 2)의 3가지이며, 이들의 사용한 동전의 수는 각 행과 열의 합이다.
따라서 사용한 최소 동전의 수는 이 값들 중 최소값이므로 4이다.
120원을 지불할 수 있는 모든 경우의 수 : 3가지, 최소 지불 동전의 수 : 4개
- 거스름돈을 지불할 수 있는 방법의 수와 최소 동전의 개수 구하기
출처
https://www.zerocho.com/category/Algorithm/post/584ba5c9580277001862f188
https://hcr3066.tistory.com/26
https://velog.io/@uoayop/%EB%83%85%EC%83%89-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://velog.io/@contea95/%ED%83%90%EC%9A%95%EB%B2%95%EA%B7%B8%EB%A6%AC%EB%94%94-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
