실습파일은 깃허브에 올려두었다
: https://github.com/CNU-Jiho-Jeong/jjh98/tree/main/%ED%94%84%EB%A1%9C%EA%B7%B8%EB%9E%98%EB%A8%B8%EC%8A%A4%20%EA%B3%BC%EC%A0%9C
1. 최적화 기법
1. 모멘텀

-
매개변수 α를 v에 곱해서 αv 항은 물체가 아무 힘도 받지 않을 때도 서서히 하강시키는 역할을 하게 된다. 물리에서의 마찰력이라고 생각하면 편하다.
-
모멘텀 파이썬 코드
import numpy as np
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr #η
self.momentum = momentum #α
self.v = None
def update(self, params, grads):
# update()가 처음 호출될 때 v에 매개변수와 같은 구조의 데이터를 딕셔너리 변수로 저장
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
params[key] += self.v[key]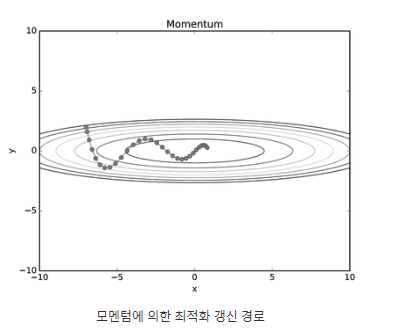
=> SGD와 비교했을 때 더 효율적인 경로로 최적해를 찾는 것을 확인할 수 있다.
2. AdaGrad
- 각각의 매개변수에 적응적으로 Adaptive 학습률 Learning rate을 조정하며 학습을 진행
- 학습률 값이 매우 중요(학습률 값이 너무 작으면 학습시간이 너무 길어지고, 학습률 값이 너무 크면 발산하여 학습이 제대로 이뤄지지 않는다.)
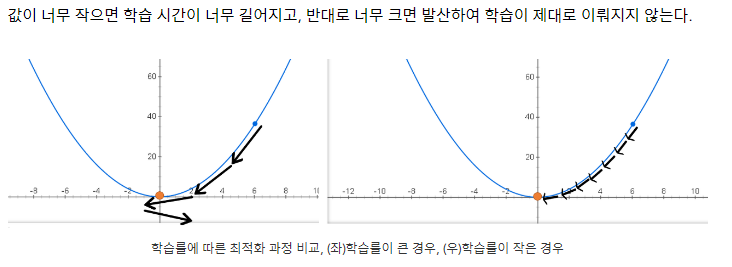
- 왼쪽 그래프는 학습률이 커서 3번만에 최솟점 근처에 도달하지만, 너무 크게 변해 최솟점을 지나친다. 다시 최솟점으로 가기 위해 방향이 바뀌지만 변화율이 커 최솟점에 도달하지 못하고 근처에만 도달 가능하다
- 오른쪽 그래프는 학습률이 작아 7번만에 최솟점에 도달하지만, 시간이 왼쪽보다 2배정도 더 걸린다.

- AdaGrad 파이썬 코드
class AdaGrad:
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
# 0으로 나누는 일이 없도록 1e-7을 더해줍니다. 이 값은 임의로 지정 가능합니다.3. Adam
- 모멘텀 + AdaGrad
- Adam 파이썬 코드
class Adam:
"""Adam (http://arxiv.org/abs/1412.6980v8)"""
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
#self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key]
#self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2)
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
#unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias
#unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias
#params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)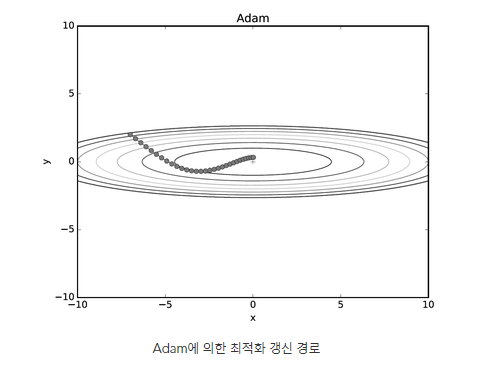
=> 학습의 갱신 강도를 적응적으로 조정해서 얻었기 때문에 모멘텀 방법과 비교해서 좌우 흔들림이 적음
4. SGD(확률적 경사 하강법), 모멘텀, AdaGrad, Adam 최적화 기법 비교
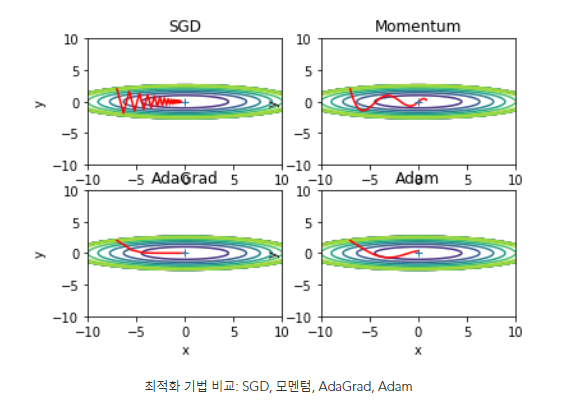
=> 풀어야할 문제에 따라, 하이퍼파라미터를 어떻게 설정하느냐에 따라 결과가 바뀌므로, 넷 중 무엇이 가장 뛰어나다 말할 수는 없다
5. MNIST 데이터셋으로 본 갱신 방법 비교 (과제에서도 MNIST 데이터셋을 활용하였다.)
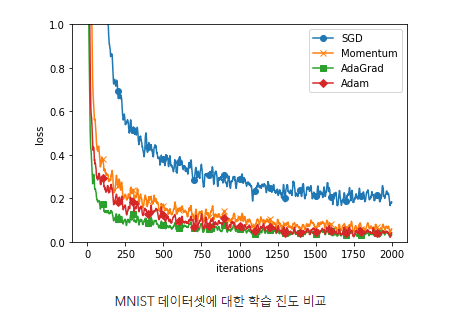
=> SGD의 학습 진도가 가장 느리고 나머지 세 기법의 진도는 비슷하지만 AdaGrad가 조금 더 빠르다는 걸 알 수 있다. (일반적으로 SGD 보다 다른 세 기법이 빠르게 학습하고, 때로는 최종 정확도도 높게 나타난다. 이번 과제에서도 그랬다. SGD 대신 Adam을 쓰니 최종 정확도가 91%에서 97%까지 올랐다.)
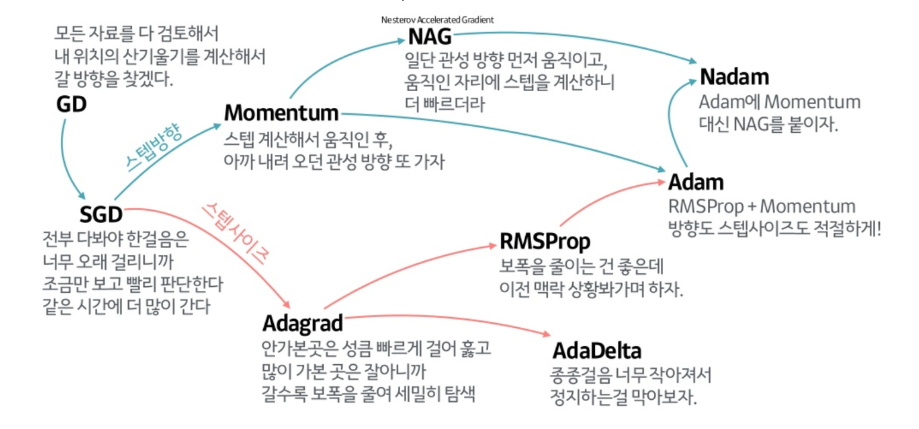
(++ 최적화기법들을 아래 그림을 보고 참고하자)
2. CPU vs GPU
1. CPU
- CPU는 컴퓨터의 두뇌를 담당
- 데이터 처리와 더불어 프로그램에서 분석한 알고리즘에 따라 다음 행동을 결정하고 멀티태스킹을 위해 나눈 작업들에 우선순위를 지정하고 전환하며 가상 메모리를 관리하는 등 컴퓨터를 지휘하는 역할을 수행
- 순차적인 작업 (Sequential task) 에 더 강점이 있다.
2. GPU
- 비디오, 즉 픽셀로 이루어진 영상을 처리하는 용도로 탄생
- CPU에 비해 반복적이고 비슷한, 대량의 연산을 수행하며 이를 병렬적으로(Parallel) 나누어 작업하기 때문에 CPU에 비해 속도가 대단히 빠르다(과제에서도 GPU로 연산시 속도가 더 빨랐다).
- 병렬적인 작업 (Paralell task) 에 더 강점이 있다.
3. pytorch
1. dropout
- 신경망에서 유닛을 제거하여 다수의 아키텍처를 동시에 시뮬레이션하는 머신 러닝 기술. 과적합이 될 가능성을 획기적으로 줄일 수 있음.
- 신경망 실습 과제에서도 신경망의 일반화 성능을 높이기 위해(과적합을 방지하기 위해) 쓰였다.
- torch.nn.Dropout(p=0.5, inplace=False)
- p: drop_prob, 노드를 얼만큼 활용 안 할지 (요소가 0이 될 확률, Default: 0.5)
- inplace: true로 설정하면 제자리에서 작업 수행 (Default: False)
- 신경망 실습 과제에서 p=0.5로 쓰임
2. Linear
- 파이토치에서 선형회귀 모델은 nn.Linear() 함수에 구현되어 있다.
- nn.Linear(input_dim,output_dim)
-입력되는 x의 차원과 출력되는 y의 차원을 입력해주면 된다.
3. tensor GPU 연산
-
pytorch tensor를 GPU에 올리기
- device: 해당 tensor가 CPU, GPU 중 어디에 있는지 확인할 때 사용한다.ex1> CPU에 있는 경우
print(a.device)
-> cpuex2> GPU에 있는 경우
print(a.device)
-> cuda:0- cuda.is_available(): GPU(cuda)를 사용할 수 있는지 확인할 때 사용한다.
- to('cuda'): tensor를 GPU에 올릴 때 사용한다.
- to('cpu'): tensor를 다시 CPU에서 계산할 때 사용한다.
ex>
a = torch.tensor([1, 2, 3, 4])
print(a.device)
->cpua = a.to('cuda') # a 라는 tensor를 GPU에 올린다
print(a.device) # a가 GPU에 올라갔으므로 해당 tensor가 어디에 있는지 확인하면
-> cuda:0 # GPU에 있다.a = a.to('cpu') # a라는 tensor를 CPU에 올린다.
print(a.device) # a가 CPU에 올라갔으므로 해당 tensor가 어디에 있는지 확인하면
-> cpu # CPU에 있다.- requires_grad: True로 설정 시 모든 연산들을 기억
- retain_grad(): 해당 변수에 대한 gradient 연산을 기억 -> 이것을 하지 않으면 중간 변수에 대한 gradient는 저장 안됨
- backward(): 기억한 연산들에 대해서 gradient 계산 -> grad attribute(속성)에 gradient 정보 축적
- detach(): 계산 정보를 더 이상 기억하지 않음(stop tracking history)
- torch.no_grad(): torch.no_grad()를 사용하면 연산을 하는 동안 그 history를 기억하지 않는다. 그러므로 memory를 덜 사용한다. 때문에 gradient 계산이 필요없는 경우 즉, training이 아닌 inference를 하는 경우 사용한다. 더 적은 memory를 사용하기 때문에 더 빠른 계산이 가능해진다.
4. numpy 함수
1. np.mean()
- 주어진 배열의 산술 평균 계산
- np.mean(배열) : 입력 배열을 평면화된 배열로 취급하고 이 배열의 산술 평균 계산
- np.mean(배열, axis=0) : 열을 따라 산술 평균 계산
- np.mean(배열, axis=1) : 행을 따라 산술 평균 계산
2. np.squeeze()
- 파이썬 넘파이 배열에서 크기가 1인 axis를 제거한다.
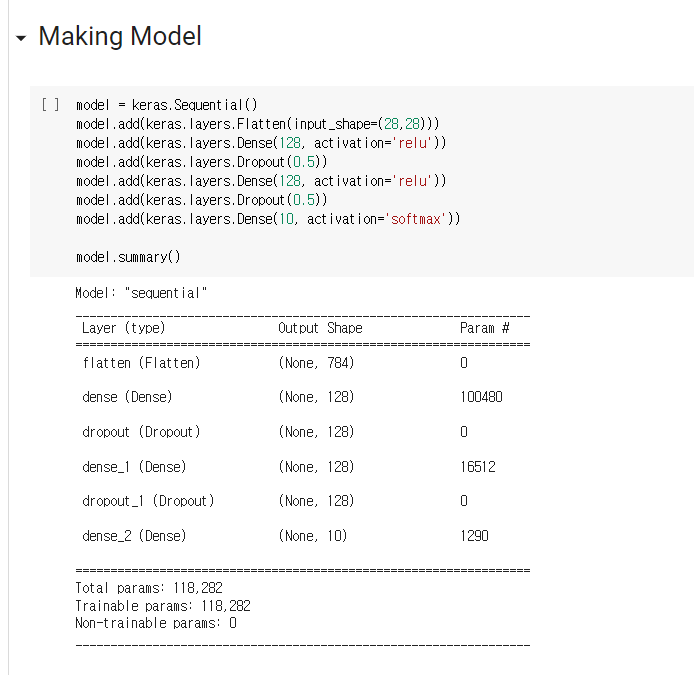
5. 신경망 실습 과제
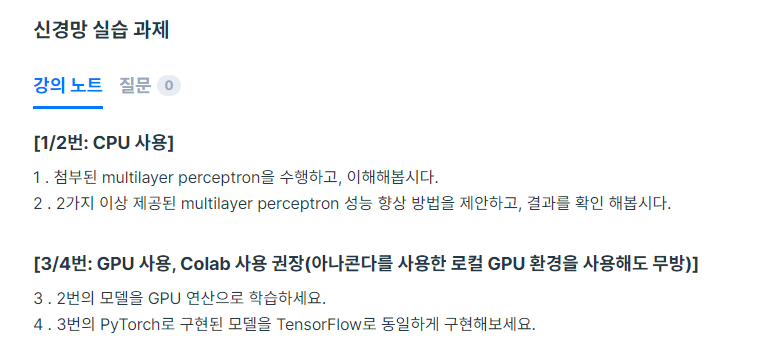
1. 과제 1
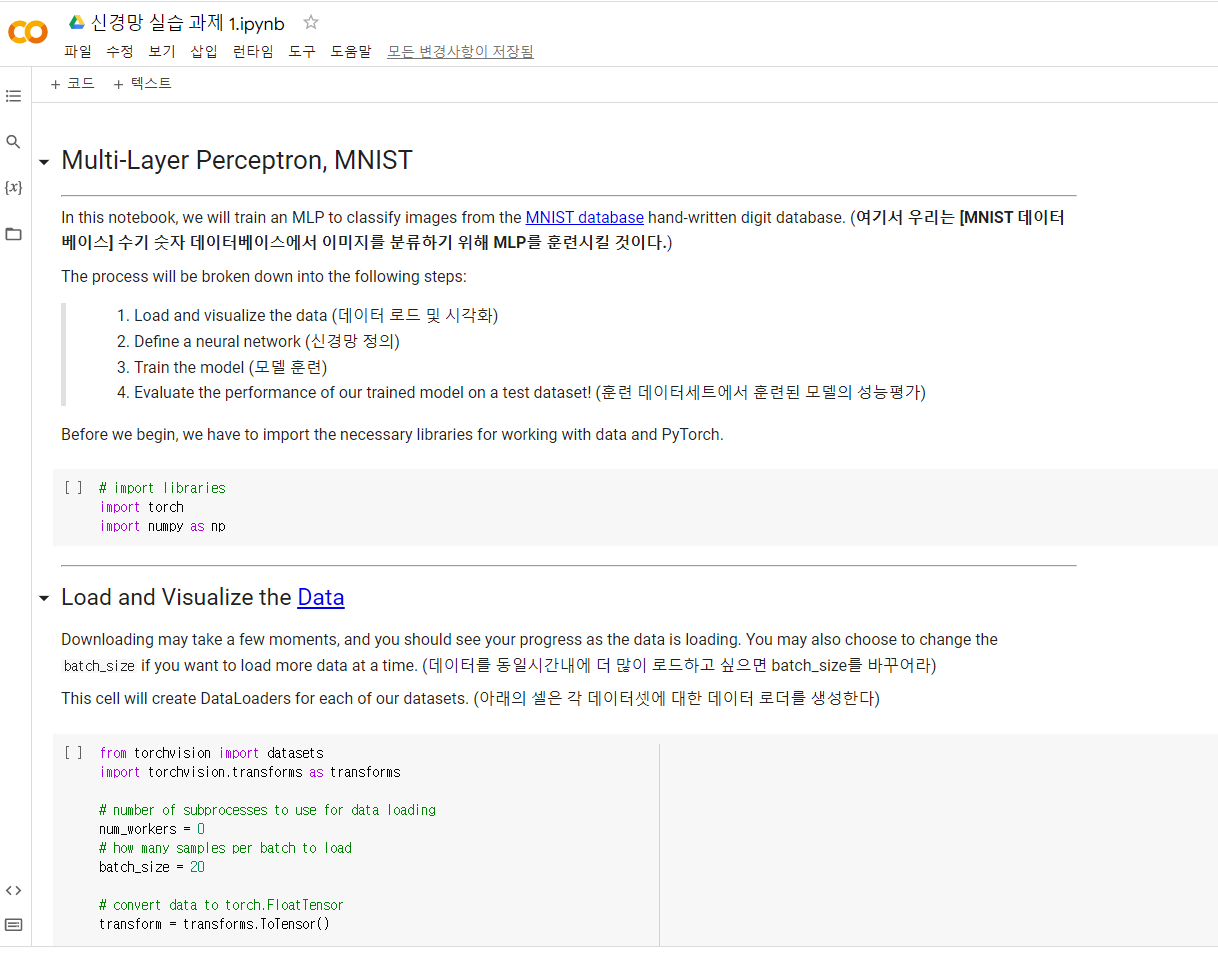
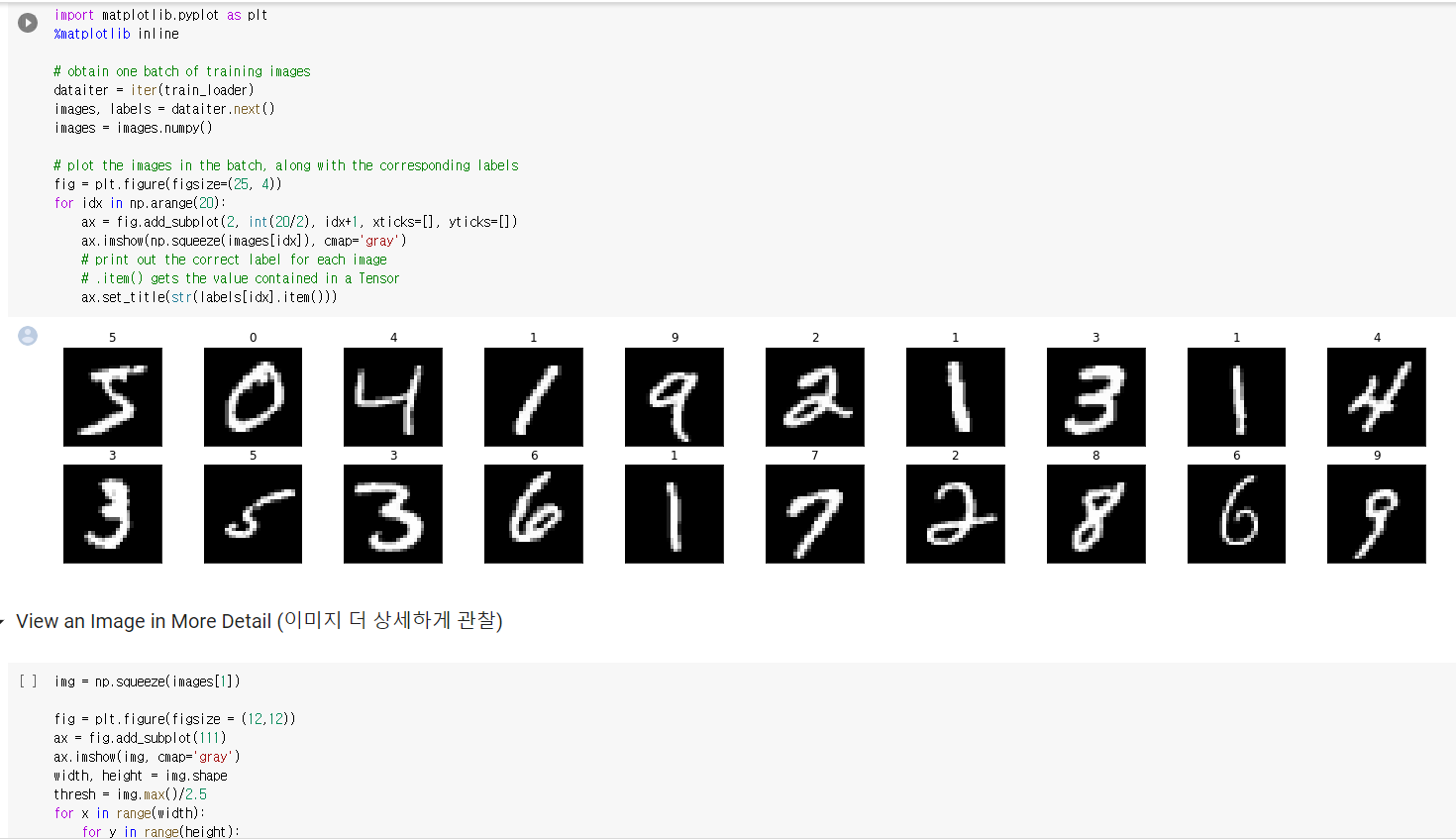

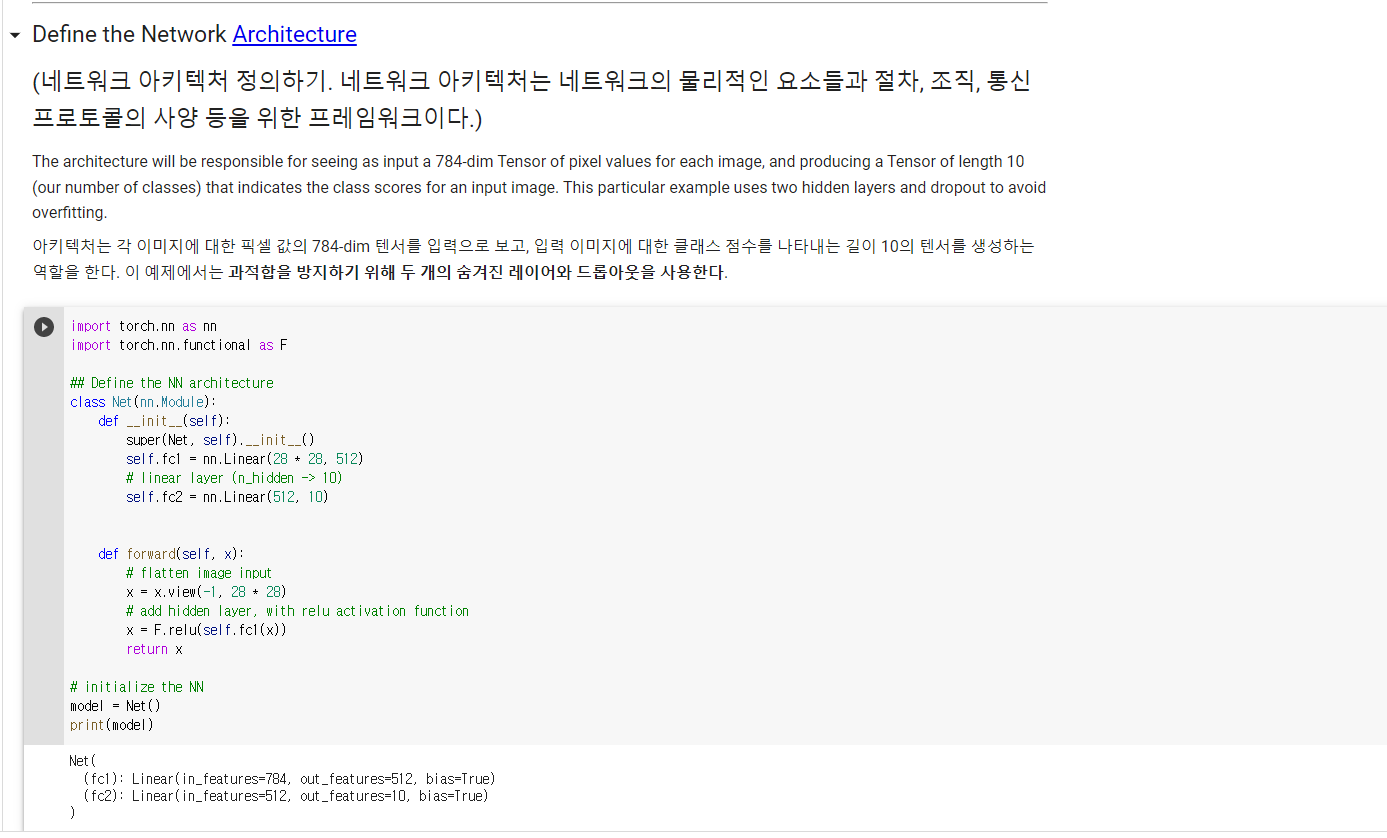
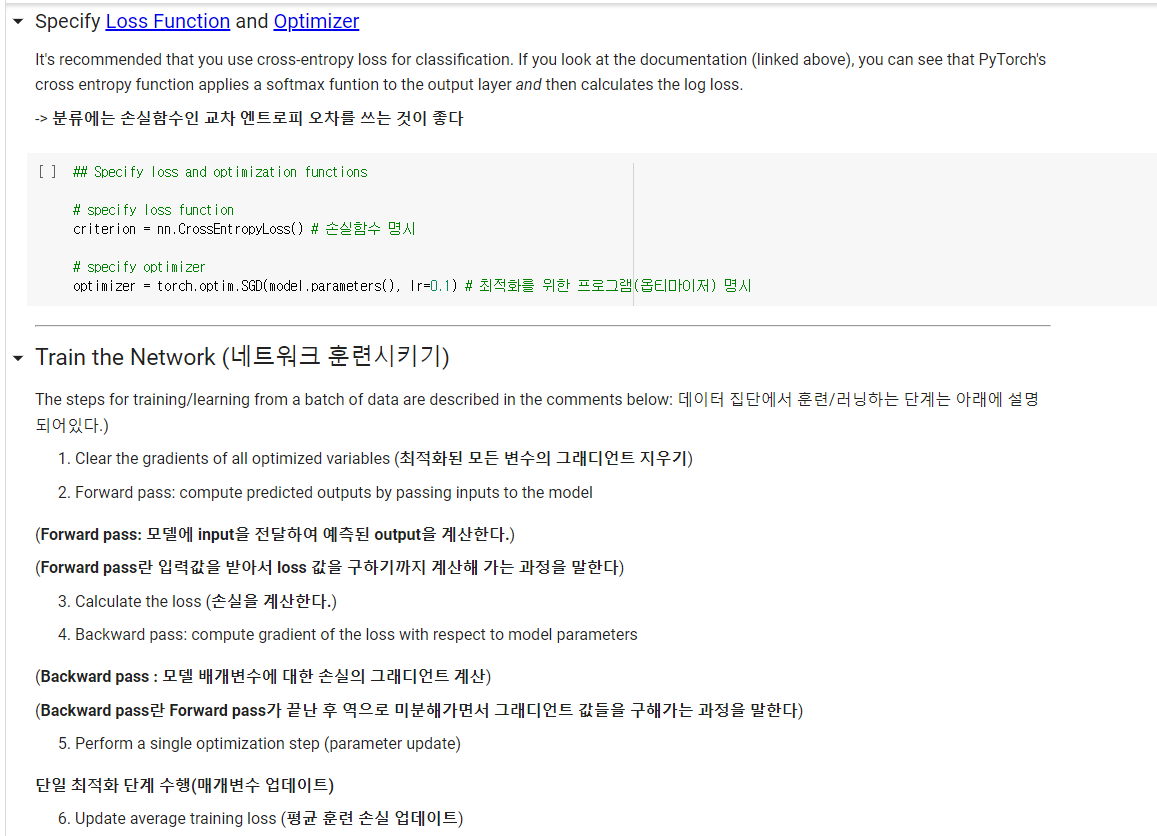




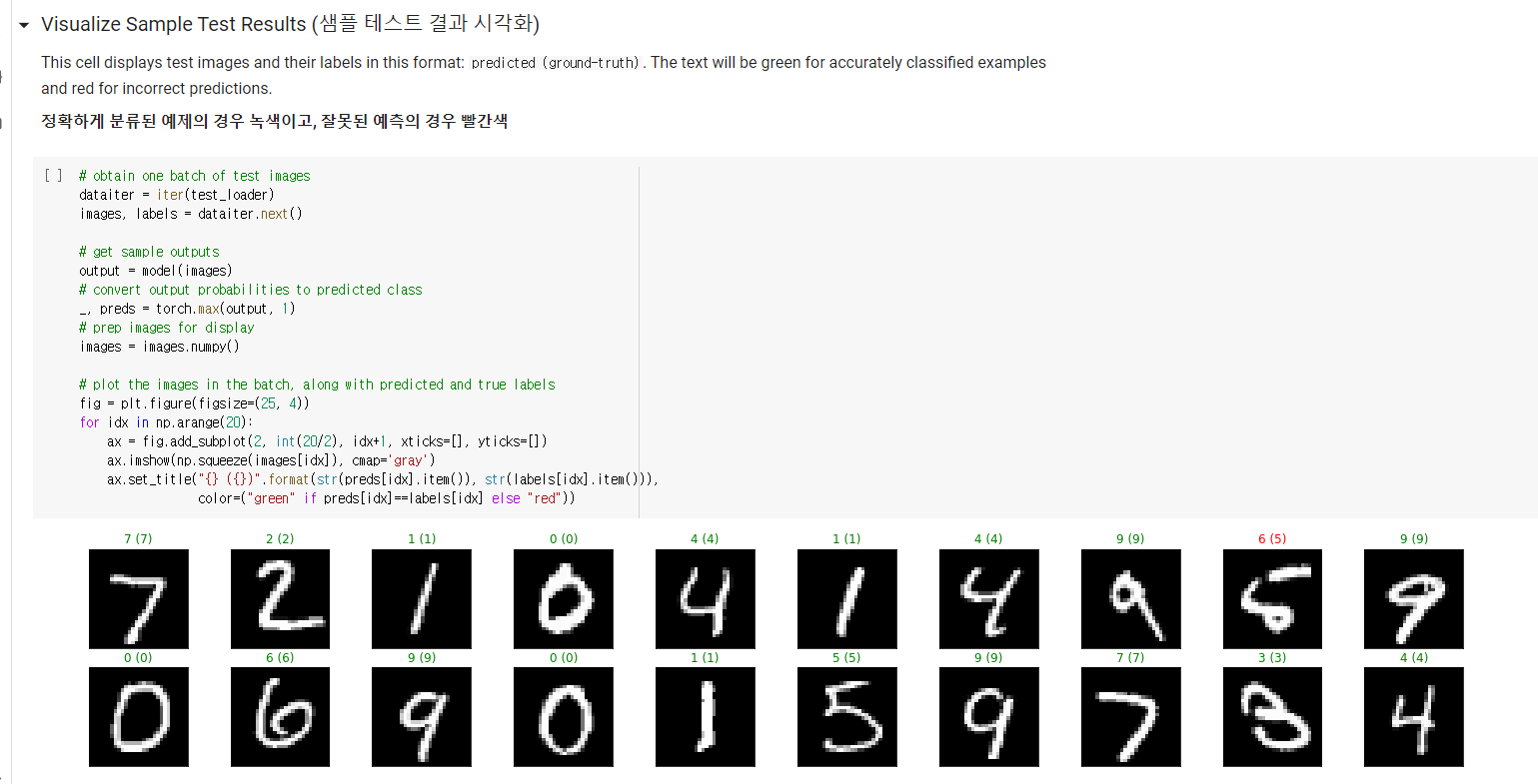
2. 과제 2,3,4
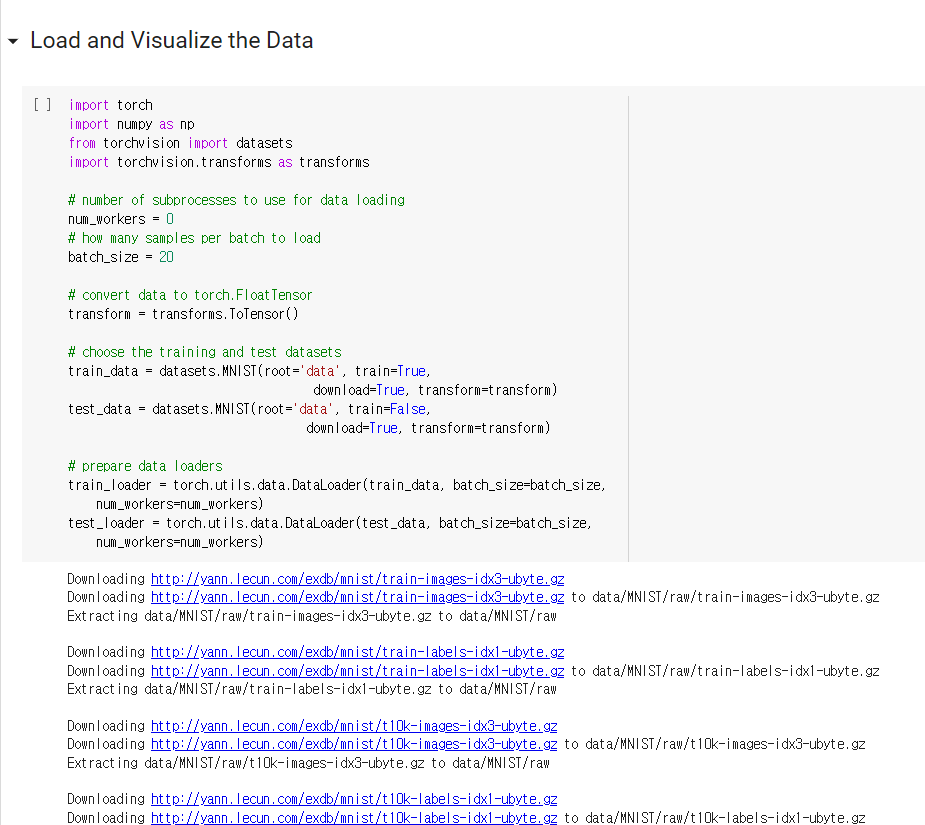
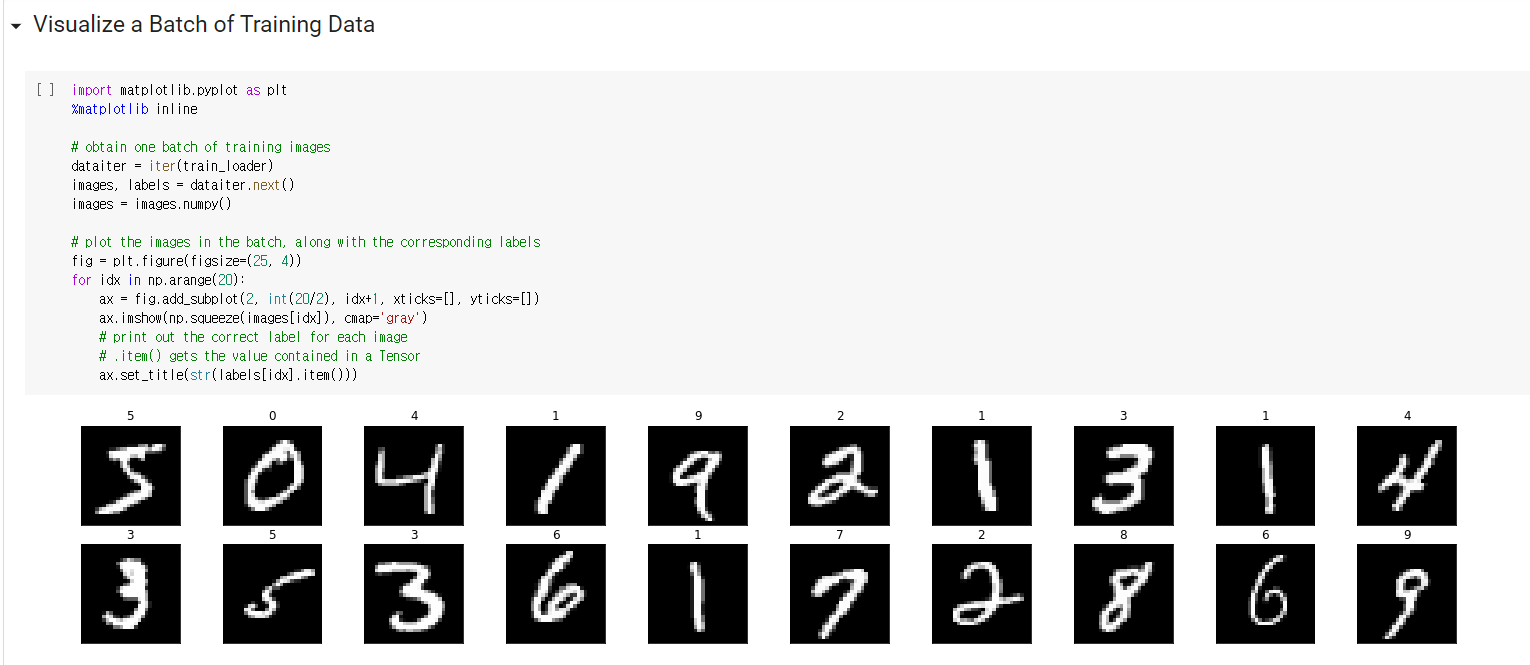
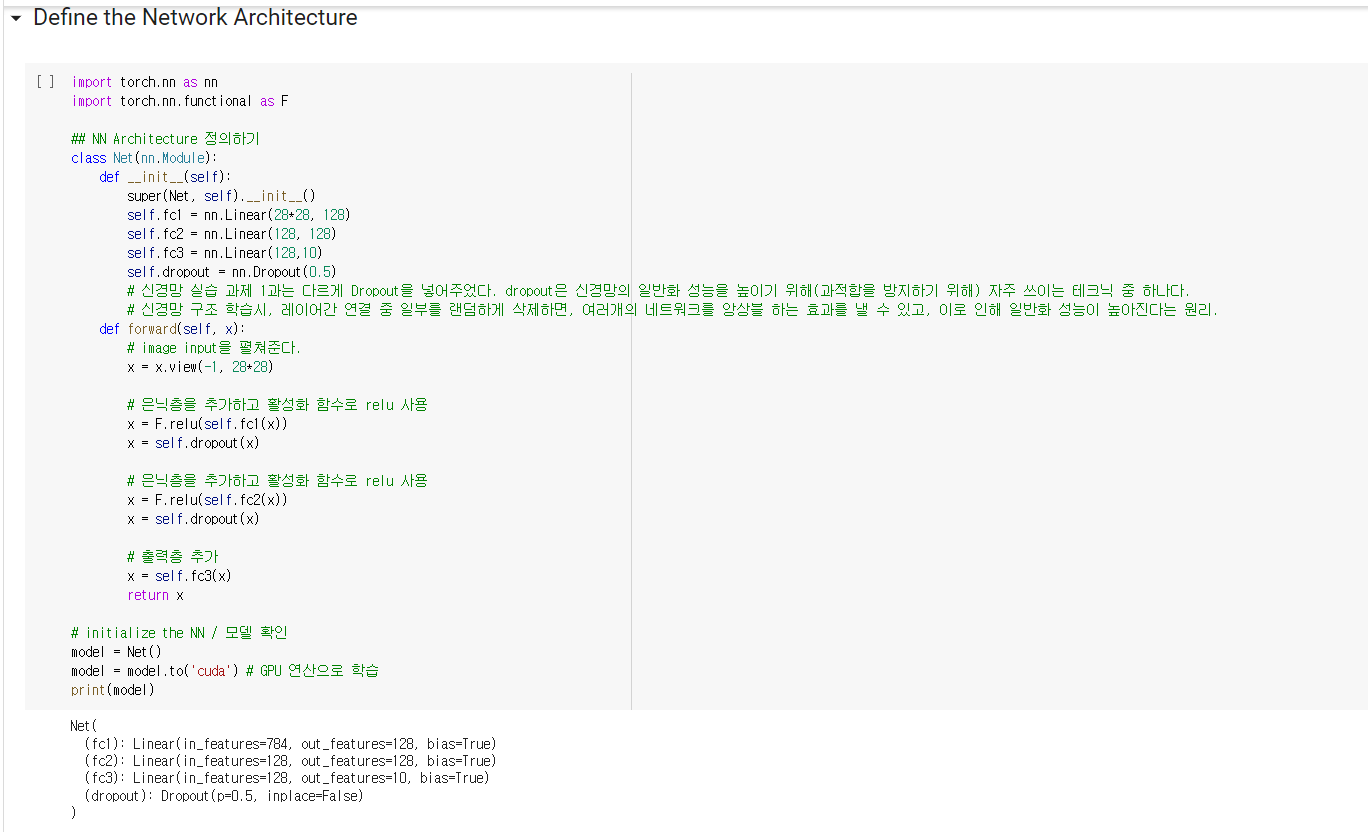

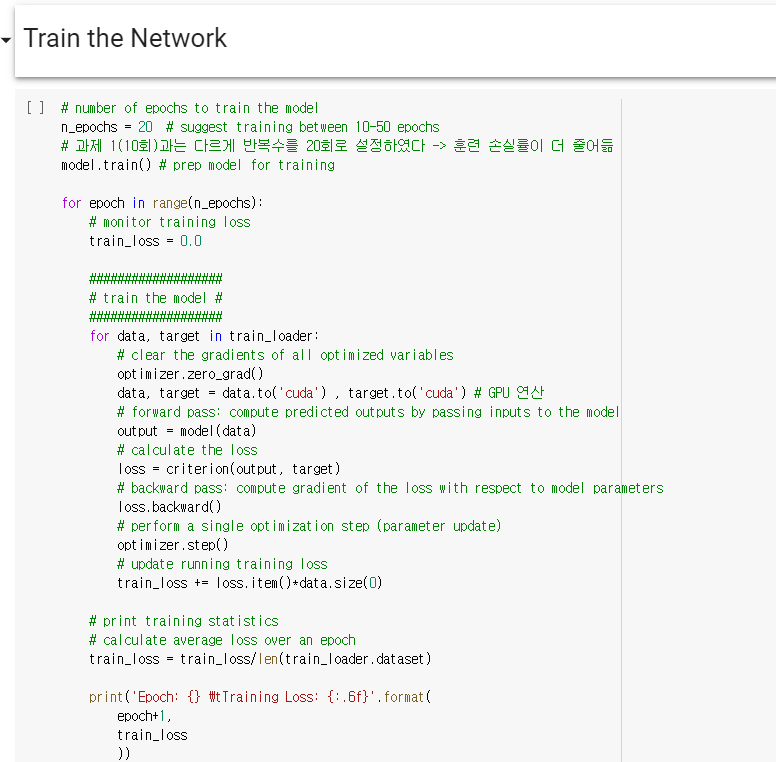
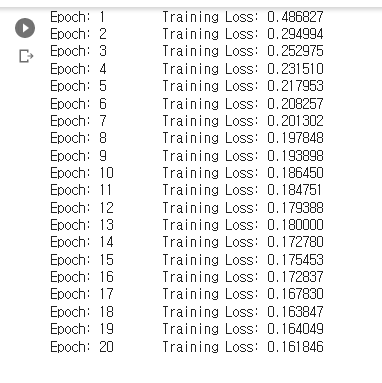
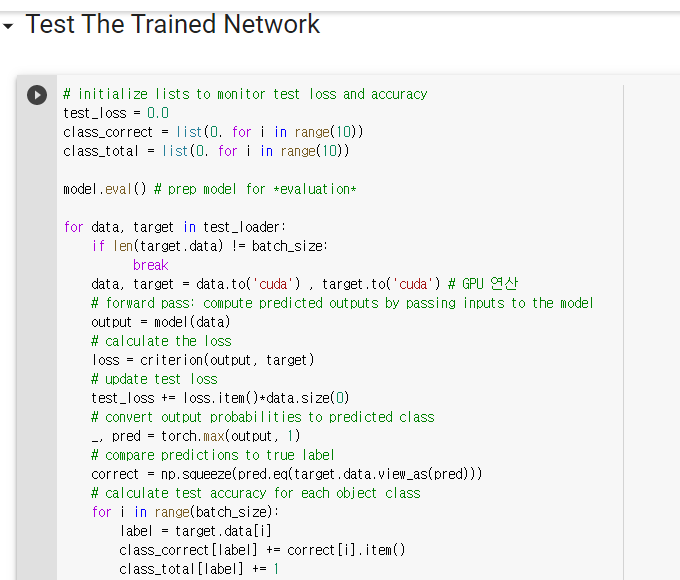





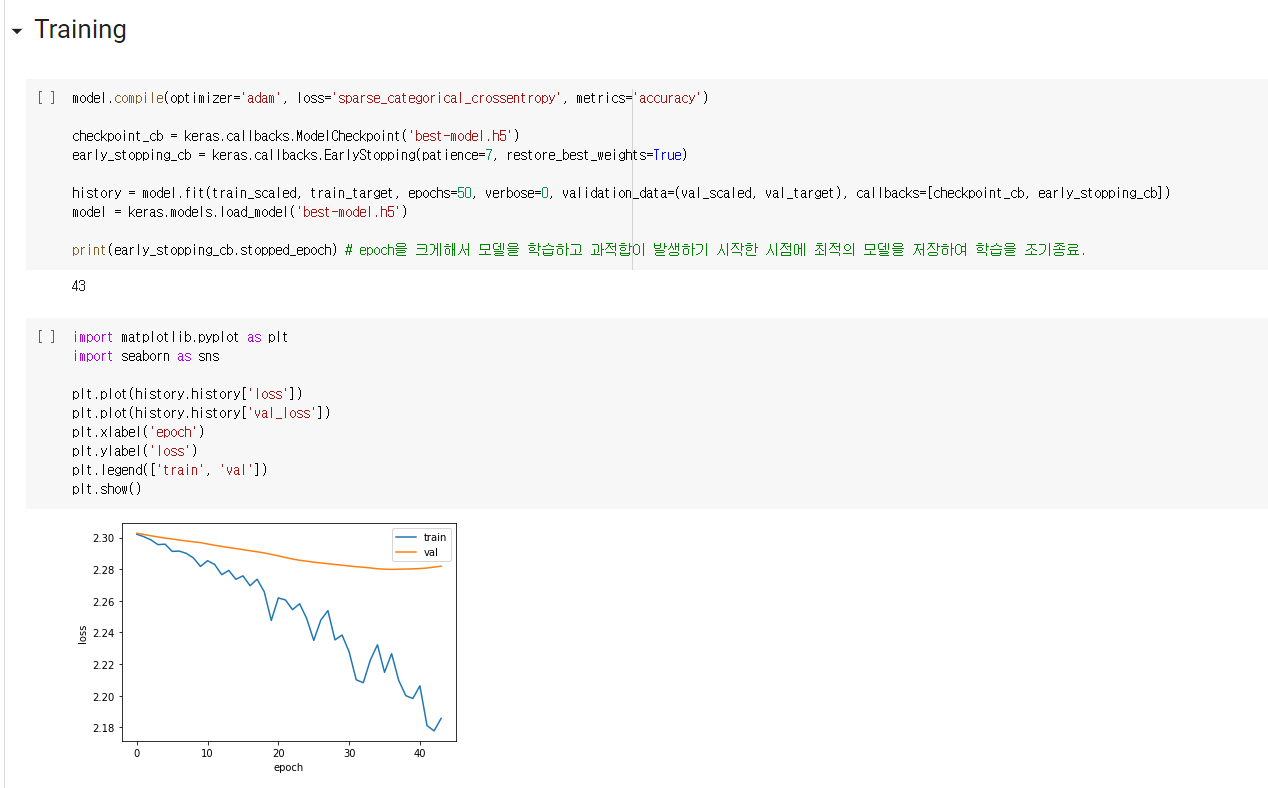

참고 사이트들
https://huangdi.tistory.com/7
https://m.blog.naver.com/gladiator67/222068617022
https://easy-going-programming.tistory.com/8
https://velog.io/@clayryu328/Weekly%EC%8B%A4%EC%8A%B55-multilayer-perceptron-with-mnist
https://qlsenddl-lab.tistory.com/28
https://m.blog.naver.com/fbfbf1/222480437930
https://m.blog.naver.com/gladiator67/222068617022
https://sdc-james.gitbook.io/onebook/2.-1/1./1.1.1.-cpu-gpu
https://championprogram.tistory.com/273
https://wandb.ai/wandb_fc/korean/reports/---VmlldzoxNDI4NzEy
https://jimmy-ai.tistory.com/101
https://www.delftstack.com/ko/api/numpy/python-numpy-mean/
