알고리즘 격파 모임 1주차

정지호·2022년 8월 8일

개인 실습 진행

목록 보기

12/41

내가 푼 문제들

1. 백준 10974 모든 순열

2. 백준 11653 소인수분해

3. 백준 1929 소수 구하기

4. 백준 2748 피보나치 수 2

5. 백준 8393 합

1. 백준 10974 모든 순열

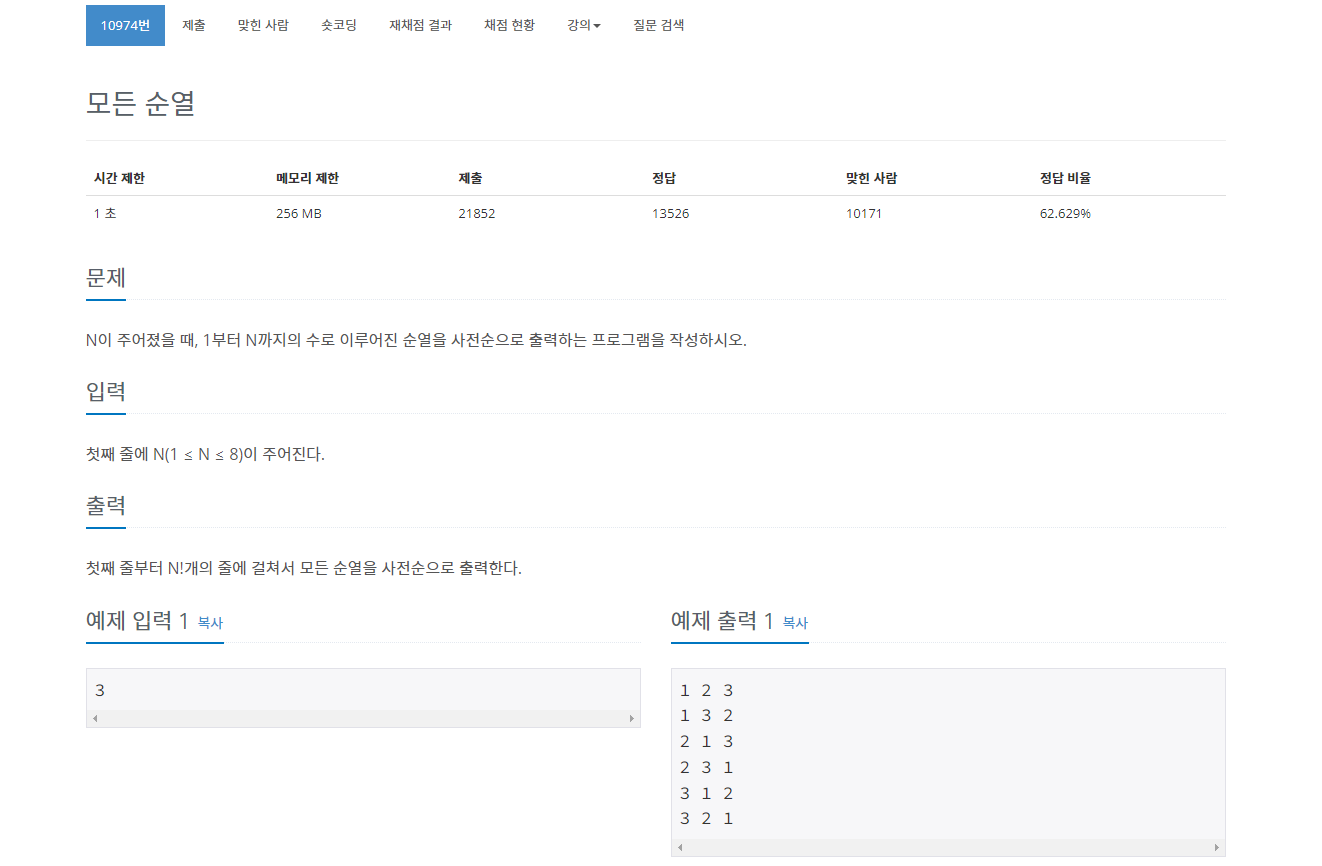
나의 풀이

N = int(input())
import itertools
nums = []
for i in range(1, N+1):
    nums.append(str(i))

li = list(map(' '.join, itertools.permutations(nums))) 
# map(함수, 리스트 or 튜플): 리스트나 튜플의 요소를 지정된 함수로 처리

for i in range(len(li)):
    print(li[i])

1. itertools의 순열을 활용하였다. itertools.permutation을 이용하면 반복문 없이도 순열을 구할 수 있다.

2. map함수와 join을 통해 순열을 '공백 한칸'을 기준으로 합쳤고, 이를 list함수로 터뜨렸다.

3. 그 후 리스트의 요소들을 차례차례 출력하였다

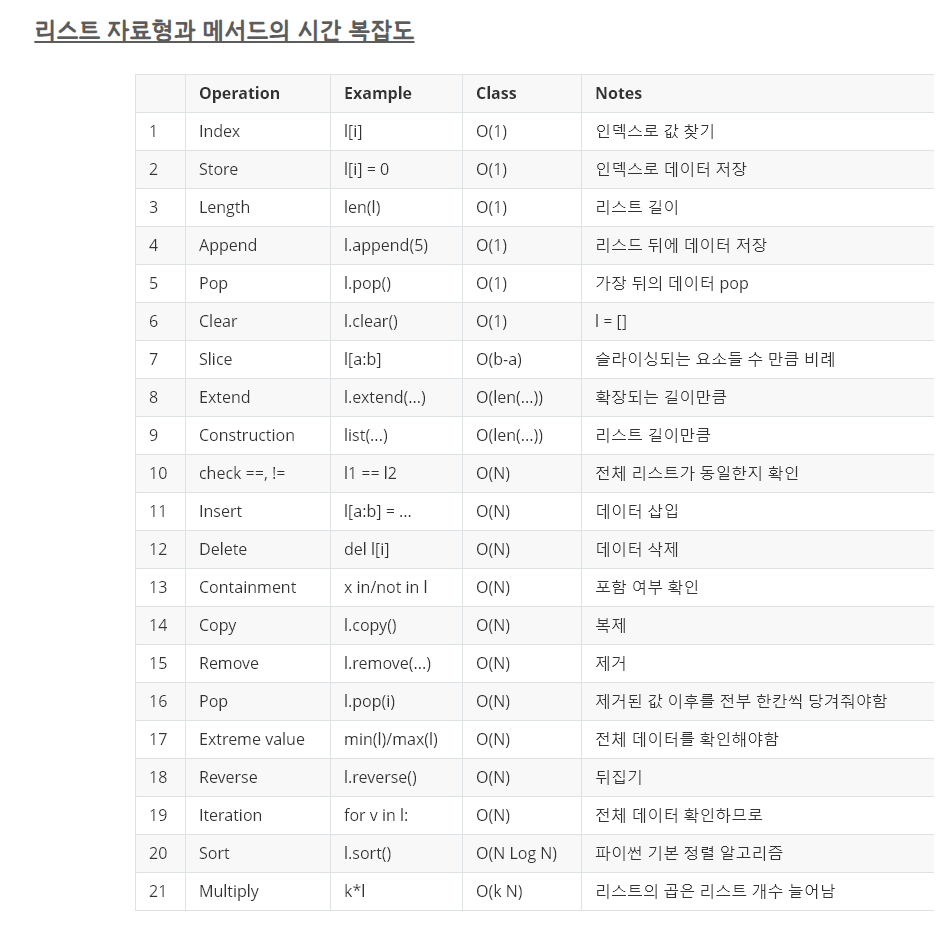
4. 자료구조로 리스트를 활용하였고, '모든 순열'이라는 것에서 힌트를 얻어 itertools의 permutation을 그대로 가져다 썼다. 공간복잡도는 32884KB, 시간복잡도는 O(n)(전체 데이터를 확인하므로)

5. O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(2^n) < O(n!)

2. 백준 11653 소인수분해

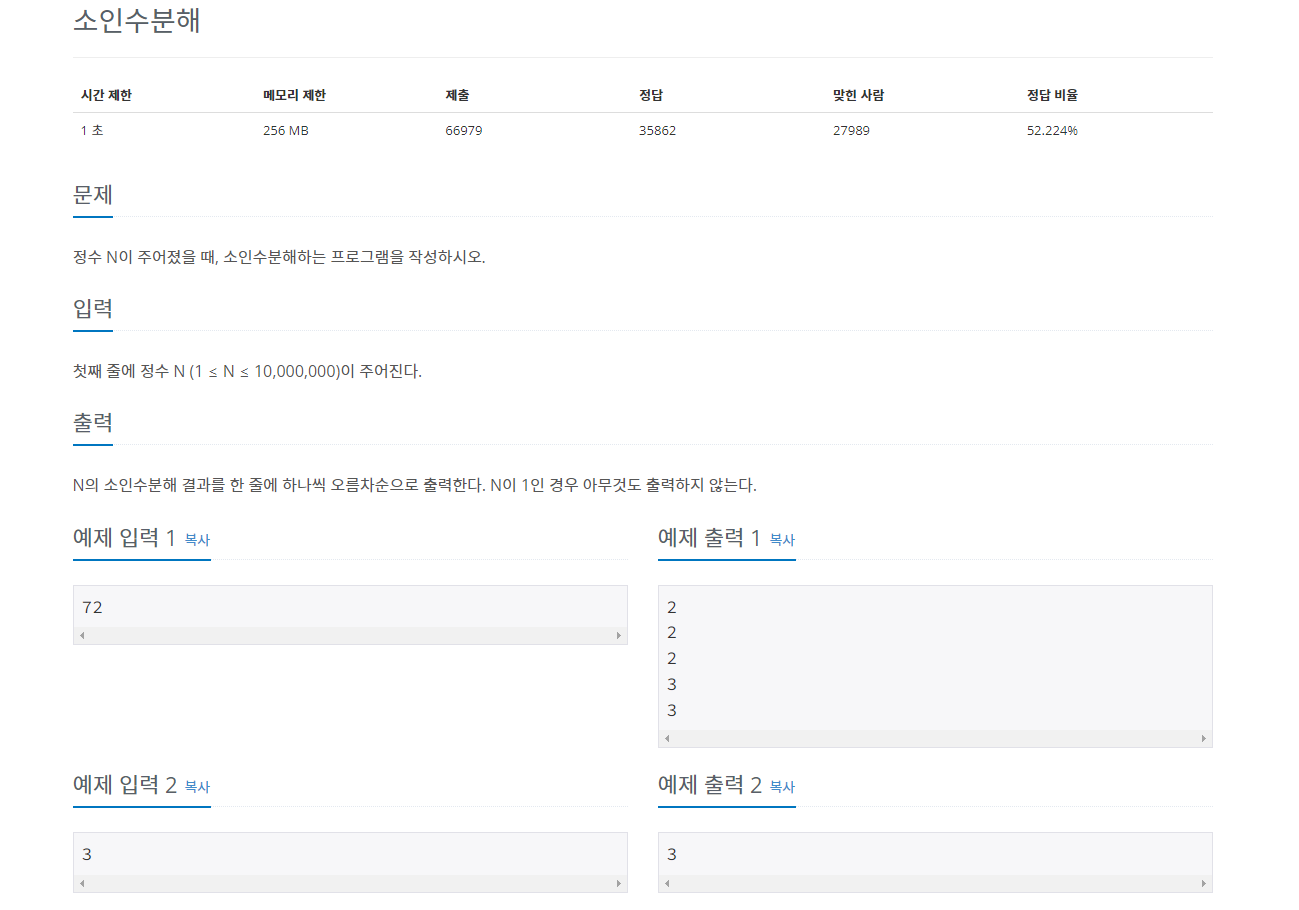
나의 풀이

N = int(input())
a = 2
if N == 1:
    print("")
else:
    while a <=N:
        if N%a == 0:
            print(a)
            N = N // a
        else:
            a +=1

1. N이 1인 경우, 그리고 그렇지 않은 경우로 구분하였다.

2. 알고리즘: 선형시간 알고리즘

3. 소인수 분해시 나누어떨어지는 수만 나타낸다는 점에서 힌트를 얻었다.

4. 시간 복잡도: O(n) (전부 검사하므로)

5. 공간 복잡도: 30840KB

3. 백준 1929 소수 구하기

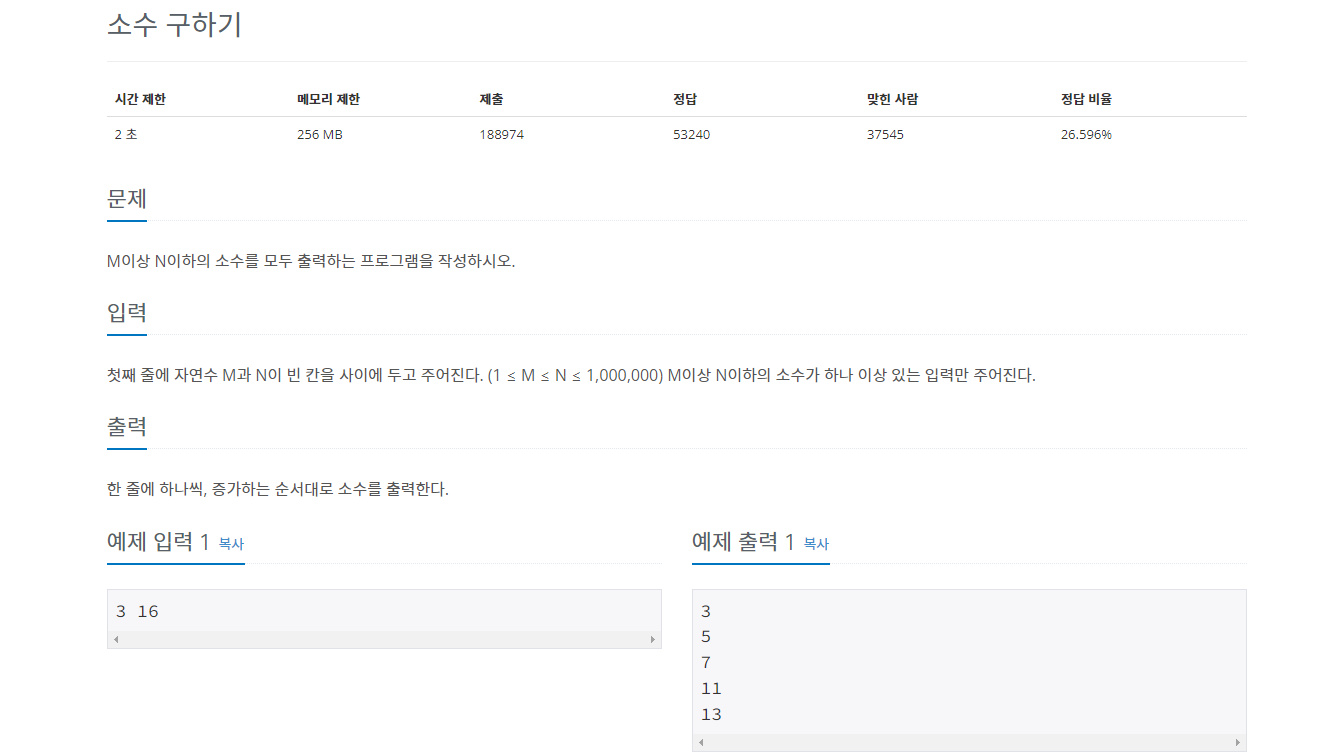
나의 풀이

m, n = map(int, input().split()) 
# 두 개의 인자를 입력 받아 정수로 집어넣는 방법
# (map과 split의 활용. 입력 받은 두 문자를 쪼개 리스트화 한 후, 그 리스트의 요소들을 map함수와 int 인자를 통해 각각 정수화하여 m,n에 대입)

def isprime(m, n):
  n += 1                            # for문 사용을 위한 n += 1
  prime = [True] * n                # n개의 [True]가 있는 리스트 생성
  for i in range(2, int(n**0.5)+1): # n의 제곱근까지만 검사
    if prime[i]:                    # prime[i]가 True일때
      for j in range(2*i, n, i):    # prime 내 i의 배수들을 False로 변환
        prime[j] = False

  for i in range(m, n):
    if i > 1 and prime[i] == True:  # 1 이상이면서 남은 소수들을 출력
      print(i)

isprime(m, n)

1. 알고리즘: 에라토스테네스의 체(일정 범위내 수열에서 배수들을 제거해 소수만 남기기)

2. 공간복잡도: 38512KB

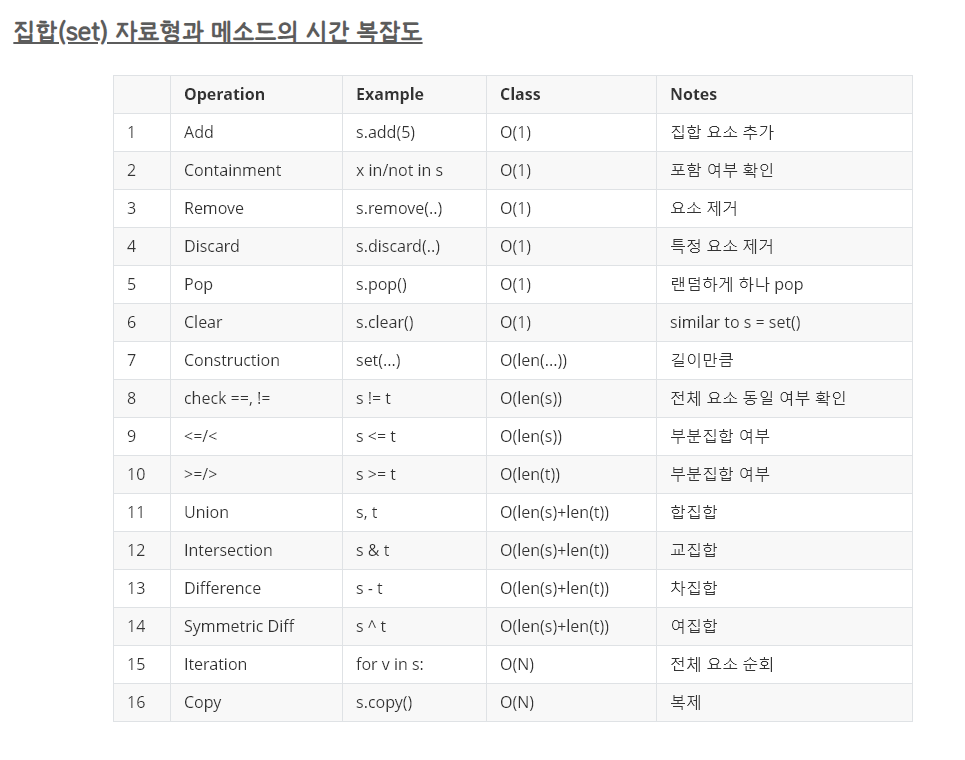
3. 자료구조로 리스트를 활용

4. 에라토스테네스의 체

: https://terms.naver.com/entry.naver?docId=1179083&cid=40942&categoryId=32204

4. 백준 2748 피보나치 수 2

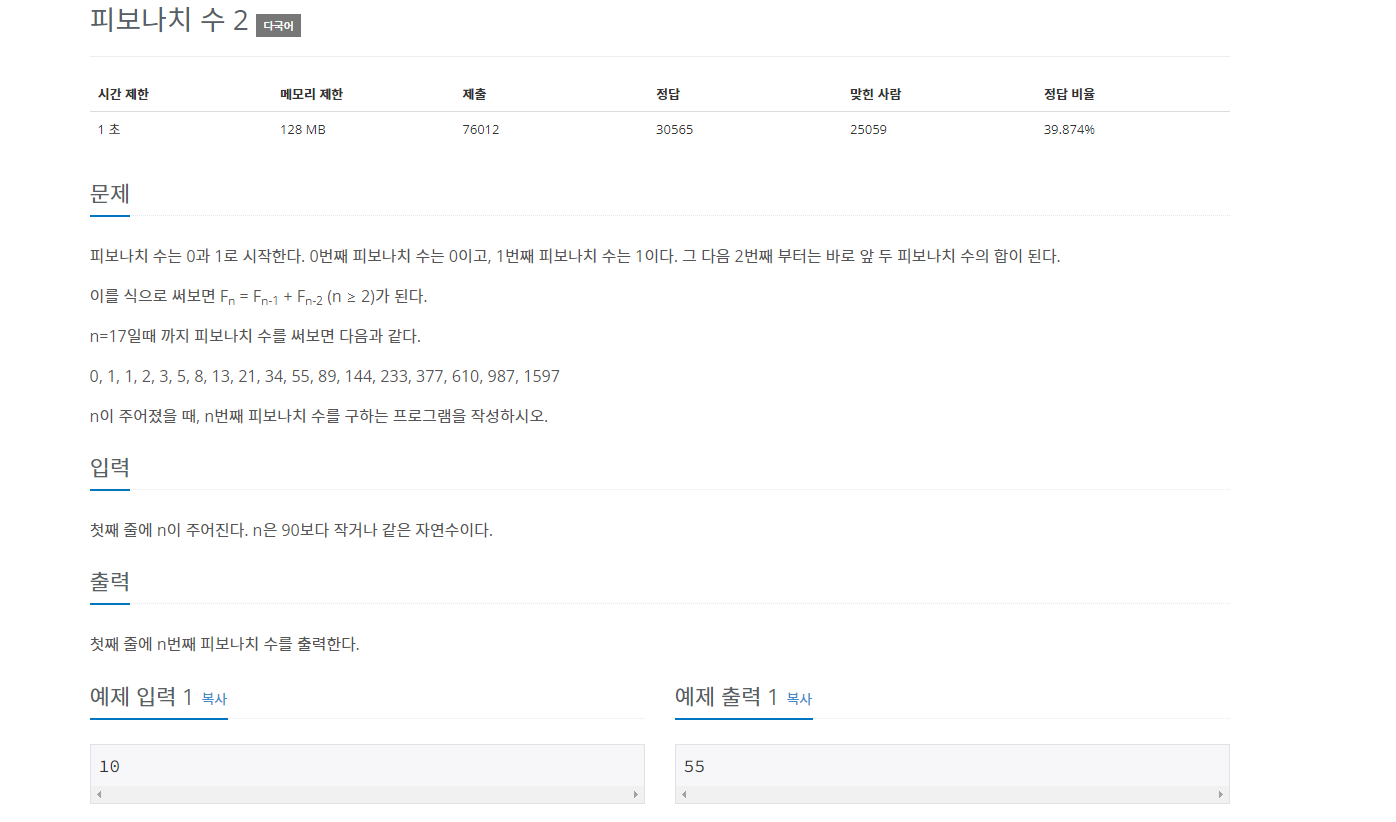
나의 풀이

n = int(input())

a = 0
b = 1
if n <0:
    print(-1)
elif n == 0: 
    print(0)
elif n == 1:
    print(1)
else:
    for i in range(1, n):
        a, b = b, b + a # n-2 번째 항과 n-1 번째 항의 합이 n번째 항이므로 이를 영리하게 활용한다. n-2번째 항과 n-1번째 항을 n-1번째 항과 n 번째 항으로 최신화 시켜준다.
    print(b)

(1) 문제번호: 2748 피보나치 수 2

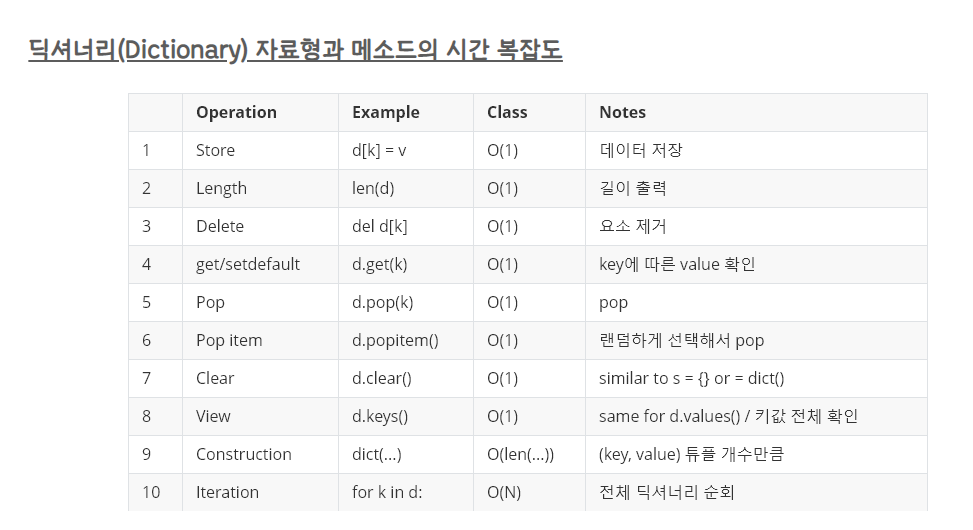
(2) 사용한 자료구조: 튜플

(3) 문제의 실마리: n-2 번째 항과 n-1 번째 항의 합이 n번째 항

-> n-2번째 항과 n-1번째 항을 n-1번째 항과 n 번째 항(n-2번째 항 + n-1번째 항)으로 최신화 시켜준다.

(4) 시간복잡도: O(2^n)

(5) 공간복잡도: 30840 KB

5. 백준 8393 합

나의 풀이

재귀함수 방식

n = int(input())
def sum(n):
    if n<=1:
        return n
    else:
        return n + sum(n-1)
print(sum(n))

for 문 활용(iterative)

n = int(input())
a = 0
for i in range(1, n+1):
    a += i
print(a)

분할법

N = int(input())
def sum_for_divide_conquer(N):
    def generate(n):
        if n == 1:
            return 1
        elif n % 2 == 1:
            return n + generate(n-1)
        else:
            return generate(n // 2) * 2 + (n ** 2) // 4
    return generate(N)
print(sum_for_divide_conquer(N))