목차
1. 관계 데이터 모델의 개념
2. 무결성 제약조건
3. 관계대수
-
관계 데이터 모델의 개념
-
릴레이션
-
릴레이션 스키마와 인스턴스
-
릴레이션의 특징
릴레이션
◆ 릴레이션(realtaion) : 행과 열로 구성된 테이블

첫 번째 행(1, 축구의 역사, 굿스포츠, 7000)의 경우 네 개의 집합에서 각각 원소 한 개씩 선택하여 만들어진것으로 이 원소들이 관계를 맺고 있다.
◆ 관계(realationship)
1. 릴레이션 내에서 생성되는 관계 : 릴레이션 내 데이터들의 관계
2. 릴레이션 간에 생성되는 관계 : 릴레이션 간의 관계
릴레이션 스키마와 인스턴스
◆ 스키마의 요소
• 속성(attribute) : 릴레이션 스키마의 열
• 도메인(domain) : 속성이 가질 수 있는 값들의 집합(예를들면 속성이 길이면 속성 값으로 사용자가 지정한cm,m등 만 들어올 수 있다. 또는 속성이 성별이면 속성 값으로 남, 여만 올 수 있다.)
• 차수(degree) : 속성의 개수
◆ 스키마의 표현
• 릴레이션 이름(속성1; 도메인1, 속성2: 도메인2, 속성3: 도메인3, ...)
EX) 도서(도서번호, 도서이름, 출판사, 가격)
◆ 인스턴스 요소
• 튜플(tuple) : 릴레이션의 행 -> 튜플이 가지는 속성의 개수를 릴레이션 스키마의 차우와 동일하고, 릴레이션 내의 모든 튜플들은 서로 중복되지 않아야 한다.
• 카디날리티(cardinality) : 튜플의 수
릴레이션의 특징
◆ 속성은 단일 값을 가진다. / 애트리뷰트의 원자성
• 각 속성의 값은 도메인에 정의된 값만을 가지며 그 값은 모두 단일 값이여야 함.
◆ 속성은 순서는 상관없다. / 애트리뷰트의 무 순서성
• 속성의 순서가 달라도 릴레이션 스키마는 같음.
◆ 릴레이션 내의 중복된 튜플은 허용하지 않는다. / 튜플의 유일성
• 튜플의 순서가 달라도 같은 릴레이션이다. 관계 데이터 모델의 튜플은 실제적인 값을 가지고 있으며 이 값은 시간이 지남에 따라 데이터의 삭제, 수정, 삽입에 따라 순서가 바뀔 수 있음.
◇ 관계 데이터 모델
• 관계 데이터 모델은 데이터를 2차원 테이블 형태인 릴레이션으로 포현함.
무결성 제약조건
- 키
- 무결성 제약조건
- 무결성 제약조건의 수행
◇ 키 (Key)
• 특정 투플을 식별 할 때 사용하는 속성 혹은 속성의 집합임.
• 릴레이션은 중복된 튜플을 허용하지 않기 떄문에 각각의 튜플에 포함된 속성들 중 어느 하나(혹은 하나 이상)은 값이 달라져야 한다.
• 키는 릴레이션 간의 관계를 맺는데도 사용됨.
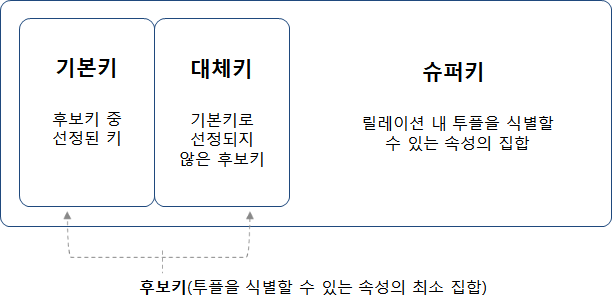
◇ 슈퍼키 (Super Key)
• 튜플을 유일하게 식별할 수 있는 하나의 속성 혹은 속성의 집합
- 튜플을 유일하게 식별할 수 있는 값이면 모두 슈퍼키가 될 수 있다.
◇ 후보키 (Candidate Key)
• 튜플을 유일하게 식별할 수 있는 속성의 최소 집합
• 2개 이상의 속성으로 이루어진 키를 복합키(composite key)라고 함
◇ 기본키 (Primary Key)
• 여러 후보키 중 하나를 선정하여 대표로 삼는 키
• 후보키가 하나뿐이라면 그 후보키를 기본키로 사용하면 되고 여러 개라면 릴레이션의 특성을 반영하여 하나를 선택하면 됨.
※ 기본키 선정 시 고려사항
• 릴레이션 내 튜플을 식별할 수 있는 고유한 값을 가져야 함.
• NULL 값은 허용하지 않음.
• 향후 키를 사용하는 데 있어서 문제 발생 소지가 없어야 함.
◆ 릴레이션 스키마를 표현할 때 기본키는 밑줄을 그어 표시함
• 릴레이션 이름(속성1, 속성2, ... 속성N)
ex) 고객(고객번호, 이름, 주민번호, 주소, 핸드폰)
◇ 대리키
◆ 기본키가 보안을 요하거나, 여러 개의 속성으로 구성되어 복잡하거나, 마땅한 기본키가 없을 때는 일련번호 같은 가상의 속성을 만들어 기본키로 삼는 경우가 있음. 이러한 키를 대리키(surrogate key) 혹은 인조키(artificial key)라고 함.
◆ 대리키는 DBMS나 관련 소프트웨어에서 임의로 생성하는 값으로 사용자가 직관적으로 그 값의 의미를 알 수 없음.
◇ 대체키 (alternate Key)
◆ 대체키는 기본키로 선정되지 않은 후보키(나머지)를 말함.
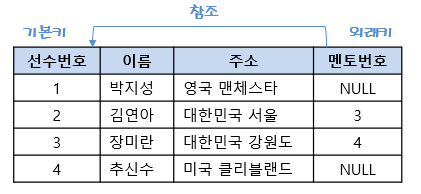
◇ 외래키 (foreign key)
◆ 외래키의 특징
• 관계 데이터 모델의 릴레이션 간의 관계를 표현함
• 다른 릴레이션의 기본키를 참조하는 속성임
• 참조하고(외래키) 참조되는(기본키) 양쪽 릴레이션의 도메인은 서로 같아야함.
• 참조되는(기본키) 값이 변경되면 참조하는(외래키) 값도 변경됨.
• NULL 값과 중복 값 등이 허용됨.
• 자기 자신의 기본키를 참조하는 외래키도 가능함.
• 외래키가 기본키의 일부가 될 수 있음.
자기 자신의 기본키를 참조하는 외래키도 가능하다
-> 외래키 사용 시 참조하는 릴레이션과 참조되는 릴레이션이 꼭 다른 릴레이션일 필요는 없다.
즉 자기 자신의 기본키를 참조할 수도 있다.
키 요약
무결성 제약조건
◆ 데이터 무결성(integrity)은 데이터 베이스에 저장된 데이터의 일관성과 정확성을 지키는 것을 말한다.
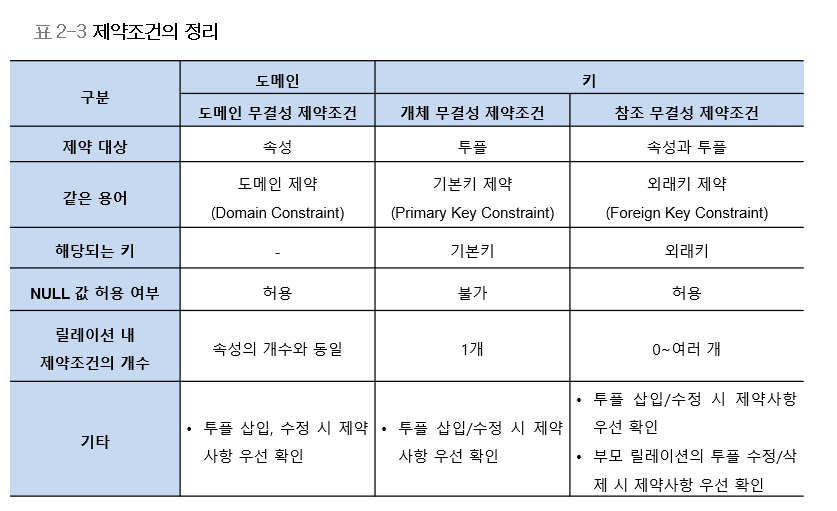
1. 도메인 무결성 제약조건
• 도메인 제약이라고도 하며, 릴레이션 내의 튜플들이 각 속성의 도메인에 지정된 값만을 가져야 한다는 조건
2. 개체 무결성 제약조건
• 기본키 제약이라고도 하며, 릴레이션의 기본키를 지정하고 그에 따른 무결성 원칙 즉,
3. 참조 무결성 제약조건
• 외래키 제약이라고도 하며, 릴레이션 간의 참조 관계를 선언하는 제약조건이다. 자식 릴레이션의 외래키는 부모 릴레이션의 기본키와 도메인이 동일해야 하며, 자식 릴레이션의 값이 변경될 때 부모 릴레이션의 제약을 받는다.
개체 무결성 제약조건
- 삽입 : 기본키 값이 같으면 삽입이 금지된다.
- 수정 : 기본키 값이 같거나 NULL로도 수정이 금지된다.
- 삭제 : 특별한 확인이 필요하지 않으며 즉시 수행한다.
참조 무결성 제약조건
- 삽입
학과(부모 릴레이션) : 튜플 삽입한 후 수행하면 정상적으로 진행된다.
학생(자식 릴레이션) : 참조받는 테이블에 외래키 값이 없으면 삽입이 금지된다.
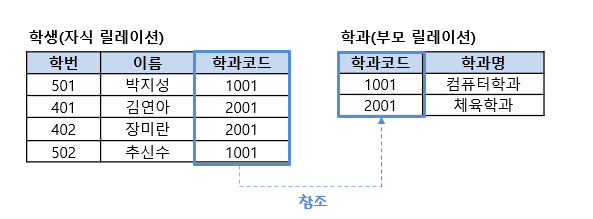
좀 더 자세히 설명하자면
학생 릴레이션에 새로운 투플을 삽입하려고 했을 때 DBMS는 먼저 도메인 무결성 제약조건을 확인한 후 개체 무결성 제약조건에 위배되는 값이 없는지 확인한다. 그리고 나서 학과코드 값이 학과 릴레이션의 기본키에 존재하는지 확인한다. 학생 릴레이션에 투플 (601, 박세리, 3001)을 삽입하려고 했을 때 학번 601은 들어갈 수 있지만 학과코드 3001은 들어갈 수 가 없으므로 수행이 거부된다. 만약 참조하는 학과코드가 NULL값을 허용 했다면 (601, 박세리, NULL) 값을 넣어 수행할 수는 있다.
- 삭제
학과(부모 릴레이션) : 참조하는 테이블을 같이 삭제할 수 있어서 금지하거나 다른 추가 작업이 필요하다.
학생(자식 릴레이션) : 바로 삭제 가능하다. - 수정
삭제와 삽입 명령이 연속해서 수행됨.
부모 릴레이션의 수정이 일어날 경우 삭제 옵션에 따라 처리된 후 문제가 없으면 다시 삽입 제약 조건에 따라 처리된다.
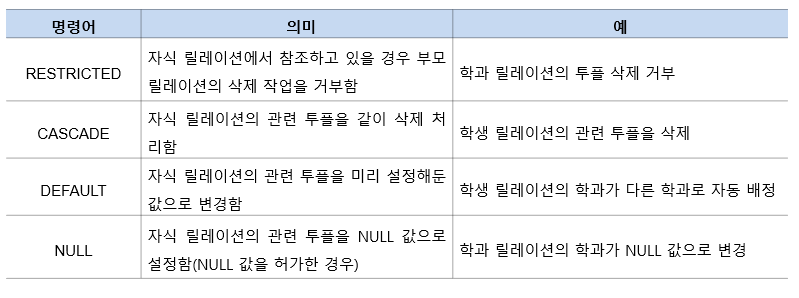
참조 무결성 제약조건의 옵션(부모 릴레이션에서 튜플을 삭제할 경우)
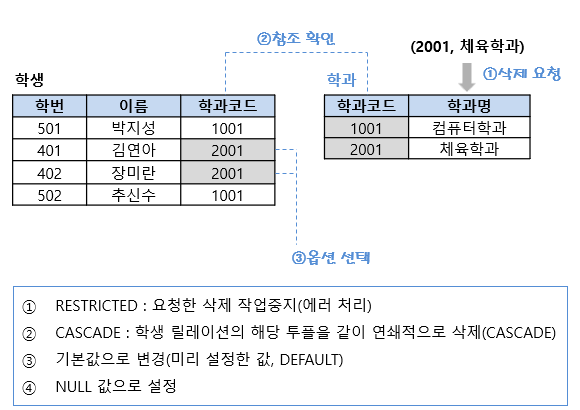
참조 무결성 제약조건에서 부모 릴레이션의 튜플을 삭제할 경우
관계대수
- 관계대수
- 셀렉션과 프로젝션
- 집합연산
- 조인
- 디비전
관계대수
◆ 관계대수
• 릴레이션에서 원하는 결과를 얻기 위해 수학의 대수와 같은 연산을 이용하여 질의하는 방법을 기술하는 언어
◆ 관계대수와 관계해석
• 관계대수 : 어떤 데이터를 어떻게 찾는지에 대한 처리 절차를 명시하는 절차적인 언어이며, DBMS 내부의 처리 언어로 사용됨.
• 관계해석 : 어떤 데이터를 찾는지만 명시하는 선언적인 언어로 관계대수와 함께 관계 DBMS의 표준 언어인 SQL의 이론적인 기반을 제공함.
-> 관계대수와 관계해석은 모두 관계 데이터 모델의 중요한 언어이며 실제 동일한 표현 능력을 가지고 있음.
◇ 관계의 수학적 의미
릴레이션의 현실 세계 적용
예) 학번={2,4}, 과목={데이터베이스, 자료구조, 프로그래밍}일 때, 두 집합의 카르티전 프로덕트인 학번X과목은 학번 원소와 과목 원소의 순서쌍의 집합이다. 즉, 학번X과목={(2, 데이터베이스), (2, 자료구조), (2, 프로그래밍), (4, 데이터베이스), (4, 자료구조), (4, 프로그래밍)}을 말한다.
그래서 수강 릴레이션의 {(2, 데이터베이스), (2, 자료구조), (4, 프로그래밍)}은 카티전 프로덕트 학번×과목의 부분집합으로 하나의 릴레이션 인스턴스라고 할 수 있다.
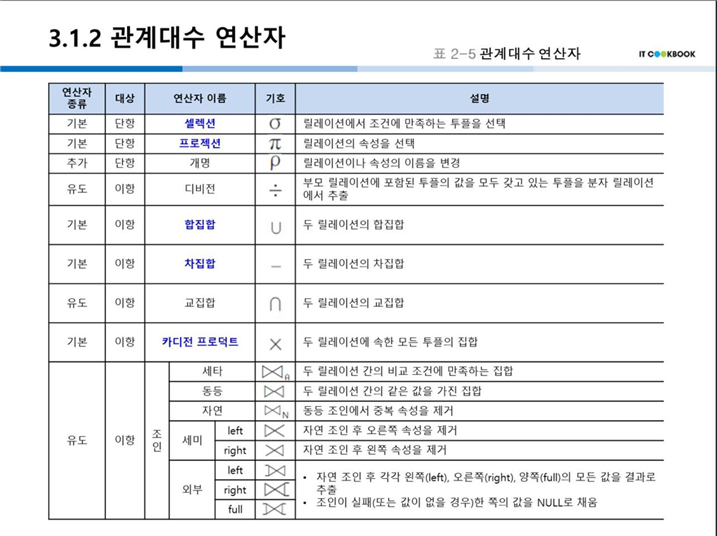
◇ 관계대수 연산자
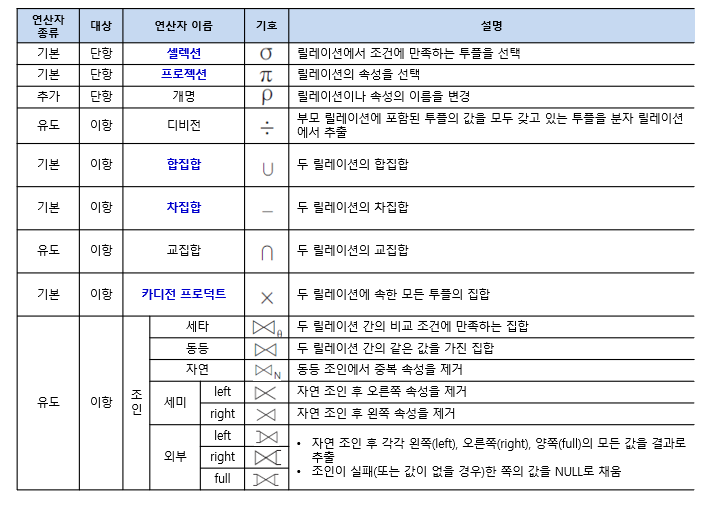
◇ 관계대수식
■ 관계대수식
• 관계대수는 릴레이션 간 연산을 통해 결과 릴레이션을 찾는 절차를 기술한 언어로, 이 연산을 수행하기 위한 식을 관계대수식이라고 함. 관계대수식은 대상이 되는 릴레이션과 연산자로 구성되며, 결과는 릴레이션으로 반환됨. 반환된 릴레이션은 릴레이션의 모든 특징을 따름.
• 단항 연산자 : 연산자<조건> 릴레이션
• 이항 연산자 : 릴레이션1 연산자<조건> 릴레이션2
◇ 셀렉션(selection)
◆ 릴레이션의 튜플을 추출하기 위한 연산임. 하나의 릴레이션을 대상으로 하는 단항 연산자이며, 찾고자 하는 튜플의 조건(predicate)을 명시하고 그 조건에 만족하는 튜플을 반환함
◆ 형식 : σ<조건> (R) (R은 릴레이션, σ는 그리스 문자이며 대문자는 Σ)
◇ 프로젝션(projection)
◆ 릴레이션의 속성을 추출하기 위한 연산으로 단항 연산자임.
◇ 합집합
◆ 두 개의 릴레이션을 향하여 하나의 릴레이션을 반환함. 이 때 두 개의 릴레이션은 서로 같은 속성 순서와 도메인을 가져야 함. 형식 : R ∪ S
◇ 교집합
◆ 합병 가능한 두 릴레이션을 대상으로 하며, 두 릴레이션이 공통으로 가지고 있는 튜플을 반환함.
◆ 형식 : R ∩ S
◇ 차집합
◆ 첫 번째 릴레이션에는 속하고 두 번째 릴레이션에는 속하지 않는 튜플을 반환함.
◆ 형식 : R ∙ S
◇ 카티전 프로덕트
◆ 두 릴레이션을 연결시켜 하나로 합칠 때 사용함. 결과 릴레이션은 첫 번쨰 릴레이션의 오른쪽에 두 번째 릴레이션의 모든 튜플을 순서대로 배열하여 반환함. 결과 릴레이션의 차수는 두 릴레이션의 차수의 합이며, 카디널리티는 두 릴레이션의 카디널리티의 곱임.
◆ 형식 : R × S
◇ 조인(join)
◆ 두 릴레이션의 공통 속성을 기준으로 속성 값이 같이 튜플의 수평으로 결합하는 연산임. 조인을 후생하기 위해서는 두 릴레이션의 조인에 참여하는 속성이 서로 동일한 도메인으로 구성되어야 함. 조인 연산의 결과는 공통 속성의 속성 값이 동일한 튜플만을 반환함.
◆ 형식 : R ⋈c S = σc(R×S) (R과 S는 릴레이션, c는 조인 조건)
◆ 조인 연산의 구분
• 기본 연산 : 세타조인(⋈A), 동등조인(⋈), 자연조인(⋈N)
• 확장된 조인 연산 : 세미조인(⋉,⋊), 외부조인( ⟖, ⟕, ⟗ )
◇ 세타 조인(theta join, θ)
• 조인에 참여하는 두 릴레이션의 공통 속성을 기준으로 속성 값이 같은 튜플을 수평으로 결합하는 연산임. 조인을 수행하기 위해서는 참여하는 속성이 서로 동일한 도메인으로 구성되어야 함. 조인연산의 결과는 공통 속성의 속성 값이 동일한 튜플만을 반환함.
• 세타조인의 조건은 { =, ≠, ≤, ≥, <, > } 중 하나가 됨.
• 형식 : R⋈(r 조건 S) S ( R과 S는 릴레이션이며 r은 R의 속성, s 는 S의 속성)
◇ 동등조인(equi join)
• 세타조인에서 = 연산자를 사용한 조인을 말함. 보통 조인 연산이라고 하면 동등조인을 지칭함
• 형식 : R⋈(r=s)S
◇ 자연조인(natural join)
• 동등조인에서 조인에 참여한 속성이 두 번 나오지 않도록 두 번째 속성을 제거한 결과를 반환함.
• 형식 : R⋈N(r, s) S
◇ 외부조인과 세미조인
◆ 외부조인(outer join)
• 자연조인 시 조인에 실패한 튜플을 모두 보여주되 값이 없는 대응 속성에는 NULL 값을 채워서 반환
• 모든 속성을 보여주는 기준 릴레이션 위치에 따라(left) 외부조인, 오른쪽(right) 외부조인, 완전(full) 외부 조인으로 나뉨
형식 : 왼쪽(left) 외부조인 - R ⟕(r,s) S
완전(full) 외부조인 - R ⟗(r,s) S
오른쪽(right) 외부조인 - R ⟗(r,s) S
◆ 세미조인(semi join)
• 자연조인을 한 후 두 릴레이션 중 한쪽 릴레이션의 결과만 반환하며, 기호에서 닫힌 쪽 릴레이션의 튜플만 반환함.
• 형식 : R⋉(r,s) S
◇ 디비전(division) ★★
◆ 릴레이션의 속성 값의 집합으로 연산을 수행함.
• 형식 : R ÷ S
◇ 관계대수 연산자 정리(표)