목차
- 벨먼-포드 알고리즘이란?
- 알고리즘 사용 예시
- 불가능한 예시
- 시간 복잡도
1. 벨먼-포드 알고리즘이란?
가중 유향 그래프(edge에 방향과 가중치가 있는 그래프)의 최단 경로 문제를 푸는 알고리즘 입니다.
이전에 살펴본 다익스트라 알고리즘과 비슷하지만 벨먼 포드의 경우 가중치에 음수가 들어갈 수 있습니다.
2. 알고리즘 사용 예시
아래와 같은 그래프로 벨먼 포드 알고리즘의 예시를 들어보겠습니다.
우선 시작 노드와 살펴볼 edge의 순서를 정합니다. 또한 시작 노드를 제외한 다른 노드의 초기값은 INF(무한대)로 설정합니다.
주어진 edge의 순서대로 살펴 봅니다.
시작점의 값이 INF라면 값의 수정이 이루어지지 않습니다.
그렇기 때문에 (B, C)부터 (D, E)까지 수정이 이루어지지 않습니다.
(A, B)의 경우 A = 0이기 때문에 살펴보아야 합니다.
(B의 값) 과 (A의 값 + edge의 가중치)를 비교해서 낮은 값을 B의 값으로 수정합니다.
INF와 -2 를 비교하면 -2가 작기 때문에 B의 값은 -2가 됩나다.
이런 과정을 정해두었던 순서의 끝까지 진행합니다.
이러한 과정을 정점의 갯수만큼 반복하는 것이 벨먼-포드 알고리즘입니다.
예시의 경우 5번을 반복하게 됩니다.
두번쩨 순서에서 값들이 수정된 결과를 살펴보겠습니다.
(B, C)의 경우 3과 1을 비교하므로 1로 수정됩니다.
(D, C)의 경우 1과 5를 비교합니다. 기존의 값이 더 낮기 때문에 수정되지 않습니다.
주어진 수서를 2번째로 끝까지 진행하면 다음과 같은 모습이 됩니다.
이론대로 한다면 5번까지 반복해야 하지만 3번째부터는 수정되는 값이 없으니 여기까지 보여드리겠습니다.
3. 불가능한 예시
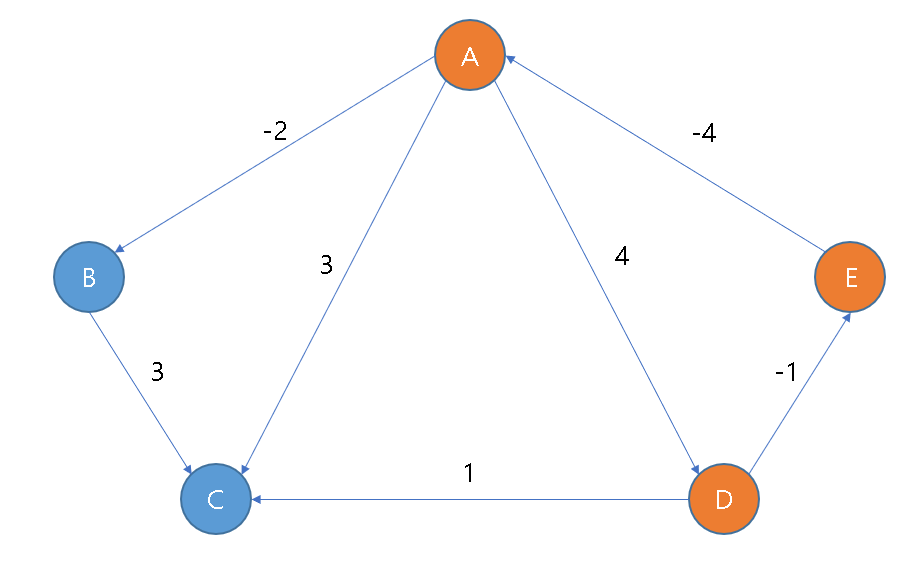
위 그래프는 앞서 보여드렸던 예시의 가중치를 일부 변경한 것입니다.
표시된 부분은 사이클(cycle)이 형성됩니다.
앞서 보여드렸던 예시로 사이클 자체가 문제가 아닌 것을 알수 있습니다.
이번 예시에서 달라진 점은 사이클의 가중치를 합치면 음수가 나온다는 것입니다.
이렇게 될 경우 끊임없이 값이 수정됩니다.
이러한 경우 값을 구할 수 없습니다.
4. 시간 복잡도
순서대로 edge 전체를 정점만큼 반복합니다.
edge를 E, 정점의 갯수를 V라고 할 때
O(E * V)입니다.
