0과 1로 숫자를 표현하는 방법
정보의 단위
비트(bit)
컴퓨터는 0과 1밖에 이해하지 못하는데 이를 통해 나타내는 가장 작은 정보의 단위를 비트(bit)라고 한다.
비트를 전구에 빗대어 생각해 보면 0은 꺼짐, 1은 켜짐의 상태로 표현할 수 있다.
그렇다면 2비트는 몇 개의 정보를 표현할 수 있을까?
(켜짐, 켜짐), (켜짐, 꺼짐), (꺼짐, 꺼짐), (꺼짐, 켜짐) 총 4가지 상태를 표현할 수 있다.
따라서 n비트는 2^n만큼의 정보를 표현할 수 있다.
비트보다 큰 단위로는 바이트, 킬로바이트, 메가바이트, 기가바이트 등이 있는데 각각의 크기는 아래와 같다.
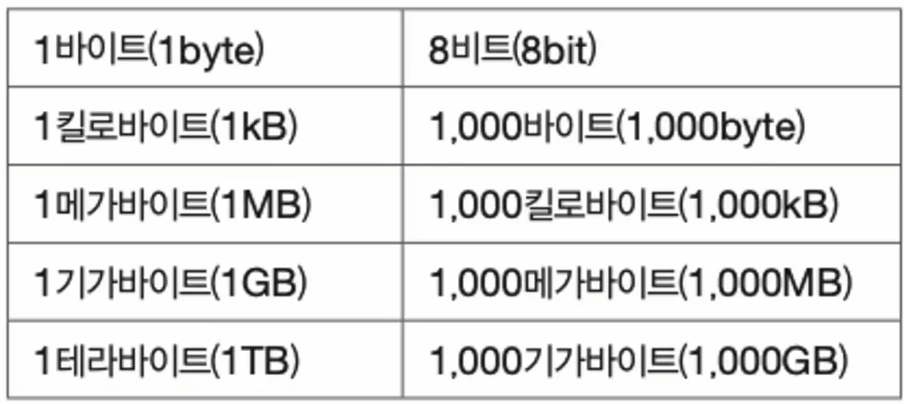
1바이트만 8비트이며, 다음 단위로 넘어갈때마다 이전 단위에 1000을 곱한 값이된다.
1024를 곱해야하지 않냐고 물어볼 수 있지만, 엄밀하게 말해서 1024개씩 묶어 표현하는 단위는 KiB, MiB, GiB등으로 다른 단위이다.
이진법
수학에서 0과 1로 모든 숫자를 표현하는 방법을 이진법이라고 한다.
우리가 일상생활에서 사용하는 것은 십진법으로 9까지 세고, 그 다음을 셀 때 자리를 올림하는데, 이진법도 마찬가지로 1을 넘어가는 시점에 자리를 올림한다.
이진법으로 표현한 수를 이진수, 십진법으로 표현한 수를 십진수라고 한다.
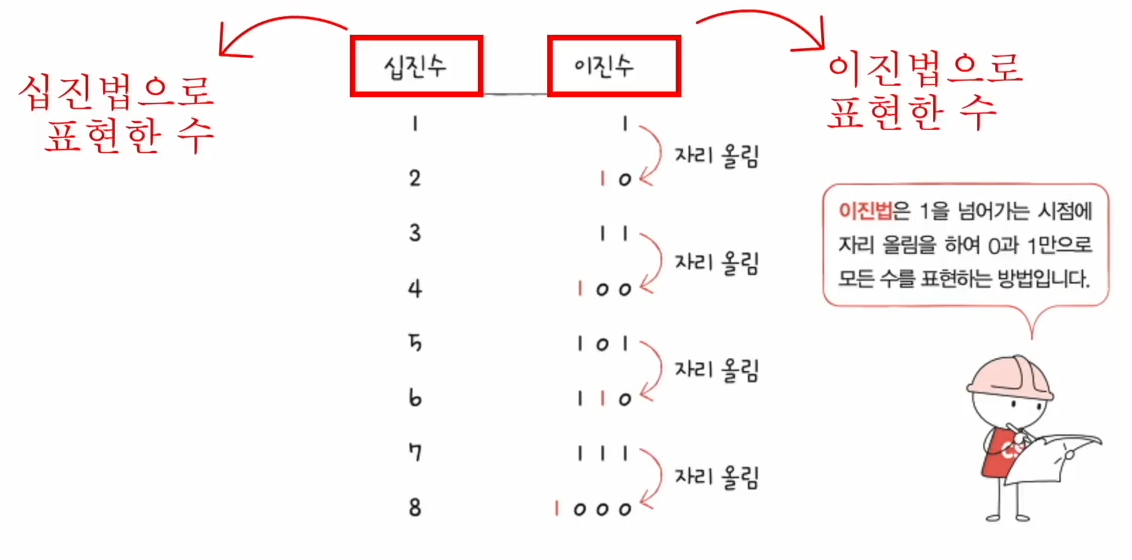
이진수는 표기할 때 해당 숫자가 이진수인 것을 알아볼 수 있도록 1100(2) 이런식으로 표현을 해준다.
이진수의 음수 표현
십진수를 음수로 표현할 때는 단순하게 앞에 -만 붙여주면 되지만 컴퓨터는 0과 1만을 이해할 수 있기 때문에 -부호를 붙일 수 없다.
따라서 0과 1만으로 음수를 나타내야 하는데, 이때 가장 널리 사용되는 방법은 2의 보수를 구해 이 값을 음수로 간주하는 것이다.
2의 보수
어떤 수를 그보다 큰 2^n에서 뺀 값을 의미한다.
예를들어 11(2)보다 큰 100(2)에서 11(2)을 뺀 01(2)이 11(2)의 보수이다.
간단하게 계산하는 방법은 모든 0과 1을 뒤집고 1을 더하면 된다.
예를들어 11(2)의 0과 1을 뒤집으면 00(2), 1을 더해주면 01(2)이 된다.
하지만 이렇게 구한 보수 01(2)이 1을 의미하는지 -3을 의미하는지 어떻게 구분할까?
이진수만 보고 구분하는 것은 불가능하며, 따라서 컴퓨터에서는 어떤 수가 양수인지 음수인지 구분하기 위해 플래그를 사용한다.
십육진법
이진법으로 모든 숫자를 표현할수는 있지만, 0과 1만으로 모든 숫자를 표현하기 때문에 숫자의 길이가 너무 길어진다는 단점이 있다.
그래서 데이터를 표현할 때 이진법 이외에 십육진법도 자주 사용한다.
십육진법은 숫자가 15를 넘어갈 때 자리올림을 하는 방식으로, 십진수 10~15까지를 각각 A,B,C,D,E,F로 표현한다.
이러한 십육진법을 사용하는 이유는 이진법과의 변환이 매우 쉽기 때문이다.
십육진수를 이진수로 변환하기
십육진수는 한 글자당 16종류의 숫자를 표현할 수 있기 때문에 이진수로 표현하기 위해서는 4비트가 필요하다(2^4=16)
십육진수를 이진수로 변환하는 방법 중 하나는 십육진수 한 글자를 4비트의 이진수로 간주하는 것이다.
예를들어 1A2B(16)라는 십육진수가 있을 때 각 숫자 1(16), A(16), 2(16), B(16)를 이진수로 표현하면 0001(2), 1010(2), 0010(2), 1011(2)이며, 해당 숫자를 이어붙인 값 0001101000101011(2)이 1A2B(16)를 이진수로 표현한 값이다.
이진수를 십육진수로 변환하기
반대로 이진수를 십육진수로 변환할 때는 이진수 숫자를 4개씩 끊고, 4개 숫자를 하나의 십육진수로 변환 뒤 이어붙이면 된다.
예를들어 11010101(2)을 4개씩 끊으면 1101(2), 0101(2)이고 이는 각각 D(16), 5(16)이므로 이어붙인 D5(16)가 변환된 값이다.
0과 1로 문자를 표현하는 방법
문자 집합과 인코딩
아스키 코드
EUC-KR
유니코드와 UTF-8
