
지난 시간에 이어서
오늘은 자료 구조 중 tree와 graph에 대해
공부했다.
tree는 이전에도 collection에 대해 공부할 때
배운적이 있는데,
그때의 tree보다 좀 더 깊게 들어갔고,
언제 사용하는지도 고민해봤다.
tree
tree에 대해 처음 배울 때에는
root, 자식 node, 부모 node, leaf node에 대해서만 알고 넘어갔는데,
사실 tree를 표현하는데에 여러 용어가 존재한다.
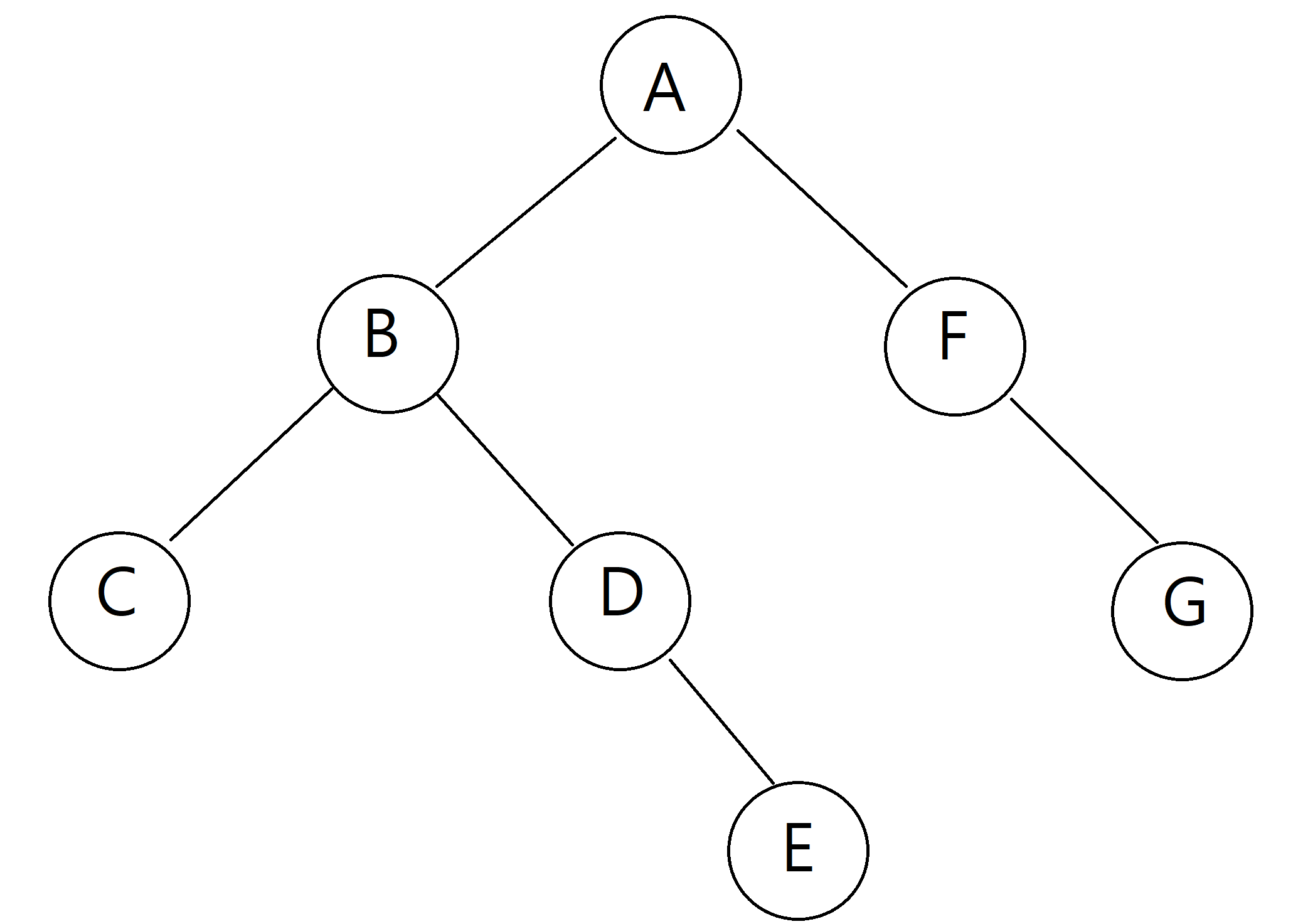
depth
root로부터 특정 node까지의 깊이를 표현하는 것이다.
depth0 = {A}
depth1 = {B, F}
depth2 = {D, G}
depth3 = {E}level
level은 depth와 같은 개념이지만, level은 1부터 시작한다.
level 1 = {A}, level 2 = {B, F}, level 3=...height
height는 말그대로 높이로 depth와 level과는 다르게
leaf node를 기준점으로 heigth를 정한다.
위의 그림에서 C, D, G는 같은 depth(level)이지만,
heigth는 다르다. C와 G는 leaf node지만,
D는 자식 node를 갖기 때문이다.
그렇다면 B node의 heigth는 어떻게 정할까?
자식 node 중 가장 heigth가 높은 node의 heigth+1이다.
따라서
height0 = {C, E, G}
height1 = {D, F}
height2 = {B}
hheight3 = {A}장점?
tree는 이진 탐색 트리나 후에 배울 힙과 같은 다양한 형태로
사용되며 정렬과 탐색에 용이하다.
삽입이나 삭제 시,
부모 node와 자식 node만 수정하면 되기 때문에 해당 과정이 쉽다.
이진 탐색 트리
모든 왼쪽 자식 node의 값이 root나 부모 node의 값보다 작고,
모든 오른쪽 자식 node의 값이 root나 부모 node의 값보다 큰 값을 가진다.
어떠한 값을 탐색하고 자 할 때 그 값이 비교할 노드의 값보다 작으면 왼쪽으로, 크면 오른쪽으로 움직여 값을 찾는 방식으로 최악의 경우 트리의 heigth만큼 탐색을 진행한다.
예를 들어,
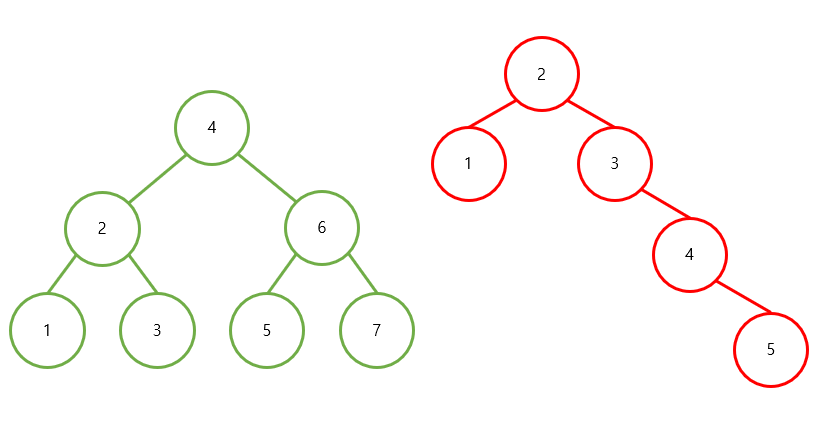
위 경우 왼쪽 tree는 노드의 개수가 7개, height는 2
오른쪽 tree는 노드의 개수가 5개, height가 3으로
만약 5를 찾는다고 하면 노드의 개수가 많더라도
height가 더 작은 왼쪽 tree의 탐색 시간이 더 짧을 것이다.
따라서 node가 한 쪽으로 몰린다면,
탐색하는 데 시간이 걸릴 수 있다.
이진 탐색 트리에서 노드의 삭제
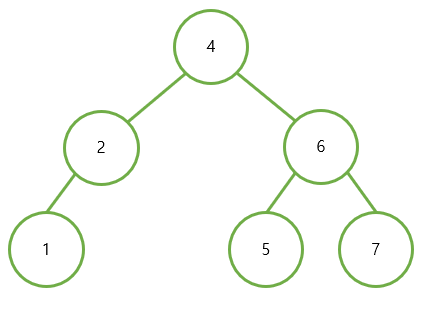
1. leaf node 삭제
1이나 5, 7처럼 삭제 대상이 leaf node라면 그냥 삭제하면 된다.
2. 한 개의 자식 node가 존재
node 2를 삭제한다면, node 2의 부모 node인 4와
자식 node인 1을 연결해 주면 된다.
3. 두 개의 자식 node가 존재

node 6을 삭제한다면, 두 자식 node 중 작은 node (5)를 찾고,
해당 node (5)를 6과 교환 한다.
