99클럽 코테 스터디 22일차 TIL / [LeetCode] Maximal Rectangle

오늘의 학습 키워드

---

DP

문제

---

https://leetcode.com/problems/maximal-rectangle/

• 플랫폼: LeetCode
• 문제명: Maximal Rectangle
• 난이도: Hard

풀이

---

class Solution {
    public int maximalRectangle(char[][] matrix) {
        int[] heights = new int[matrix[0].length];
        int answer = 0;

        for(int row=0; row<matrix.length; row++) {
            for(int col=0; col<matrix[0].length; col++) {
                if(matrix[row][col] == '1') {
                    heights[col]++;
                } else {
                    heights[col] = 0;
                }

                int rightCol = col;
                int curHeight = matrix.length;

                for(int leftCol=col; leftCol>=0; leftCol--) { 
                    int height = heights[leftCol];
                    int width = rightCol - leftCol + 1;

                    if(height == 0) {
                        break;
                    }

                    curHeight = Math.min(curHeight, height);
                    answer = Math.max(answer, curHeight * width);
                }
            }
        }

        return answer;
    }
}

접근

• 행렬의 현재 row에서 가지는 높이를 저장하는 heights 배열을 만들면 O(n^3) 풀이가 가능합니다.
  • 행렬의 모든 좌표 탐색 → O(n^2)
  • 현재 좌표에서 가능한 직사각형의 최대 크기 구하기 → O(n)

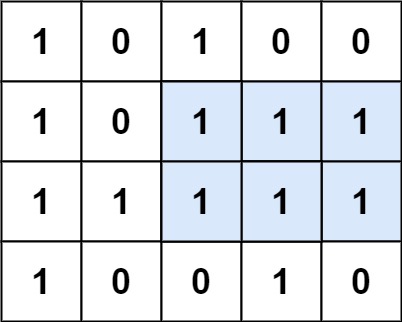이미지 출처: https://leetcode.com/problems/maximal-rectangle/description/

• heights 배열은 다음과 같은 형태로 채워지게 됩니다.

  	0번째 컬럼	1번째 컬럼	2번째 컬럼	3번째 컬럼	4번째 컬럼
  0번째 행	1	0	1	0	0
  1번째 행	2	0	2	1	1
  2번째 행	3	1	3	2	2
  3번째 행	4	0	0	3	0

• 로직
  1. 좌표를 순회하며 heights 배열을 채웁니다.
  2. 현재 좌표에서 가질 수 있는 직사각형 크기의 최댓값을 계산합니다.
     1. 직사각형의 width
        현재 좌표를 기준으로 왼쪽 방향으로 이동하면서, 가능한 직사각형의 가로 길이를 구합니다.
        즉, 직사각형의 오른쪽 컬럼은 항상 현재 좌표로 고정되고, 왼쪽 컬럼을 하나씩 늘려가는 것입니다.
     2. 직사각형의 height
        heights 배열에 저장된 높이를 그대로 사용하다가 더 작은 높이가 나온다면 해당 값을 height로 설정합니다.
        높이가 0인 경우에는 더이상 직사각형을 만들 수 없으므로 2번 과정을 종료하고 다시 1번으로 돌아갑니다.

소요 시간

1시간 30분