벡터(Vector), 행렬(Matrix) , 텐서(Tensor)

1차원으로 구성된 값을 우리는 벡터(Vecter)라고 한다. 2차원으로 구성된 값을 행렬(Matrix)라고 한다. 그리고 3차원이 되면 우리는 텐서(Tensor)라고 부른다. 4차원은 3차원의 텐서를 위로 쌓아 올린 모습으로 상상 할 수 있다.

2D Tensor

|t| = (Batch size, dim)

3D Tensor - 비전 분야에서의

|t| = (batch size, width, height)

3D Tensor - NLP 분야에서의

|t| = (batch size, length, dim)

Linear Regression(선형 회귀)

'Regression toward the mean'

Hypothesis

H(x) = Wx + b
이때 x와 곱해지는 W를 가중치(Weight)라고 하며, b를 편향(bias)이라고 한다.
간략화 하면 H(x) = Wx

cost (=lose/error)

H(x) - y
'오차 = 실제값 -예측값'으로 오차값이 음수가 나오는 경우가 생긴다. 따라서 비용 함수를 구할 때 각 오차값을 제곱해준 뒤에 전부 더한다.

비용 함수 Cost(W,b)

간략화한 비용함수

Cost(W,b)를 최소가 되게 만드는 W와 b를 구하면 훈련 데이터를 가장 잘 나타내는 직선을 구할 수 있다.

Gradient descent algorithm (경사 하강법 - 옵티마이저)

기울기 W가 무한대로 커지면 커질 수록 cost의 값 또한 무한대로 커지고, 반대로 기울기 W가 무한대로 작아져도 cost의 값은 무한대로 커진다. 위의 그래프에서 cost가 가장 작을 때는 맨 아래의 볼록한 부분이다. 기계가 해야할 일은 cost가 가장 최소값을 가지게 하는 W를 찾는 일이므로, 맨 아래의 볼록한 부분의 W의 값을 찾아야 한다. 기계는 임의의 초기값 W값을 정한 뒤에, 맨 아래의 볼록한 부분을 향해 점차 W의 값을 수정해나간다.

• 기울기가 음수일 때 : W의 값이 증가
  W:= W−α×(음수기울기) = W + α×(양수기울기)
• 기울기가 양수일 때 : W의 값이 감소
  W:= W−α×(양수기울기)

결과적으로 기울기가 0인 방향으로 W의 값이 조정된다.
여기서 α값은 learning rate로 W 값을 변경할 때, 얼마나 크게 변경할지를 결정한다.

기울기를 구할 때 미분을 위해 비용함수를 수정한다.

경사하강법의 주의점

주변에 대해서는 가장 낮은 지점(local minimum)일 수 있지만 전체에 대해서는 가장 낮은 지점(global minimum)이 아닐 수 있다.

Multivariable Linear regression(다중 선형 회귀)

변수가 많을 수록 가중치가 많아진다. 따라서 행렬(Matrix)를 사용한다.

행렬 연산은 변수의 개수와 관계 없이 같은 식은 사용하므로 행렬 연산은 식을 간단하게 해줄 뿐만 아니라 다수의 샘플의 병렬 연산이므로 속도의 이점을 가진다.
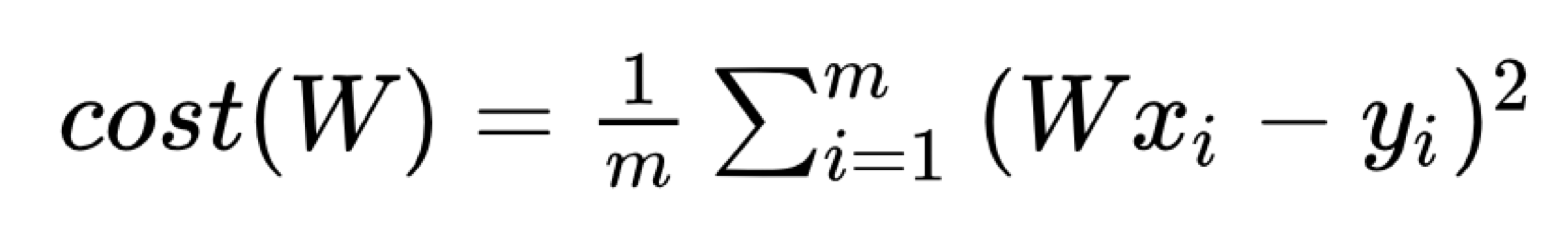
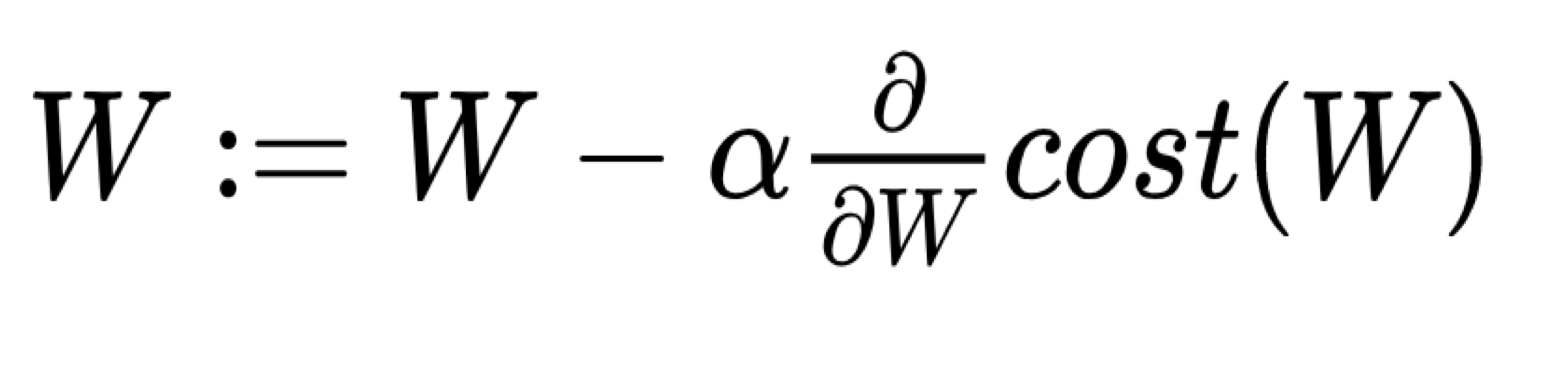